Кто хорошо может определять и делить.
Платон Процесс ознакомления с новыми объектами, объединенными понятием, в нашем исследовании назван деятельностью «введение понятия» [12, 13, 15 и др.]. Это один из основных видов деятельности учащихся на уроке, имеющем дело с научными понятиями. Поскольку процесс введения понятия рассматривается нами как деятельность, то его структура должна быть адекватна структуре понятия «деятельность». Покажем, как структура категории «деятельность», приведенная выше (см. рис. 5, с. 22), конкретизируется в деятельности введения понятия (ДВП). Источником возникновения ДВП является потребность во введении в изучение нового для учащихся математического объекта. Иллюстрацию необходимости изучения нового объекта, выделение его из ранее известных, введение понятия, его обозначающего, обеспечивает проблемная ситуация. Для мотивации изучения понятия и обозначения арифметического квадратного корня может быть задание на решение следующих квадратных уравнений:
(рис. 21) показывает, что его корни существуют, как и в уравнениях (1), (2). Более того, они противоположны. Но назвать эти числа, записать их учащиеся не могут, т.к. соответствующих знаний у них пока еще нет. Возникает осознание потребности в новых знаниях, в расширении понятия числа, во введении обозначения Понимание необходимости изучения нового объекта сопровождается постановкой общей цели — ввести в изучение дисциплины новое понятие. Ознакомление с понятием сопровождается введением термина и символа, принятого в науке для краткой записи; изучением определения нового понятия; формированием умения распознавать объекты, входящие в объем нового понятия, и применять определение понятия в дальнейшем обучении. Термин или символ, как правило, позволяют показать историю возникновения и развития понятия. Появляется возможность рассказать учащимся об ученых, впервые использующих данное понятие; о научных дискуссиях по тому или иному вопросу; о нравственных качествах людей, посвятивших свою жизнь математическим исследованиям. Для одной категории учащихся исторические экскурсы усиливают мотивацию их познавательной деятельности, для других школьников не менее значимо убедиться в существовании нового математического объекта. Например, в случае с понятием арифметического квадратного корня из семи полезно доказать, что не существует рационального числа, квадрат которого равен семи. Если мотивация учащихся состоялась, то начинается деятельность по введению нового понятия. В нашем примере изучения понятия арифметического квадратного корня рассмотрение объектов определенного рода (например квадратных уравнений: х 2 = 5; х 2 = 7; х 2 = 8; х 2 = 11) показывает существование чисел, являющихся квадратами других (рис. 21). Однако назвать точное значение х можно было только в случае, если число, стоящее в правой части уравнения, представимо в виде точного квадрата. В других случаях задача оставалась без ответа. У учащихся возникает потребность к изучению понятия арифметического квадратного корня из любого неотрицательного числа, и они готовы поставить (принять) цели, которые задают действия ДВП: · определение понятия; · выведение следствий из определения; · подведение под понятие; · классификация (или обобщение) понятия. Эта структура деятельности «введение понятия» обусловлена сущностью ее предмета — понятия как категории логики (см. выше п. 3.1, с. 47). Основные положения реализации деятельностного подхода при введении понятия раскрыты и аргументированы выше (см. с. 70-71). Поэтому на основе вышеизложенного продолжим описание осуществления ДВП на примере введения понятия арифметического квадратного корня. Уравнения (1) – (4), решение которых были использованы для мотивации учащихся (см. с. 76), могут быть использованы в качестве упражнений для введения определения понятия конструктивным приемом (рис. 21). При решении уравнения
После усвоения термина и обозначения перед учащимися ставится цель (или они сами ставят ее): сформулировать определение понятия «арифметический квадратный корень из числа а». После текстовой формулировки определения учащимися и при уточнении ее (по необходимости) учителем следует запись на математическом языке, сопоставление двух форм записи определения, в котором происходит усвоение формулировки определения: Определение. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. Действие определения понятия выполнено. Формулировка определения является началом его усвоения, которое продолжается осуществлением действия подведения под понятие. Подведение под понятие реализуется решением задач с дидактической функцией [83] — заданий на формирование видовых отличий определения понятия. Примеров таких задач, как правило, достаточно в учебниках. Например, на подведение под понятие арифметического квадратного корня, т.е. на усвоение видовых отличий: 1) 1. Докажите, что число 5 является (–5 не является) арифметическим квадратным корнем из 25 [4, с. 66]. 2. Докажите, что 3. Вычислите: 4. Найдите значение переменной, при котором Число таких задач по каждой теме в учебниках различно. Так, в учебнике геометрии А.В. Погорелова они практически отсутствуют, что обязывает учителя дополнять локальную систему задач. Усвоение понятия арифметического квадратного корня из числа а продолжается изучением определения. Использование наглядной формулировки (символической записи определения) помогает учащимся выявить другие существенные свойства понятия, отличные от определяющих: ( Следствие 1. Следствие 2. Эти первые «открытия» теории арифметического квадратного корня учащиеся могут сделать самостоятельно, более того, они смогут дать обоснование истинности утверждений. Традиционный подход «дать учащимся всю теорию полностью в готовом виде, в том числе и эти свойства», утрачивает значение. Таким образом, выполняя действие «выведение следствий из определения», учащиеся узнают существенные свойства понятия, не вошедшие в определение, то есть продолжается усвоение содержания понятия. Каждое из следствий очень важно в дальнейшем изучении темы. Однако в действующих школьных учебниках [4] изучение свойства, например, ( Задание 1. Вычислить: Задание 2. Сократить дробь: Следствия определения, пополняющие содержание понятия новым фактом, а также понятие подкоренного выражения должны быть усвоены при изучении понятия арифметического квадратного корня, как того требуют дидактические принципы. Если на усвоение первого следствия определения арифметического квадратного корня из числа а ( Отметим, что следствия определений понятий в курсе алгебры представлены в учебниках практически для каждого понятия, хотя так не именуются. Например, a В действующих школьных учебниках алгебры принят индуктивный подход к изложению теории. Поэтому чаще всего, осуществляя ДВП, выполняется действие обобщения понятия, раскрывающее перспективы изучения предмета. Так, при изучении арифметического квадратного корня осуществляется обобщение понятия: Наконец, отметим, что классификация (или обобщение) понятия как действие, направленное на овладение понятием, в контексте с введением понятия в методике преподавания математики часто не выделяется [20, 40, 67, 68, 75, 76, 113, 126]. 4.2.2. Структура действий деятельности «введение понятия» Введение нового понятия как деятельность состоится в результате выполнения четырех действий, каждое из которых соответствует частной цели, определенной мотивом ДВП: 1) выделить свойства изучаемого понятия, с помощью которых объекты, входящие в объем нового понятия, будут отличаться от других математических объектов; 2) научиться распознавать, принадлежит ли предъявленный объект объему введенного понятия (действие «подведение под понятие»); 3) соотнести введенное понятие (его видовые отличия) с ранее изученными фактами (вывести следствия из определения); 4) включить изученное определение в систему имеющихся знаний: выявить частные виды нового понятия или установить, видом какого понятия является вновь изученное понятие (действие «классификация» или «обобщение понятия»). Первая цель задает действие определения понятия. Его структуру составляют операции: · выделение родового понятия и видовых отличий (реализуемое приемом отбора или конструктивным приемом [100, с. 15–16]); · введение термина и обозначения (если оно предусмотрено); · формулировка определения в текстовой форме; · формулировка определения в знаковой форме (символическая запись определения). Положение о формировании познавательного инструментария учащихся [98] (см. с. 33) требует, чтобы для осуществления действия определения понятия ученик знал его смысл[13] и операциональный состав. При этом мы придерживаемся сформулированных выше описаний сущности категорий «содержание понятия», «определение понятия», логической операции «определение понятия», «определяемое понятие», «определяющее понятие» (см. с. 53). Сформированность познавательного инструментария учащихся означает, что при самостоятельном изучении определения понятия ученик должен вычленять в тексте: · определяемое понятие (термин), его обозначение; · определяющее понятие (родовое понятие и видовые отличия, представленные различными логическими конструкциями[14]); · символическую запись определения. В случае отсутствия символической записи определения понятия ученик должен уметь выполнить ее. Для формирования осознанного изучения школьниками определения нового для них понятия, для воспитания познавательной привычки учащихся работать подобным образом следует в классе во фронтальной работе четко[15] организовывать ДВП, осуществляя рефлексию действия определения понятия. Итак, знание сущности действия определение понятия раскрывает учащимся логическую структуру определения, ориентирует на выделение определяющих свойств понятия (основного содержания понятия). Это дает возможность учащимся самостоятельно формулировать определение понятия в текстовой и знаковой форме, способствует осознанию места изучаемого понятия в системе других понятий, позволяет качественно применять его при доказательстве теорем и решении задач. Вторая частная цель ДВП задает действие (прием логического мышления) подведение объекта под понятие. Действие, посредством которого обосновывается, что некоторый объект или отношение принадлежит соответственно множеству объектов или отношений, составляющих объем данного понятия, называется подведением под понятие [68 ] и является одним из основных действий деятельности введения понятия. Овладение этим действием относится к одной из ключевых компетенций школьника [142] и является составляющей математической компетентности. Это общее действие (общий вид деятельности, как отмечает Н.Ф. Талызина) формируется у учащихся начальной школы [128]. Его структуру составляют операции: · выделение понятия, под который следует подвести данный объект, его определяющих признаков; · выделение понятия, которому принадлежит объект, актуализация его определяющих признаков; · сравнение совокупности определяющих признаков понятия, которому принадлежит объект (множество А), и совокупности определяющих признаков понятия, под которое подводится объект (множество В); · установление отношения включения между множествами А и В: · вывод о принадлежности объекта объему данного понятия. Очевидно, что первые две из выделенных операций действия «подведение объекта под понятие» основаны на овладении действием «определение понятия», являются применением определения в новой ситуации. Это составляет проявление элементарного акта самостоятельности учащегося в деятельности. Свертывание мыслительных операций в действия, а действий — в деятельность у каждого ребенка происходит по-своему, сообразно его психическим особенностям [55]. Приведем интерпретацию действия «подведение под понятие» на примере степени с натуральным показателем. Выполнение действия предполагает осуществление умения выбрать из различных примеров те, которые являются степенью числа. Например, для подведения под понятие выражения 1) вспомнить (мысленно представить) определение степени с натуральным показателем[16], выделить его определяющие признаки: · «произведение n множителей», · «каждый из которых равен а»; 2) назвать понятие, к которому относится данный объект (выражение): произведение п множителей; 3) установить, имеет ли место включение множества определяющих признаков понятия степени с натуральным показателем во множество признаков, характеризующих данный объект; 4) на основе установленного факта В процессе решения задач и доказательствах теорем почти всегда приходится устанавливать, что данные объекты или отношения принадлежат объемам соответствующих понятий, т.е. выполнять действие «подведение под понятие» (см., например, шестой силлогизм доказательства свойства медианы, проведенной к основанию равнобедренного треугольника, с. 14). Третья частная цель ДВП (соотнести вновь введенное понятие, его видовые отличия с ранее изученными фактами) задает действие выведение следствий из определения понятия. Как показано выше, это действиеслужит «открытию» существенных свойств понятия, не включенных в формулировку определения. Его структуру составляют операции: · выделение каждого видового отличия в определении понятия (его определяющих признаков); · сделать вывод из факта, зафиксированного данным видовым отличием, включая его в систему имеющихся знаний или выполняя соотнесение с определяемым понятием. Так, выделение видового отличия арифметического квадратного корня: Включение определения изученного понятия в совокупность известных фактов служит основой для появления нового знания. Например, следствием определения параллелограмма является свойство суммы углов, прилежащих к данной стороне параллелограмма (их сумма равна 180º). Для получения этого факта достаточно применить свойство внутренних односторонних углов, образованных прямыми, содержащими параллельные стороны, и секущей — прямой, проходящей через смежную сторону. Следствием определения уравнения с одной переменной (неизвестной) (см. с. 59) являются понятия корня (решения) уравнения, области определения уравнения (области допустимых значений). Наконец, действие классификации понятия, способствующее расширению математического кругозора учащихся, формированию представления об объеме понятия, осуществляется следующими операциями: · выбор основания классификации (признака, по которому выполняется деление множества объектов); · выполнение деления множества на подмножества (классы); · исследование возможности дальнейшего деления полученных классов. Это действие выполнятся как сразу после введения определения понятия, так и в ходе систематизации знаний о понятии. Например, с понятием «выражение» учащиеся знакомятся в начальной школе. Уже в пятом классе ученики могут приводить примеры следующих выражений: х + 5; 5 + 8; х + у = у + х; Опыт показывает, что, выбрав в качестве основания классификации признак «наличие переменной (буквы) в выражении», учащиеся приходят к одной из известных классификаций этого понятия [67] (конечно, в терминах, соответствующих уровню их знаний):
Рис. 24 Такие классификационные схемы, иллюстрируя многообразие видов данного понятия, показывают учащимся перспективу изучения предмета, с одной стороны, а с другой — обращение к ним способствует формированию системы знаний, представлений о родовых и видовых понятиях. Действие «классификация понятия» можно формировать у учащихся посредством заданий на установление общего признака объектов и заданий на деление множества объектов на подмножества, выделением основания классификации. Такие задания уже появляются в учебной литературе [130, 152], они характерны для учебников системы развивающего обучения Л.В. Занкова, используются в учебниках математики Г.В. Дорофеева, Л.Г. Петерсон [37, 38] и др.
|

 (1) Ответ:
(1) Ответ:  .
.
 (2) Ответ:
(2) Ответ:  .
.
 (3) Ответ: Ø.
(3) Ответ: Ø.
 (4) Ответ:
(4) Ответ:  .
Графическое решение последнего уравнения
.
Графическое решение последнего уравнения
 Рис. 21
Рис. 21
 . Аналогично может быть построено изучение понятия степени с натуральным показателем, логарифма числа (см. с. 19), а также многих других понятий школьного курса математики.
. Аналогично может быть построено изучение понятия степени с натуральным показателем, логарифма числа (см. с. 19), а также многих других понятий школьного курса математики. . Усвоение термина и обозначения реализуется на следующих примерах (1 –5):
. Усвоение термина и обозначения реализуется на следующих примерах (1 –5):

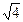 = 2. Ответ:
= 2. Ответ:  . Ответ:
. Ответ:  ,
,  . Ответ:
. Ответ:  .
4.
.
4.  ; Ответ:
; Ответ:  и т.п.
5.
и т.п.
5.  ; х =? Ответ:
; х =? Ответ:  .
.



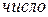 b:
b: 
 .
. в учебнике 14 заданий [4]. Приведем некоторые из них.
в учебнике 14 заданий [4]. Приведем некоторые из них. и т.п., еще три упражнения.
и т.п., еще три упражнения.
 (всего десять упражнений).
(всего десять упражнений). (
( и т.п.).
и т.п.). b:
b:  . Ответ на вопрос: «Какие выводы из определения можно сделать о значениях числа а?» будет первым следствием определения понятия [12]. Второе следствие учащиеся получают заменой b во втором определяющем свойстве на
. Ответ на вопрос: «Какие выводы из определения можно сделать о значениях числа а?» будет первым следствием определения понятия [12]. Второе следствие учащиеся получают заменой b во втором определяющем свойстве на  .
.
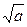 )2 = а явно не учитывает закономерностей процесса познания, реализации деятельностного подхода. В первую очередь это задачи на представление любого положительного числа в виде квадрата:
)2 = а явно не учитывает закономерностей процесса познания, реализации деятельностного подхода. В первую очередь это задачи на представление любого положительного числа в виде квадрата:  и т.п. Этот факт позволяет расширить круг задач линии тождественных преобразований выражений до изучения свойств арифметического квадратного корня. Содержанием дидактического материала учебника не обеспечено усвоение следствий определения: отсутствуют задания на нахождение значения выражений и упрощение выражений типа:
и т.п. Этот факт позволяет расширить круг задач линии тождественных преобразований выражений до изучения свойств арифметического квадратного корня. Содержанием дидактического материала учебника не обеспечено усвоение следствий определения: отсутствуют задания на нахождение значения выражений и упрощение выражений типа: ;
;  .
. и т.п.
и т.п. ;
;  » [4, с. 68]), то изучение второго следствия:
» [4, с. 68]), то изучение второго следствия:  , а значит, и овладение понятием
, а значит, и овладение понятием  не обеспечено системой упражнений [4] и др.
не обеспечено системой упражнений [4] и др. = b при b > 0, a > 0, a ≠ 1 — основное логарифмическое тождество является следствием определения логарифма (см. с. 41). Иначе обстоит дело с изучением следствий определений понятий в курсе геометрии. Так, следствием определения параллелограмма является свойство углов, прилежащих к одной его стороне, часто используемое при решении задач. Следствие определения трапеции — аналогичное свойство углов, прилежащих к ее боковой стороне. Следствием определения вписанного в окружность угла является утверждение о соответствии вписанному углу дуги окружности, на которую он опирается. Как было замечено выше, существенные свойства понятия — следствия определения, входят в содержание изучаемого понятия, могут быть «открыты» учащимися самостоятельно (под руководством учителя). Поэтому выполнение действия «выведение следствий определения» в структуре ДВП позволяет ученику: понять, как строится теория; получать опыт формулировки умозаключений, установления новых фактов в естественных, а не искусственно созданных условиях; развивать самостоятельность мышления, инициативу в познавательной деятельности; иметь эмоциональную поддержку в ходе обучения на разных этапах урока. Все эти факторы способствуют становлению ценностно-смысловой сферы личности, развитию мотивации учения.
= b при b > 0, a > 0, a ≠ 1 — основное логарифмическое тождество является следствием определения логарифма (см. с. 41). Иначе обстоит дело с изучением следствий определений понятий в курсе геометрии. Так, следствием определения параллелограмма является свойство углов, прилежащих к одной его стороне, часто используемое при решении задач. Следствие определения трапеции — аналогичное свойство углов, прилежащих к ее боковой стороне. Следствием определения вписанного в окружность угла является утверждение о соответствии вписанному углу дуги окружности, на которую он опирается. Как было замечено выше, существенные свойства понятия — следствия определения, входят в содержание изучаемого понятия, могут быть «открыты» учащимися самостоятельно (под руководством учителя). Поэтому выполнение действия «выведение следствий определения» в структуре ДВП позволяет ученику: понять, как строится теория; получать опыт формулировки умозаключений, установления новых фактов в естественных, а не искусственно созданных условиях; развивать самостоятельность мышления, инициативу в познавательной деятельности; иметь эмоциональную поддержку в ходе обучения на разных этапах урока. Все эти факторы способствуют становлению ценностно-смысловой сферы личности, развитию мотивации учения. Отметив, что в обозначении арифметического квадратного корня показатель корня — число 2 — не пишется, можно поставить на обсуждение вопросы: можно ли говорить о других видах арифметических корней, какие задачи приводят к этим понятиям? Ответы на эти вопросы иллюстрируют учащимся перспективу изучения предмета, суть развития математической теории.
Отметив, что в обозначении арифметического квадратного корня показатель корня — число 2 — не пишется, можно поставить на обсуждение вопросы: можно ли говорить о других видах арифметических корней, какие задачи приводят к этим понятиям? Ответы на эти вопросы иллюстрируют учащимся перспективу изучения предмета, суть развития математической теории. ;
; необходимо выполнить следующие операции:
необходимо выполнить следующие операции: сделать вывод о том, что данное произведение не является степенью числа.
сделать вывод о том, что данное произведение не является степенью числа.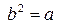 (см. с. 79), применение свойств неотрицательности квадрата числа и отношения равенства позволяют сделать вывод, во-первых, о неотрицательности значений подкоренного выражения а. Во-вторых, соотнесение с определяемым понятием:
(см. с. 79), применение свойств неотрицательности квадрата числа и отношения равенства позволяют сделать вывод, во-первых, о неотрицательности значений подкоренного выражения а. Во-вторых, соотнесение с определяемым понятием:  замена
замена  на
на  , дает важное тождество
, дает важное тождество  .
. ;
;  х > 3.
х > 3.



