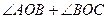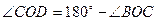Д. Гершель
Понятия являются главными составляющими любой науки, каждого учебного предмета. В нашем исследовании, исходящем из признания приоритета предмета познавательной деятельности в процессе обучения математике (с. 30), обеих его сторон (логико-операционной и содержательной), математическим понятиям отводится особое внимание. Обеспечение полноценного усвоения математических понятий — программное требование и одна из главных задач учителя. Обращение к школьной практике показывает, что «… эта задача решается не так успешно, как того требуют цели общеобразовательной школы» [128, с. 187]. Об этом свидетельствуют и результаты обучения (см. выше), а также многочисленные исследования, в частности Н.Ф. Талызиной. Главным недостатком школьного усвоения понятий издавна считается формализм, суть которого состоит в том, что учащиеся, правильно воспроизводя определения понятий, не умеют пользоваться ими в процессе решения задач и доказательстве утверждений. Если считать формулирование учеником определения понятия осознанием его содержания, то неумение пользоваться им при ориентировке в предметной действительности называется не иначе как формализмом в знаниях. До настоящего времени сохраняется главная причина этого явления. Мы разделяем мнение Н.Ф. Талызиной, что формализм в усвоении школьниками понятий (в том числе и математических) сохраняется ввиду отсутствия в обучении (в учебниках) ознакомления учащегося с логической структурой определения. Заучив огромное количество различных конкретных определений, ученик не может восстановить при необходимости забытое, «так как не знает структуры определений, не владеет правилами их построения» [128, с. 73]. Еще раз наглядно продемонстрируем роль понятий и их определений в доказательстве утверждения на примере одной из первых теорем геометрии: при изучении свойства вертикальных углов. Сначала представим определения развернутого угла и вертикальных углов, используемые в доказательстве. В текстовой формулировке выделены определяемое понятие, родовое понятие и видовые отличия. Приведена символическая запись этих определений.
Теорема о вертикальных углах имеет импликативную структуру:
Доказательство представим дедуктивным рассуждением, иллюстрирующим применение определений понятий. Сравнение приведенного доказательства с изложением этой теоремы в любом учебнике показывает, что определения понятий использованы не только на уровне термина, представления (образа), но с воспроизведением и полным выделением определяющих признаков. Это значит, что овладение понятием продолжается в ходе изучения его свойств, причем используется символическая запись определяющих признаков понятия.
Применение определения понятия в доказательстве, представленном дедуктивным рассуждением (табл. 3), актуализирует действие подведение под понятие, требует использования определения в новой ситуации. Многократное применение определения в развернутой форме, бесспорно, способствует сознательному, а не формальному его усвоению. Деятельностный подход к обучению при формировании понятий означает, что «понятие не может быть передано учащимся в готовом виде, они должны получить его сами, взаимодействуя с относящимися к нему предметами. … Определение задает как бы точку зрения — ориентировочную основу — для оценки предметов, с которыми взаимодействует обучаемый. … Такая реальная работа по оценке различных предметов постепенно создает в голове ученика адекватное понятие как обобщенный и абстрактный образ предметов данного класса» [128, с.194]. И, как точно отмечает далее Н.Ф. Талызина, получение определения понятия — это лишь первый шаг на пути усвоения понятия. Следующий шаг — включение определения понятия в действия учащихся с соответствующими объектами (выведение следствий определения, подведение под понятие, классификация понятия), которые они выполняют и с помощью которых в сознании учащихся создается понятие об этих объектах. Таким образом, овладение понятием предполагает: · усвоение определения понятия, которое является результатом действия определения (описания) понятия; · распознавание объектов, входящих в объем изученного понятия; · изучение существенных признаков понятия, не входящих в определение (выведение следствий из определения и изучение других свойств, представленных в теоремах); · выделение частных видов понятия или его обобщение; применение содержания понятия в решении задач и дальнейшем изучении предмета. Опишем структуру и содержание деятельности учащихся, систематическое и планомерное осуществление которой способствует формированию учебных действий, воспитанию познавательных привычек при изучении нового понятия. 4.2.1. Структура деятельности «введение понятия» Должен быть почитаем, как бог, тот,
|



 А О В
Рис. 18
А О В
Рис. 18
 Развернутым угломназывают угол, у которого стороны являются дополнительными полупрямыми (лучами).
Развернутый угол
Развернутым угломназывают угол, у которого стороны являются дополнительными полупрямыми (лучами).
Развернутый угол 
 :
: 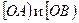 – дополнительные полупрямые (лучи).
– дополнительные полупрямые (лучи).

 :
:

 – дополнительные лучи.
– дополнительные лучи.

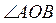 и
и 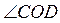 —
вертикальные углы.
Доказать:
—
вертикальные углы.
Доказать: 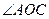 ,
, 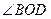 – развернутые
– развернутые
 ,
,