Деятельностный подход при обучении решению задач методом уравнений

Процесс решения задачи — деятельность, мотивом которой является потребность понимания того, как найти ответ на вопрос задачи, в частности, как уравнение помогает в этом. Заметим, что этот мотив может и не осознаваться школьниками. Но сегодня актуально в связи с формированием при обучении метода математического моделирования, чтобы этот мотив был осознанным. Целью процесса решения задачи, как описано выше для сюжетных задач, является необходимость выполнить требование, обозначенное в тексте. Действия «поиск плана решения задачи», «осуществление решения и его проверка» несколько изменяются. Поэтому вопросу обучения решению задач с помощью уравнений с точки зрения деятельностного подхода следует уделить особое внимание.

Понятно, что обучение применению уравнений к решению задач должно быть мотивировано. Мотивация осуществляется с осознания учеником собственного незнания, с понимания того, что он не может решать предложенную задачу известным методом. И в начальной школе, и в пропедевтическом курсе математики учащиеся должны овладеть арифметическим способом решения сюжетных (текстовых) задач [88, 107 и др.], что означает сформированность у них в том числе и действия поиска плана решения задачи (см. с. 105 – 110). Поэтому создание мотивационной ситуации с помощью задачи, которая вызывает у ученика непреодолимое затруднение, не столь важно. Проблемная ситуация в данном случае должна показать не просто незнание некоторого факта или метода [см., например, с. 19, 76 и др.], а способствовать осознанию того, что прежний способ рассуждения (правильный, испытанный временем, позволяющий успешно решать задачи) в данном случае не срабатывает. Познавательное затруднение учащихся следует сконцентрировать именно на методе рассуждения, известном им. Средством для такой мотивации деятельности служит способ поиска плана решения арифметической задачи по схеме восходящего анализа.

Проиллюстрируем это, используя задачу и поиск ее решения, рассмотренные выше (с. 109, рис. 34). Схема поиска приводит к арифметическому способу решения задачи. В результате анализа учащиеся формулируют план решения задачи, по которому можно составить числовое выражение: ((12+4)·3 + 8):(12 –4). Действие поиска плана решения задачи, ранее сформированное у младших школьников, является основой мотивации деятельности по изучению алгебраического метода решения задач. Чтобы произошло целеполагание (принятие учащимися цели деятельности), можно рекомендовать решить задачу, которая сыграет роль учебной задачи [33]. Цель изучения метода уравнений может быть поставлена самими учащимися после составления модели поиска решения специально подобранной задачи. Приведем пример задачи для 7-го класса.

Лодка шла по течению реки 3 часа и против течения 5 часов. Путь, пройденный лодкой по течению, оказался на 7 км длиннее пути, пройденного против течения. Найти скорость лодки в стоячей воде, если скорость течения реки 4 .

Составление модели поиска плана решения задачи не затрудняет учащихся, это для них известное действие. В результате получается, например, следующая модель рассуждения (рис. 38). Составленная схема обсуждается на уроке. Учащиеся приходят к выводу, что эта задача не сводится к известным величинам из условия задачи. Оказалось, что для ответа на вопрос задачи нужно знать этот ответ. Возник порочный круг. Известный прием поиска не дал результата: план решения задачи не найден. Нужен новый способ решения задачи.

Этот момент очень важен в мотивации учения. Возникает осознание учащимися «незнания» – известный способ рассуждения для решения задачи не дает результата. Построение модели поиска, полученной в результате организации учащихся для проведения анализа, приводит их к мысли о том, что следует считать искомое известным – обозначить через х. Тогда результат поиска

Скорость лодки в стоячей воде

?

Скорость лодки по течению

?

Скорость течения реки

4

Путь, пройденный лодкой по течению

? км

Время движения лодки по течению

3 ч

Путь, пройденный лодкой против течения

? км

Разность расстояний, пройденных по течению и против течения

7 км

Скорость лодки про­тив течения

?

Время движения лодки против течения

5 ч

Скорость лодки в стоячей воде

?

Скорость течения реки

4

 

Рис. 38

плана решения приведет к равенству с переменной – к уравнению!

Если учащиеся сами не приходят к этому выводу, учитель может подвести их к идее введения переменной, высказав после некоторой паузы свою «догадку»: «А что, если скорость лодки в стоячей воде считать известной? Пусть скорость лодки в стоячей воде х ».

Обычно в качестве неизвестной берут ту величину, о которой идет речь в главном вопросе (требовании) задачи. На первых этапах обучения решению задач методом уравнений этой рекомендации следует придерживаться, так как это, во-первых, проще психологически, во-вторых, после проверки сразу можно дать ответ [110]. Первоначально произвольность выбора переменной обсуждать нецелесообразно.

Таким образом, учащиеся подходят к новому способу решения задачи, к выбору неизвестного и обозначению его переменной: х — скорость лодки в стоячей воде. Отсюда с необходимостью следует (по схеме поиска см. рис. 37):

скорость лодки против течения: (х – 4) . Аналогично: путь, пройденный лодкой против течения ((х – 4)·5) км. Путь, пройденный лодкой по течению ((х– 4)·5+7) км; скорость лодки по течению (((х – 4)·5+7):3) ; скорость лодки в стоячей воде ((((х – 4)·5+7):3) – 4) , что равно х . Тогда получится уравнение: (((х – 4)·5+7):3) – 4 = х.

Сложность полученного уравнения[20] ориентирует на иной путь поиска плана решения задачи. После выполнения первого действия ПРЗ (изучения задачи), осознания необходимости использования метода уравнений, главный вопрос поиска плана решения задачи— значения каких величин равны по условию задачи? Или — установите, какие выражения (значения величин) целесообразно приравнять для составления уравнения [110], позднее можно говорить о составлении схемы уравнения [61]. Обозначив за х — скорость лодки в стоячей воде, можно последовательно найти:

· скорость лодки по течению (х + 4) ;

· путь, пройденный по течению ((х + 4) ·3) км;

· скорость лодки против течения (х – 4) ;

· путь, пройденный лодкой против течения ((х – 4)·5) км;

· путь лодки по течению ((х – 4)·5 + 7) км.

Путь, пройденный лодкой по течению реки, равен ((х – 4) ·5+7) км, с одной стороны, а с другой стороны – (х +4)·3 км. Значения выражений (х – 4)·5+7 и (х + 4)·3 равны, можно составить уравнение: (х – 4)·5+7 = (х + 4)·3. Полезно составление учащимися разных уравнений, например:

х +4 = ((х – 4)·5 + 7):3; (х +4)·3 – (х – 4)·5 = 7 и т.п.,

и обсуждение полученных результатов.

Таким образом, план решения задачи, решаемой с помощью уравнения, следующий:

1) выбор неизвестной величины и обозначение ее переменной (буквой);

2) перевод условия задачи на математический язык;

3) составление уравнения (модели) и его решение.

Действие осуществления плана решения задачи завершается решением уравнения (неравенства, системы уравнений или неравенств).

Для решения задачи предпочтение отдается уравнению наиболее простой структуры. Поиск решения задачи, осуществляемый, как видно из рассуждения, методом нисходящего анализа, не заканчивается нахождением корня уравнения. Как известно, метод нисходящего анализа завершается синтезом, который в решении задачи с помощью уравнения служит проверкой соответствия найденного корня уравнения условию задачи. Приведем ее.

Если 12,5 — скорость лодки в стоячей воде, то скорость лодки по течению 16,5 ; путь, пройденный лодкой по течению, (16,5·3 = 49,5) км; скорость лодки против течения 8,5 ; путь, пройденный лодкой против течения, (8,5·5 = 42,5) км. Действительно, путь, пройденный лодкой по течению, на 7 км длиннее пути, пройденного против течения.

Исследование предмета деятельности — процесса решения задачи с помощью уравнения — явно показывает, что проверка найденного ответа (корня уравнения) по условию является составной частью решения задачи. Таким образом, формирование действия контроля объективно присуще этой деятельности. Поэтому должен восприниматься странным вопрос учащегося к учителю: «Какой ответ в задаче?». Реакция учителя на него должна быть однозначной: «Закончите решение задачи» (что означает – сделайте проверку). И нельзя на проверке экономить время урока, наоборот, следует использовать в полной мере ПРЗ для воспитания школьников: формирования познавательной привычки к контролю своей деятельности.

Таким образом, процесс решения задач с помощью уравнений (неравенств, систем уравнений и неравенств) как деятельность обладает большим потенциалом для формирования метода математического моделирования, с одной стороны, и способствуют становлению общеучебной компетентности школьников [21], с другой. Постепенно становится реальностью личностно ориентированная парадигма образования, основанная на компетентностном подходе [88]. Формирование компетентностей требует создания определенных условий организации процесса обучения, которые могут быть реализованы с помощью деятельности как процесса, который характеризуется «психологически следующим: то, на что направлен данный процесс в целом (его предмет), всегда совпадает с тем объективным, что побуждает субъекта к данной деятельности, то есть мотивом» [63, с. 518].

Компетентность в процессе решения задачи означает:

1) понимание фабулы задачи, смысла отдельных слов и выражений, структуры задачи; умение устанавливать зависимости между известными и неизвестными величинами, выделять главный вопрос задачи; привычку выполнения краткой записи задачи (построения модели);

2) знание сути методов восходящего и нисходящего анализа, умение и привычку в их применении для поиска плана решения задачи, опыт в осуществлении действия поиска решения задачи;

3) умение осуществлять выработанный план решения задачи, опыт выполнения этого действия;

4) умение и привычку проверять полученные результаты, соотносить их с реальными жизненными ситуациями; опыт выполнения действия изучения полученных результатов.
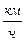