ЗАКЛЮЧЕНИЕ. Изложение основных положений психологической теории деятельности, общей структуры деятельности выполнено с использованием иллюстративных примеров из
Изложение основных положений психологической теории деятельности, общей структуры деятельности выполнено с использованием иллюстративных примеров из теоретического курса методики преподавания математики и осуществляемой автором практики обучения математике учащихся средней школы, а также методике обучения математике студентов. При этом принцип единства деятельности внутренней (психической) и внешней (материализованной внутренней) реализован в описании компонентов деятельности. Понимание и принятие автором положения о том, что принцип предметности составляет ядро психологической теории деятельности, в данной работе представлено результатами исследования категориального аппарата по понятию как форме мышления и теореме как виде суждения. Эти результаты использованы в разработке таких видов деятельности учащихся при обучении математике, как «введение понятия» и «изучение утверждения». В монографии показано, что в теории и методике, технологиях обучения математике вопросы обучения понятиям и суждениям до сих пор представлены традиционно, без глубокого анализа их с позиций деятельности. Применяя деятельностный подход к процессу обучения математике в школе, нами выделены виды деятельности, которые следует формировать у учащихся средней школы. О том, что знания формируются в деятельности и иначе как в деятельности полноценно усвоены быть не могут, говорят в своих трудах психологи Н.Ф. Талызина, В.В. Давыдов, Л.М. Фридман, дидакты Г.И. Щукина, П.И. Пидкасистый и их последователи. Автором предприняты значительные усилия по претворению основных положений деятельностного подхода, обозначенного в трудах Н.Ф. Талызиной и П.И. Пидкасистого, в технологии обучения математике учащихся средней школы. Исследование каждого из выделенных видов деятельности учащихся при обучении математике с точки зрения общей структуры деятельности позволило нам представить их структурные элементы: мотивацию, целеполагание, действия и операции, из которых складывается каждый вид деятельности. Описание целей, порождаемых мотивом, и соответствующих им действий, операций может быть использовано в практической работе учителя математики и при подготовке будущих учителей математики. Формирование познавательного инструментария учащихся в ходе деятельности есть воспитание соответствующих познавательных привычек, по терминологии Е.А. Дышинского (из неопубликованных работ). Список литературы 1. Абульханова-Славская, К. А. Деятельность и психология личности / К. А. Абульханова-Славская. – М.: Наука, 1980. – 335 с. 2. Алгебра и начала анализа: учеб. для 10—11 кл. сред. шк. / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; под редакцией А. Н. Колмогорова. — М.: Просвещение, 1990. — 320 с. 3. Алгебра: учеб. для 7 кл. общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. В.Суворова; под ред. С. А. Теляковского. – М.: Просвещение, 1997. – 240 с. 4. Алгебра: учебник для 8 кл. ср. шк. / Ю. Н. Макарычев, 5. Алгебра: учебник для 9 кл. ср. шк. / Ю. Н. Макарычев, 6. Антипов, И. Н. Символы, обозначения, понятия школьного курса математики: пособие для учителей / И. Н. Антипов, Л. С. Шварцбурд. – М.: Просвещение, 1978. – 64 с. 7. Асмолов, А. Г. Психология личности / А. Г. Асмолов. – М.: Смысл: Академия, 2002. – 112 с. 8. Балл, Г. А. Теория учебных задач: психолого-педагогический аспект / Г. А. Балл. – М.: Педагогика, 1990. – 183 с. 9. Богоявленский, Д.Н. Психология усвоения знаний в школе / Д. Н. Богоявленский, Н.А. Менчинская. – М.: Изд-во АПН РСФСР, 1959. – 348 с. 10. Беспалько, В. П. Слагаемые педагогической технологии / В. П. Беспалько. – М.: Педагогика, 1989. – 190 с. 11. Болтянский, В. Г. Как устроена теорема? / В. Г. Болтянский // Математика в школе. – 1973. – № 1. – С.41– 49. 12. Васильева, Г. Н. О видах деятельности учащихся на уроках математики / Г. Н. Васильева // Реализация деятельностного подхода при обучении математике в средней школе: сб. ст. / под ред. Г. Н. Васильевой. – Пермь, 2003. – С. 4–13. 13. Васильева, Г. Н. О деятельностном подходе при введении понятий // Педагогические идеи Е.А. Дышинского и современное математическое образование: материалы науч.-практ. конференции преподавателей математики вузов и сузов, посвященной 80-летию со дня рождения Е.А. Дышинского / гл. ред. Г. Н. Васильева; Перм. гос. пед. ун-т. – Пермь, 2005. – С. 130 – 135. 14. Васильева, Г. Н. О содержании основного общего математического образования / Г.Н. Васильева // Методики и технологии математического образования: сборник трудов по материалам II международной научной конференции «Математика. Образование. Культура». Ч. 3. — Тольятти: ТГУ, 2005.—С.17–22. 15. Васильева, Г.Н. Реализация деятельностного метода обучения на примере изучения логарифмов в средней школе // Проблемы реализации творческого потенциала личности в процессе обучения математике: межвузовский сборник научно-методических трудов. – Екатеринбург: УрГПУ, 2001. 16. Васильева, Г.Н. Об изложении курса алгебры основной школы с позиций деятельностного подхода в обучении // Актуальные проблемы преподавания математики в педагогических вузах и средней школе: тез. докл. XXIII Всерос. семинара преподавателей математики ун-тов и пед. вузов, 13—15 октября 2004 г./ гл. ред. Е.В. Яковлев. — Челябинск. 2004. — С. 197. 17. Ведерникова, Т.Н. Интеллектуальное развитие школьников на уроках математики / Т.Н. Ведерникова, О.А. Иванов // Математика в школе. — 2002. — № 3. — С. 41. 18. Виленкин, Н. Я. Алгебра для 8 класса: учебное пособие для учащихся школ и классов с углубленным изучением математики. – М.: Просвещение, 1995. – 256 с. 19. Виленкин, Н. Я. Современные основы школьного курса математики / Н. Я. Виленкин. – М.: Просвещение, 1980. – 377 с. 20. Виноградова, Л. В. Методика преподавания математики в средней школе: учеб. пособие / Л. В. Виноградова. – Ростов н/Д: Феникс, 2005. – 252 с. 21. Виноградова, Н. Ф. Индивидуализация обучения в начальной и профильной школах: парадоксы взаимодействия / Н. Ф. Виноградова // Профильная школа. – 2003. – №2. 22. Волович, М. Б. Ключ к пониманию алгебры. Пособие для учителя, ученика и его родителей / М. Б. Волович. – М.: Аквариум, 1997. – 272 с. 23. Волович, М. Б. Наука обучать. Технология преподавания математики / М. Б. Волович. – М.: LINKA – PRESS, 1995. – 280 с. 24. Володин, В. К. Несколько задач на движение плоскости / В.К. Володин, С.В. Фролова // Математика в школе. — 2000. — № 4. — С. 8. 25. Вопросы общей методики преподавания математики: учеб. пособие для студентов-заочников III-IV курсов физ.- мат. фак. пед. ин-тов. – М.: Просвещение, 1979. – 80 c. 26. Выготский, Л. С. Избранные психологические исследования/ Л. С. Выготский. – М.: АПН РСФСР, 1956. – 520 с. 27. Выготский, Л. С. Умственное развитие детей в процессе обучения / Л. С. Выготский. – М.: Учпедгиз, 1935. – 135 с. 28. Гальперин, П. Я. О психологических основах программированного обучения / П. Я. Гальперин // Новые исследования в педагогических науках: сб. ст. – М., 1965. – Вып. 4. – С. 21–26. 29. Ганеев, Х. Ж. Теоретические основы развивающего обучения математике / Х. Ж. Ганеев. — Екатеринбург, 1997. — 160 с. 30. Гастева, С. А. Методика преподавания математики в восьмилетней школе. / С. А. Гастева, Б. И. Крельштейн, С. Е. Ляпин, М. И. Шидловская; под общей ред. С. Е. Ляпина. – М.: Просвещение, 1965. — 743 с. 31. Давыдов, В. В. Проблемы развивающего обучения: опыт теоретического и экспериментального психологического исследования/ В. В. Давыдов — М.: Изд-во «Академия», 1986. – 240 с. 32. Давыдов, В. В. Состояние и проблемы исследования учебной деятельности / В. В. Давыдов // Деятельностный подход в психологии: проблемы и перспективы: сб. науч. тр. / под ред. В. В. Давыдова, Д. А. Леонтьева. – М., 1990. – С. 3–18. 33. Давыдов, В.В. Содержание и структура учебной деятельности учащихся/ В.В. Давыдов // Формирование учебной деятельности школьников. — М., 1982. — С. 10–21. 34. Дегтянникова, И.Н. Построение моделей к задачам с полными и неполными данными / И.Н. Дегтянникова // Математика в школе. — 2001. — № 2. — С. 15. 35. Деятельность: теория, методология, проблемы. – М.: Политиздат, 1990. – 366 с. 36. Дидактика средней школы: некоторые проблемы современ. дидактики / под ред. М. Н. Скаткина. – М.: Просвещение, 1982. – 319 с. 37. Дорофеев, Г. В. Математика. 5 класс: в 3-х частях / Г. В. Дорофеев, Л. Г. Петерсон. – М.: Ювента: Просвещение, 1996. 38. Дорофеев, Г. В. Математика. 6 класс: в 3-х частях / Г. В. Дорофеев, Л. Г. Петерсон. – М.: Баласс: С-инфо, 1998–1999–2002. 39. Дусавицкий, А.К. Развитие личности в учебной деятельности / А. К. Дусавицкий. — М.: Дом педагогики, 1996. — 208 с. 40. Епишева О.Б. Общая методика обучения математике в средней школе: курс лекций: учеб. пособие для студентов физ.-мат. спец. пед. ин-тов / О.Б. Епишева – изд. 2-е, доп. и перераб. – Тобольск: Изд-во ТГПИ им. Д.И. Менделеева, 2008.– 203 с. 41. Епишева, О. Б. Технология обучения математике на основе деятельностного подхода: кн. для учителя / О. Б. Епишева. – М.: Просвещение, 2003. – 223 с. 42. Епишева, О. Б. Учить школьников учиться математике: формирование приемов учеб. деятельности: кн. для учителя / О. Б. Епишева, В. И. Крупич. – М.: Просвещение, 1990. – 128 с. 43. Загвязинский, В. И. Теория обучения: современная интерпретация: учеб. пособие для студентов высш. пед. учеб. заведений / В. И. Загвязинский. – М.: Академия, 2001. – 192 с. 44. Зильберберг, Н. И. Приобщение к математическому творчеству. / Н. И. Зильберберг. – Уфа: Башкирское книжное издательство, 1988. – 96 с. 45. Зимняя, И. А. Ключевые компетенции – новая парадигма результата образования / И. А. Зимняя // Высшее образование сегодня. – 2003. – № 5. – С. 34–42. 46. Знакомимся с алгеброй: учеб. пособие по математике для 7 кл. / Э. Г. Гельфман, С. Я. Гриншпон, Л. Н. Демидова и др.; Том. ун-т. – Томск, 1994. – 248 с. 47. Иванова, Т. А. Гуманитаризация общего математического образования: моногр. / Т. А. Иванова; Н. Новгород. гос. пед. ун-т. – Н. Новгород, 1998. – 206 с. 48. Кабанова-Меллер, Е. Н. Учебная деятельность и развивающее обучение / Е. Н. Кабанова-Меллер. – М.: Знание, 1981. – 96 с. 49. Каменская, Е. И. Основы психологии: конспект лекций / Е. И. Каменская. – Ростов н/Д: Феникс, 2005. – 192 с. 50. Канин, Е.С. Заключительный этап решения учебных задач / Е.С. Канин, Ф.Ф. Нагибин. // Преподавание алгебры и геометрии в школе. — М.,1982. — 223 с. 51. Клековкин, Г. А. Некоторые аспекты использования компьютера в свете деятельностного подхода к обучению / Г. А. Клековкин // Методики и технологии математического образования: сб. тр. по материалам ΙΙ Междунар. науч. конф. "Математика. Образование. Культура", г. Тольятти 1–3 нояб. 2005 г. – Тольятти: ТГУ, 2005. 52. Колягин, Ю.М. Задачи в обучении математике: в 2-х частях /Ю. М. Колягин. — М.: Просвещение. — 1977. 53. Концепция структуры и содержания общего среднего образования (в 12-летней школе): проект // Математика в школе.— 2000. № 2. — С. 6. 54. Концепция математического образования (в 12-летней школе): проект // Математика в школе.— 2000. № 2. — С. 13. 55. Крутецкий, В. А. Психология математических способностей школьников / В. А. Крутецкий. – М.: Просвещение, 1968. — 432 с. 56. Крупич, В. И. Теоретические основы обучения решению школьных математических задач / В.И. Крупич. — М., 1995. — 166 с. 57. Купавцев, А. В. Деятельностная альтернатива в образовании / А. В. Купавцев // Педагогика. – 2005. – № 10. – С. 27–33. 58. Лазарев, В. С. Критерии и уровни готовности будущего педагога к исследовательской деятельности / В. С. Лазарев, Н. И. Ставринова // Педагогика. –2006. – № 2. – С. 51–59. 59. Лебедева, И. П. Теория взаимодействия систем «ученик» и «объект изучения» / И. П. Лебедева; Перм. гос. пед. ун-т. – Пермь, 2001. – 200 с. 60. Лебедева, И. П. Математическое моделирование в педагогическом исследовании: моногр. / И. П. Лебедева; Перм. гос. пед. ун-т. – Пермь, 2003. – 122 с. 61. Левитас, Г.Г. Об алгебраическом решении текстовых задач // Математика в школе. — 2000. — № 8. — С. 13. 62. Леонтьев, А. Н. Деятельность. Сознание. Личность / А. Н. Леонтьев. – М.: Политиздат, 1975. – 304 с. 63. Леонтьев, А. Н. Проблемы развития психики/ А. Н. Леонтьев.— М., 1981. — 584 с. 64. Леонтьев, А. Н. Избранные психологические произведения: в 2 т. Т.2 / А. Н. Леонтьев. – М.: Педагогика, 1983. – 320 с. 65. Лернер, И. Я. Процесс обучения и его закономерности / И. Я. Лернер. – М.: Знание, 1980. – 96 с. 66. Лихачев, Б.Т. Воспитательные аспекты обучения: учеб. пособие по спецкурсу для студентов пед. ин-тов. —М.: Просвещение, 1982. — 192 с. 67. Лященко, Е. И. Методика обучения математике в 4-5–х классах / Е.И.Лященко, А.А. Мазаник — Минск: Нар. асвета, 1976. — 222 с. 68. Лященко, Е. И. Лабораторные и практические работы по методике преподавания математики: учеб. пособие для студентов физ.-мат. спец. пед. ин-тов / Е. И. Лященко, К. В. Зобкова, Т. Ф. Кириченко и др. – М.: Просвещение, 1988. – 223 с. 69. Маркова, А.К. Формирование учебной деятельности и 70. Маркова, А. К. Формирование мотивации учения: кн. для учителя/ А. К. Маркова, Т. А. Матис, А. Б. Орлов. – М.: Просвещение, 1990. – 230 с. 71. Математика: учеб. для 5 кл. ср. шк. / Н. Я. Виленкин, А. С. Чесноков, С. И. Шварцбурд, В. И. Жохов. – 3-е изд., испр. и доп. – М.: Мнемозина, 1995. – 384 с. 72. Матушкина, З.П. Приемы обучения учащихся решению математических задач: учебное пособие. — Курган: Изд-во Курганского гос. ун-та, 2003. – 256 с. 73. Махмутов, М. И. Проблемное обучение. Основные вопросы теории / М. И. Махмутов. – М.: Педагогика, 1975. – 368 с. 74. Мельникова, Е. Л. Проблемный урок или как открывать знания с учениками: пособие для учителя./ Е.Л. Мельникова. — М. — 2002. — 168 с. 75. Методика преподавания математики в средней школе. Общая методика: учеб. пособие для студентов физ.-мат. фак. пед. ин-тов/ В.А. Оганесян, Ю.М. Колягин, В.Я. Саннинский, Г.А. Луканкин. – М.: Просвещение, 1975. – 447 с. 76. Методика и технология обучения математике. Курс лекций: пособие для вузов / под научн. ред. Н. Л. Стефановой, Н. С. Подходовой. – М.: Дрофа, 2005. – 416 с. 77. Методика преподавания математики в средней школе: частная методика: учеб. пособие для студентов пед. ин-тов по физ.-мат. спец. / А. Я. Блох, В. А. Гусев, Г. В. Дорофеев и др.; сост. В. И. Мишин. – М.: Просвещение, 1987. – 416 с. 78. Миганова, Е.Ю. Обучение методам решения задач по теме «Треугольники» // Математика в школе. — 2002. — № 3. — С. 25. 79. Мордкович, А. Г. Алгебра. 7 кл.: в двух частях. Ч. 1: учеб. для общеобразоват. учреждений / А. Г. Мордкович. – 4-е изд., испр. – М.: Мнемозина, 2001. – 160 с. 80. Мордкович, А. Г. Алгебра 8 кл.: в двух частях. Ч. 1: учеб. для общеобразоват. учреждений / А. Г. Мордкович. — 4-е изд. – М.: Мнемозина, 2002.— 223 с. 81. Мордкович, А. Г. Алгебра 9 кл.: в двух частях. Ч. 1: учеб. для общеобразоват. учреждений / А. Г. Мордкович. — 4-е изд. – М.: Мнемозина, 2004.— 192 с. 82. Мордкович, А. Г. Алгебра и начала анализа. 10-11 кл.: учеб. для общеобразоват. учреждений / А. Г. Мордкович. – М.: Мнемозина, 2000.— 336 с. 83. Нешков, К. И. Функции задач в обучении // Математика в школе. — 1971. — №3. — С. 4. 84. Никитин, В. В. Определения математических понятий: пособие для учителей / В. В. Никитин, К. А. Рупасов. – М.: Учпедгиз, 1963. – 206 с. 85. Никифоров, А. Л. Деятельность, поведение, творчество / А. Л. Никифоров // Деятельность: теории, методология, проблемы. – М., 1990. – С. 52–69. 86. Никольская, И. Л. Учимся рассуждать и доказывать: кн. для учащихся 6–10 кл. сред. шк. / И. Л. Никольская, Е. Е. Семенов. – М.: Просвещение, 1989. – 192 с. 87. Новейший философский словарь / сост. А. А. Грицанов. – Минск, 1999. – 878 с. 88. Образовательный стандарт основной школы: материалы семинара, п. Салтыковка Моск. обл., 3–5 апреля 2002 г. – М., 2002. 89. Огурцов, А. П. Деятельность / А. П. Огурцов, Э. Г. Юдин // БСЭ: в 30 т. Т. 8. – 3-е изд. – М., 1972. – С. 180–181. 90. Ожегов, С.И. Словарь русского языка: 70 000 слов/ под ред. Н.Ю. Шведовой. —23-е изд., испр. — М.: Рус. яз., 1990. — 917 с. 91. Пайсон, Б. Д. О логической составляющей образовательной области "математика" / Б. Д. Пайсон // Математика в школе. – 2003. – № 2. – С. 10. 92. Педагогика: педагогические теории, системы, технологии: учебн. для студентов высш. и сред. пед. учеб. заведений / С. А. Смирнов, И. Б. Котова, Е. Н. Шиянов. – М.: Академия, 2004. – 509 с. 93. Педагогическая энциклопедия: в 4 т. Т. 4. – М., 1968. – С. 410–414. 94. Перельман, Я. И. Занимательная алгебра / Я. И. Перельман. – М.: Триада – литера, 1994. – 200 с. 95. Перминова, Л. М. Логико-дидактический подход к обучению / Л. М. Перминова // Педагогика. – 2004. – № 1. – С. 18–26. 96. Пехлецкий, И.Д. Компоненты индивидуального стиля преподавания: спецкурс–практикум. — Пермь: ПГПИ, 1990. — 138 с. 97. Пидкасистый, П. И. Искусство преподавания: первая кн. учителя / П. И. Пидкасистый, М. Л. Портнов. – М., 1999. – 212 с. 98. Пидкасистый, П. И. Самостоятельная познавательная деятельность школьников: теорет.-эксперим. исслед. / П. И. Пидкасистый. – М.: Педагогика, 1980. – 240 с. 99. Пичурин, Л. Ф. За страницами учебника алгебры: кн. для учащихся 7–9 кл. сред. шк. / Л. Ф. Пичурин. – М.: Просвещение, 1990. – 224 с. 100. Планы и методические рекомендации к практическим и 101. Погорелов, А.В. Геометрия: учебник для 7-9 классов общеобразовательных учреждений. — 5-е изд.— М.: Просвещение, 2004. — 224 с. 102. Пойа, Д. Как решать задачу. — М.: Квантор,. — 1991. — 216 с.. 103. Половникова, Н. А. О теоретических основах воспитания познавательной самостоятельности школьника в обучении / Н. А. Половникова // Ученые записки МП РСФСР / Казан. гос. пед. ин-т. – Вып. 47. – Казань, 1968. – 204 с. 104. Программа обучения математике в гимназии/ сост. Г.Н. Васильева, И.Д. Пехлецкий.— Пермь: ГКОН. — 1996. — 45 с. 105. Равен, Дж. Компетентность в современном обществе: выявление, развитие и реализация: пер. с англ. / Дж. Равен. – М.: Когито-центр. — 2002. – 394 с. 106. Развитие познавательной самостоятельности учащихся в процессе решения геометрических задач: (в обучении геометрии в шестом классе): автореф. дис. … канд. пед. наук / Г. Н. Васильева. – М., 1982. – 16 с. 107. Региональный стандарт для общеобразовательных учреждений Пермской области: "Математика" /Департамент образования и науки администрации Перм. области; ПГПУ. – Пермь, 2001. 108. Репкин, В. В. Развивающее обучение: теория и практика / В.В. Репкин, Н. В. Репкина. – Томск: Пеленг, 1997. – 288 с. 109. Репкин, В. В. Развивающее обучение и учебная деятельность / В.В. Репкин. — Рига, 1992. — 44 с. 110. Репьев, В.В. Методика преподавания алгебры в 8-летней школе: учеб. пособие для студентов мат. спец. пед. вузов. — М.: Просвещение, 1967.— 223 с. 111. Рогов, А. Т. Важнейшее требование теории учебника / А. Т. Рогов // Проблемы школьного учебника: сб. ст. – М., 1974. – С. 101–113. 112. Рубинштейн, С. Л. Основы общей психологии / С. Л. Рубинштейн. – СПб.: Питер Ком, 1998. – 705 с. 113. Саранцев, Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / Г. И. Саранцев. – М.: Просвещение, 2002. – 223 с. 114. Саранцев, Г. И. Обучение математическим доказательствам в школе / Г. И. Саранцев. – М.: Просвещение, 2000. – 171 с. 115. Саранцев, Г. И. Формирование математических понятий в средней школе / Г. И. Саранцев // Математика в школе. – 2003. – № 10. – С. 6–10. 116. Селевко, Г. К. Современные образовательные технологии: учеб. пособие / Г. К. Селевко. – М.: Народное образование, 1998. – 256 с. 117. Селиверстова, Е. Н. Развивающая функция обучения: современный дидактический взгляд / Е. Н. Селиверстова // Педагогика. – 2006.– № 4. – С. 45–52. 118. Семиряжко, В. А. Философский и методический аспекты разработки современных учебников по математике / В. А. Семиряжко // Математика в школе. – 2006. – №9.– С. 50–54. 119. Сериков, В. В. Личностно-ориентированное образование / В. В. Сериков // Педагогика. – 1994. – № 5. – С. 17–18. 120. Сериков, В. В. Личностный подход в образовании: концепция и технологии: моногр. / В. В. Сериков. – Волгоград: Перемена, 1994. – 150 с. 121. Слепкань, З.И. Психолого-педагогические основы обучения математике / З. И. Слепкань. – Киев: Рад. Школа, 1983. – 192 с. 122. Смирнов, С. Д. Педагогика и психология высшего образования. От деятельности к личности: учеб. пособие для студентов высш. учеб. заведений / С. Д. Смирнов. – М.: Академия, 2005. – 393 с. 123. Современные аспекты методики обучения математике: учеб. пособие / Т.Л. Блинова, Э.А. Власова, И.Н. Семенова, А.В. Слепухин; под. ред. И.Н. Семеновой, А.В. Слепухина; ГОУ ВПО «Урал. гос. пед. ун-т». — Екатеринбург. 2007. —190 с. 124. Степень и ее свойства: методическая разработка. / Перм. гос. пед. ун-т; авторы-сост. Г.Н. Васильева, И.Н. Власова — Пермь, 2001. – 20 с. 125. Столяр, А. А. Логическое введение в математику / А. А. Столяр. – Минск: Вышэйш. шк., 1971. – 222 с. 126. Столяр, А. А. Педагогика математики: курс лекций / А. А. Столяр. – 2-е изд., перераб. и допол. – Минск: Вышэйш. шк., 1986. – 414 с. 127. Талызина, Н.Ф. Что значит знать? / Н. Ф. Талызина // Советская педагогика. – 1980. – № 8. — С. 97. 128. Талызина, Н. Ф. Педагогическая психология: учеб. для студентов учеб. заведений сред. проф. образования / Н. Ф. Талызина. – М.: Академия, 2003. – 288 с. 129. Тарасенкова Н.А. Пропедевтический этап обучения поиску дополнительных построений./ Н.А. Тарасенкова // Математика в школе. — 2000. — № 4. — С. 32. 130. Теоретические основы обучения математике в средней школе: учебное пособие / Т. А. Иванова, Е.Н. Перевощикова, Т.П. Григорьева, Л.И. Кузнецова; под ред. Проф. Т.А Ивановой. — Н. Новгород: НГПУ, 2003. – 320 с. 131. Технологии и методики обучения: методические рекомендации. Часть 1 / сост. Г.Н. Васильева, И.В. Косолапова. — Пермь, 2002. — 43 с. 132. Тимофеева Н.М. Словник к методическому словарю по обучению математике / под ред. Г.Е Сенькиной – Смоленск: СГПУ, 2003. – 40 с. 133. Третьяков П.И. Технология модульного обучения в школе: практико-ориентированная монография / под ред. П.И. Третьякова. – М.: Новая школа, 1997. — 352 с. 134. Усова, А. В. Психолого-дидакические основы формирования у учащихся научных понятий: пособие по спецкурсу / А. В. Усова; Челябинский пед. ин-т. – Челябинск, 1988. – 89 с. 135. Фридман, Л.М. Теоретические основы методики обучения математике/ Л.М. Фридман. — М.: Издательство «Флинта», 1998. — 224 с. 136. Фридман, Л. М. Логико-психологический анализ школьных учебных задач / Л. М. Фридман. – М.: Просвещение, 1977. – 208 с. 137. Фридман, Л. М. Как научиться решать задачи: беседы о решении мат. задач. Пособие для учащихся/ Л.М. Фридман, Е.Н. Турецкий, В.Я. Стеценко; под ред. Л.М. Фридмана. — М.: Просвещение, 1979. — 160 с. 138. Фридман, Л.М. Психолого-педагогические основы обучения математике в средней школе/ Л.М. Фридман. — М.: Просвещение, 1983. 139. Хуторской, А. В. Деятельность как содержание образования / А. В. Хуторской // Народное образование. – 2003. – № 8. – С. 107–114. 140. Хуторской, А. В. Ключевые компетенции как компонент личностно-ориентированной парадигмы образования / А. В. Хуторской // Нар. образование. – 2003. – № 2. – С. 58–64. 141. Хуторской, А. В. Дидактическая эвристика. Теория и технология креативного обучения / А. В. Хуторской. – М.: МГУ, 2003. – 416 с. 142. Хуторской, А. В. Практикум по дидактике и современным методикам обучения: учеб. пособие / А. В. Хуторской. – 3-е изд., дораб. – СПб.: Питер, 2004. – 541с. 143. Хуторской, А. В. Место учебника в дидактической системе / А. В. Хуторской // Педагогика. – 2005. – № 4. – С. 10–18. 144. Швырев, В. С. Проблемы разработки понятия деятельности как философской категории / В. С. Швырев // Деятельность: теории, методология, проблемы. – М., 1990. – С. 9–20. 145. Шимина, А. Н. Логико-гносеологические основы процесса формирования понятий в обучении: пособие к спецкурсу для студентов пед. ин-тов / А. Н. Шимина. – М., 1981. – 75 с. 146. "Школа 2000…". Математика. 5–6 классы: метод. материалы к учеб. математики Г. В. Дорофеева, Л. Г. Петерсон / сост. Л. Г. Петерсон. – М.: УМЦ "Школа 2000…", 2003. – 240 с. 147. Щукина, Г. И. Активизация познавательной деятельности в учебном процессе: учеб. пособие для пед. ин-тов / Г. И. Щукина. – М.: Просвещение, 1979. – 160 с. 148. Щукина, Г. И. Роль деятельности в учебном процессе: кн. для учителя / Г. И. Щукина. – М.: Просвещение, 1986. – 142 с. 149. Эльконин, Д. Б. Психология обучения младшего школьника / Д.Б. Эльконин. – М.: Знание. — 1974.— 64 с. 150. Эльконин, Д. Б. Избранные психологические труды / Д. Б. Эльконин; под ред. В.В. Давыдова, В. П. Зинченко – М.: Педагогика, 1989. – 554 с. 151. Якиманская, И. С. Личностно ориентированное обучение в современной школе. — М.: Сентябрь. — 1996. — 96 с. 152. Ястребов, А. В. Задачи по общей методике преподавания математики: учебное пособие / А. В. Ястребов. — Ярославль: Изд-во ЯГПУ, 2009. — 148 с. [1] В учебнике геометрии, как правило, сформулирована сложная теорема. [2] Задачи аналогичные первым геометрическим задачам ученики решали в 5–6 классах при изучении геометрических фигур. Однако требование строгого обоснования их решения не являлось обязательным. [3] Слово «существенный» выделено автором монографии. Ниже будет показана избыточность данного определения, использующего указанный термин. [4] Понятие «признак» в данном изложении отличается от термина, используемого в школьном курсе математики в качестве названия некоторых теорем. [5] ПРИЗНАК, примета, знак, симптом, показатель [Словарь синонимов русского языка, 1975, с. 414]. [6] СВОЙСТВО, см. качество [Там же, с. 481]. КАЧЕСТВО, свойство, черта, особенность, штрих, принадлежность, атрибут [Там же, с. 192].
[7]Существенный – значит, необходимый [90] (см с. 50 данной работы). Термин «необходимый» использовать не будем в сочетании с термином «существенный», как это встречается в литературе, например, [20, с. 6]. [8] Мы понимаем субъективность нашего мнения по этому поводу. Однако проводим анализ введения понятия по данному пособию, поскольку методика введения практически не изменяется и в систематическом курсе алгебры [3]. [9] Математический энциклопедический словарь./Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С. Бахвалов, В.И. Битюцков и др. — М.: Сов. энциклопедия, 1988, с. 580. [10] Как известно, вместо словосочетания «необходимо и достаточно» могут быть использованы и другие: «если и только если», «тогда и только тогда» и т.п. [11] В учебной литературе имеются два подхода к определению понятия: арифметическим квадратным корнем их числа а называется неотрицательное число, квадрат которого равен а [4, с. 66]; квадратным корнем из неотрицательного числа а называют такое неотрицательное число, квадрат которого равен данному числу а [80, с. 88]. [12] Речь идет об определении понятия арифметического квадратного корня в первой трактовке [4]. Во втором случае [80] эти свойства понятия входят в определение: [13] Школьниками достаточно успешно усваивается, что «определением называют предложение, в котором разъясняется смысл новых слов» [38, ч.1, с.165]. [14] Структура определяющего понятия может быть конъюнктивной, дизъюнктивной или импликативной. [15] Организационная четкость — одно из требований к уроку математики [75, с. 308]. [16] Определение степени с натуральным показателем:
[17] Действие поиска доказательства теоремы — рассуждение, аналогичное поиску решения арифметической задачи. Школьники достаточно успешно усваивают, начиная с начальной школы (если этому целенаправленно обучать), как ставить себе вопросы и отвечать на них. Умение «решать задачу с конца» означает построение рассуждения: цепочки достаточных условий для ответа на главный вопрос задачи (см. ниже, с. 107). [18] Метод восходящего анализа, как известно, является методом доказательства [75, с. 52].
[19] С.Л. Рубинштейн учит, что мышление — это актуализация и применение знаний, которые являются единым процессом.
[20] О сложности уравнения для пятиклассников, а тем более для учащихся начальной школы, свидетельствует структура уравнения. Для его решения следует уверенно владеть решением уравнений путем нахождения компонента действия и свойствами арифметических действий. [21] Алгебра и начала анализа: Учебник для 10-11 кл. ср. шк. / Ш. А. Алимов, Ю. М. Колягин, Ю. С. Сидоров и др. – М.: Просвещение, 1994.
|


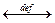
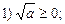
 .
. ,
, 
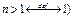
 2)
2)  (см. с.41).
(см. с.41).


