Локальная система задач как средство реализации деятельностного подхода в обучении математике
Совокупность задач, предназначенных для усвоения изучаемой темы, называют локальной системой задач. В методике преподавания математики сформулированы и обоснованы требования к системе как геометрических [106], так и других видов задач: 1) всестороннее отражение в системе задач признаков изучаемого понятия, свойств фигур во взаимосвязи с ранее изученными фактами посредством следующих задач: — взаимно-обратные; — задачи, имеющие различные способы решения; — задачи «без ограничений»; — «потенциально полезные». 2) сложность задач локальной системы различна; 3) наличие в системе задач, различающихся формой предъявления; 4) наличие задач с практической, занимательной (для младших школьников) фабулой, межпредметного содержания. Как правило, задачи в локальной системе задач расположены по их сложности, в соответствии с дидактическим принципом доступности. Под сложностью задачи понимается сложность структурной формулы решения, построенной на основе аналитико-синтетического поиска [106]. Требование наличия задач различной сложности позволяет не только осуществлять дифференцированный подход к обучению, но и развивать, например, умение проводить целенаправленный поиск плана решения задач методом восходящего или нисходящего анализа у учащихся, не владеющих ими. Деятельность ПРЗ очень подвижна (см. с. 13): она превращается в действие, например, при решении задачи с дидактической функцией: задач на распознавание или задач, ориентированных на формирование алгоритма. В задачах более сложной структуры (задачах с познавательной функцией) у многих учащихся действия превращаются в операции, если способ решения достаточно сформировался у школьника. Например, при решении аналогичных задач, при выполнении самостоятельной или контрольной работы. В процессе решения «потенциально полезных» и взаимно-обратных задач учащимися устанавливаются существенные связи между знаниями различных разделов курса алгебры, способствующие углублению и расширению их знаний. Процесс решения «потенциально полезных» задач и задач «без ограничений» способствует формированию умений учащихся вычленять, а затем формулировать новые задачи, ставить цели, намечать пути их достижения. Решение задач «без ограничений» развивает способность видеть частные, особые случаи, содействует формированию вариативности мышления. Важно отметить, что задачи «без ограничений» являются средством формирования метода полной индукции — одного из видов умозаключений, основанных «на рассмотрении в с е х единичных и частных суждений (случаев), относящихся к рассматриваемой ситуации» [75, с. 96]. Задачи, имеющие более одного способа решения, способствуют развитию эвристической деятельности учащихся. В поиске плана решения таких задач имеется возможность «открывать» способ решения, а не только ориентироваться на прием, используемый в аналогичных ситуациях. Вместе с тем все выделенные задачи показывают первостепенную роль качественно усвоенных знаний и, обратно, процесс решения задач способствует формированию изучаемых понятий. Приведем пример локальной системы задач к теме «Логарифм числа». Анализ локальной системы задач по теме «Логарифмы и их свойства» в учебниках алгебры [2] и др. позволяет сделать следующие выводы. Задачи в данной локальной системе расположены от простых к более сложным. Первые задачи системы направлены на усвоение определения логарифма. 1) Проверьте справедливость равенств: log 2) Используя равенства а) 3) Отметьте числа на координатной прямой: log Это задачи с дидактической функцией, процесс решения их — деятельность учащихся, функционирующая на основе изученного определения логарифма числа (в частности, логического действия подведения под понятие). Выполнение этих заданий способствует усвоению учащимися значений логарифмов чисел, часто встречающихся в решении уравнений и неравенств. Последующие задачи ориентированы на овладение свойствами логарифмов: · вычислите: lg 8 + lg 125; Среди задач данной локальной системы в одном из названных учебников имеются четыре взаимно-обратные [2]. Приведем пример: 1) прологарифмируйте по основанию 3 2) найдите x, если В других учебниках[21] такие задачи отсутствуют. Задачи, в которых новые понятия и их свойства используются в сочетании с изученными ранее, очень важны для развития самостоятельности учащихся. В анализируемых действующих учебниках таких заданий очень немного. Задачи, имеющие разные решения, «без ограничений» и «потенциально полезные» отсутствуют совсем. Поэтому данная локальная система требует дополнения. Среди задач конкурсных экзаменов, сборников для поступающих в вузы представлены задачи на тождественные преобразования логарифмических выражений. Приведем некоторые из них. 1. Сравните числа log 2. Вычислите: 36 3. Найдите log 4. Упростите: 5. Отметьте на координатной прямой числа: Последнее задание – проблема, которая ориентирует на изучение приближенных способов нахождения логарифмов: графический, табличный (В. М. Брадис), с помощью счетной линейки, калькулятора. В качестве «потенциально полезной» задачи можно предложить следующую: вычислите значение выражения: 3 После решения данной задачи учащиеся узнают новый факт, нужный в их дальнейшей математической деятельности: если а > 1 и х > 1 или 0 < a < 1 и 0 < x < 1, то справедливо равенство а В анализируемой локальной системе задач отсутствуют задачи межпредметного содержания. Данная система может быть дополнена следующей задачей: Докажите, что если a и b – длины катетов, а c – длина гипотенузы прямоугольного треугольника, то Сформулированные требования к локальной системе задач и их интерпретация, а также, например, приведенный выше анализ задач по теме «Арифметический квадратный корень» (см. с. 79 – 81) показывают, что проблема обеспечения формирования видов деятельности учащихся при обучении математике актуальна на современном этапе развития образования. Наш опыт реализации деятельностного подхода к обучению математике основан, в том числе, на использовании локальной системы задач, удовлетворяющих сформулированным требованиям. Организация деятельности учащихся по усвоению ими полноценных знаний — «знаний как убеждений» и развитию диалектического мышления — требует анализа каждой локальной системы задач и при необходимости ее дополнения недостающими заданиями. В первую очередь это касается упражнений, способствующих воспитанию познавательных привычек к проведению рассуждений методами восходящего и нисходящего анализа, полной индукции, к решению задачи разными способами.
|


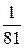 = – 4; log
= – 4; log  9 = – 2; log
9 = – 2; log 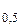 4 = – 2.
4 = – 2. найдите логарифмы чисел 9; 1; 25 по соответствующему основанию.
найдите логарифмы чисел 9; 1; 25 по соответствующему основанию.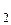 16; log
16; log 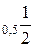 ; log
; log 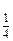
 .
.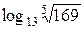 ;
;  .
. :
:  (№ 491 [2]);
(№ 491 [2]);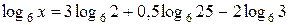 (№ 497 [Там же]).
(№ 497 [Там же]). 16 и 4.
16 и 4. + 10
+ 10  – 3
– 3  .
.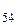 168, если log
168, если log  12 = a и log
12 = a и log  24 = b.
24 = b. [15];
[15];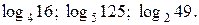
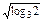 - 2
- 2  .
.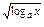 = х
= х  .
.