Практическая часть. Задача 1.Элементарный параллелепипед, находящийся в произвольном месте стальной конструкции подвергается действию системы напряжений
Задача 1. Элементарный параллелепипед, находящийся в произвольном месте стальной конструкции подвергается действию системы напряжений, лежащих в одной плоскости (рисунок 20).
Рисунок 20 - Элементарный параллелепипед Требуется найти: 1) главные напряжения и направление главных площадок; 2) максимальные касательные напряжения; 3) главные деформации 4) эквивалентное напряжение 5) относительное изменение объема; 6) удельную потенциальную энергию деформации. Исходные данные: Решение: При выполнении этой задачи необходимо руководствоваться следующим правилом знаков для нормальных и касательных напряжений: нормальное напряжение положительно, если оно направлено по внешней нормали к плоскости сечения, то есть оно является растягивающим, а сжимающее - отрицательно. Касательное напряжение по боковой грани призмы положительно, если изображающий его вектор до совмещения с внешней нормалью следует повернуть против часовой стрелки. Расставим знаки напряжений на рисунке 20. Получим: 1 Найдем главные напряжения
Главные напряжения обозначают
В задаче рассматривается плоское напряженное состояние, т.е. одно из трех главных напряжений равно нулю, поэтому из формулы (8) и правила (9) следует:
Направление главных площадок относительно заданных площадок, определяется по формуле:
Рисунок 21 – Распределение напряжений Отрицательный угол α0 откладывается по часовой стрелке от площадки с большим нормальным напряжением (в данном случае σх, на рисунке 21). Можно также пользоваться правилом: для определения положения главной площадки с напряжением σmax необходимо площадку с большим (в алгебраическом смысле) нормальным напряжением повернуть на угол α0 в направлении, в котором вектор касательного напряжения, действующего по этой же площадке, стремится вращать элементарный параллелепипед относительно его центра. 2 Найдем максимальные касательные напряжения. Они равны наибольшей полуразности главных напряжений:
3 Найдем главные деформации ε1, ε2 и ε3 из обобщенного закона Гука, приняв коэффициент Пуассона равным μ= 0,5:
4 Найдем эквивалентное напряжение σэкв
5 Найдем относительное изменение объема:
6 Найдем удельную потенциальную энергию деформации:
В данной задаче
Задача 2. Дано: a=5 см; b=2 cм; [σс]=100 МПа; [σр]=27 МПа. Определить напряжение, действующее в сечении (рис. 22). Решение: Найдем положение главных центральных осей, определив положение центра тяжести фигуры. Разобьем сложную фигуру на составляющие простые. Площадь фигуры
Откладываем эти координаты и проводим через центр тяжести точку С главные центральные оси z Найдем моменты инерции всей фигуры относительно осей
Изгибающие моменты входящие в формулу определения напряжения создаются силой F, которая приложена в точке А с координатами [-4,166;-4,166]
Наибольшее значение напряжений в растянутой и сжатой зонах можно вычислить если известны координаты опасных точек. Эти точки наиболее удалены то нейтральной оси, положение которых определяется отрезками
Квадраты радиусов инерции равны
Проведя нейтральную ось находим наиболее удаленные от нее точки С[-4.166;5.833]; В[5.833;-4.166]. Определим напряжение в этих точках
Рисунок 22- Эпюра напряжения, действующее в сечении В качестве допустимой нагрузки принимаем меньшее значение силы действующее при растяжении стержня
Задача 3. Для составного сечения, состоящего из швеллера №20 и уголка №14(10) (рисунок 23).
Рисунок 23- Составное сечение
Требуется: 1) определить положение центра тяжести; 2) найти величины осевых и центробежных моментов инерции относительно центральных осей; 3) определить направления главных центральных осей; 4) найти величины моментов инерции относительно главных нейтральных осей; 5) вычертить сечение в масштабе 1:2 и указать на нем все размеры в числах и все оси.
Вопросы для самопроверки 1 Что называется напряженным состоянием в данной точке деформируемого тела? 2 Какие имеются виды напряженного состояния материала? 3 Как определить напряжение на наклонной площадке растянутого стержня? 4 В чем заключается закон парности касательных напряжений? 5 Как называются площадки, по которым действуют наибольшие и наименьшие нормальные напряжения? 6 Какие напряжения называются главными? 7 Как производится графическое построение для определения напряжений в наклонных площадках в случае плоского напряженного состояния? 8 Чему равно наибольшее касательное напряжение в случае плоского и объемного напряженного состояния? 9 Напишите формулу обобщенного закона Гука. 10 Чему равно изменение объема при сложном напряженном состоянии? 11 Как определяется потенциальная энергия упругой деформации? 12 Как формируются основные теории прочности? 13 Как записывается условие прочности по этим теориям?
|


 1,
1,  по четвертой (энергетической) теории прочности;
по четвертой (энергетической) теории прочности; х = 90 МПа,
х = 90 МПа,  хy = 50 МПа.
хy = 50 МПа. = -90 МПа,
= -90 МПа,  = -80 MПa,
= -80 MПa,  = 50 МПа,
= 50 МПа,  =-50 МПа
=-50 МПа
 (8)
(8) при этом индексы расставляют так, чтобы выполнялось неравенство:
при этом индексы расставляют так, чтобы выполнялось неравенство: (9)
(9)


 МПа
МПа





 .
.




 .
. :
:



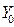








 Откуда
Откуда


 откуда
откуда





