Практическая часть. Задача 1.К стальному валу приложены скручивающие моменты: М1 , M2 , M3 , M4 (рисунок 24).
Задача 1. К стальному валу приложены скручивающие моменты: М 1, M 2, M 3, M 4 (рисунок 24).
Рисунок 24- Стальной вал
Требуется: 1) построить эпюру крутящих моментов; 2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшего большего значения из данного ряда диаметров 30, 35, 40,45, 50, 60, 70, 80, 90, 100 мм; 3) построить эпюру углов закручивания; 4) найти наибольший относительный угол закручивания. Исходные данные: М1 = М3 = 2 кНм, М2 = М4 = 1,6 кНм, а = b = с = 1,2 м, [τ] = 80 МПа,[μ]=0,3. Решение. 1 Построить эпюру крутящих моментов. Крутящие моменты, возникающие в поперечных сечениях брусьев, определяются с помощью метода сечений. Крутящие моменты в произвольных поперечных сечениях бруса численно равны алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения. Рассекая последовательно участки вала, получим:
По значениям этих моментов строим эпюру Мк в выбранном масштабе. Положительные значения Мк откладываем вверх, отрицательные - вниз от нулевой линии эпюры (рисунок 25). 2 При заданном значении [τ] определим диаметр вала из расчета на прочность. Условие прочности при кручении имеет вид:
где
Рисунок 25- Эпюры внутренних силовых факторов при кручении
Принимаем d = 50 мм = 0,05 м. 3 Построим эпюру углов закручивания вала. Угол закручивания участка вала длиной l постоянного поперечного сечения определяется по формуле
где GJ р - жесткость сечения вала при кручении. Модуль сдвига для стали
. Jp - полярный момент инерции круглого вала. Вычислим углы закручивания сечений В, С, D и К относительно закрепленного конца вала (сечения А) φА=0
Строим эпюру углов закручивания (рисунок 23). 4 Найдем наибольший относительный угол закручивания
Задача 2. Дано: L=0,86м; С1=0.22м; С2=0.48м; С3=0.62м; d1/d=4; d2/d=2; М1=2кНм; М2=-4кНм; М3=-6кНм;
Рисунок 26- Схема нагружения стержня Вопросы для самопроверки 1 Дайте определение понятия "крутящий момент в поперечном сечении бруса". 2 Что такое эпюра крутящих моментов? Как производить ее построение? 3 Какие напряжения возникают в поперечном сечении круглого стержня при кручении? Как находится их величина в произвольной точке поперечного сечения? 4 Как нужно нагрузить брус, чтобы он работал только на кручение? 5 Каким образом определить в любом поперечном сечении бруса величину крутящего момента? 6 Сформулируйте правило знаков при определении величины крутящего момента. 7 На каких гипотезах и допущениях основаны выводы расчетных зависимостей при кручении? 8 По какому закону распределяются напряжения в поперечном сечении круглого бруса при кручении? 9 Какой величиной характеризуется величина деформации при кручении? 10 По каким формулам определяются величины деформации кручения (относительный угол закручивания) в радианах на метр и в градусах на метр? 11 Что такое полярный момент инерции поперечного сечения бруса? 12 По каким формулам определяется полярный момент инерции круга и кругового кольца? 13 Что такое жесткость сечения бруса? 14 Как определяется при кручении напряжение в любой точке круглого поперечного сечения бруса и как определяется наибольшее напряжение?
|



 - абсолютная величина максимального крутящего момента на эпюре Мк (рисунок 25).
- абсолютная величина максимального крутящего момента на эпюре Мк (рисунок 25).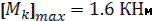 ;
; - полярный момент сопротивления для сплошного круглого вала. Диаметр вала определяется по формуле
- полярный момент сопротивления для сплошного круглого вала. Диаметр вала определяется по формуле








 ;
;  ; М=2кНм.
; М=2кНм.



