Теоретическая часть. При изучении явления продольного изгиба необходимо обратить внимание на то, что при сжатии длинных стержней бывают случаи
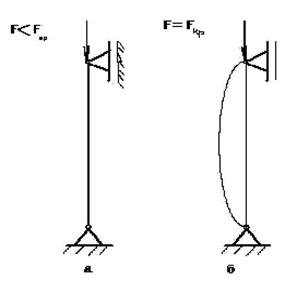
При изучении явления продольного изгиба необходимо обратить внимание на то, что при сжатии длинных стержней бывают случаи, когда при постепенном увеличении нагрузки резко меняется форма равновесия и напряженное состояние, в результате чего может быть внезапное разрушение. Если сжимающие силы будут больше предельной величины, то ось стержня изогнется, и стержень будет подвергаться, кроме сжимающей силы, изгибающему моменту (рисунок 38 а, б).
Рисунок 38- Продольный изгиб
где F – действующая на стержень сжимающая сила, Fкр – критическая сила, т.е. сжимающая центрально приложенная сила, при которой стержень еще устойчиво сохраняет прямолинейную форму равновесия. Величина критической силы определяется по формуле Эйлера:
где Е – модуль упругости 1 рода материала стержня, μ – коэффициент приведения длины стержня, Imin – наименьший осевой момент инерции сечения, ℓ - длина стержня, Fkp – величина критической силы. Зная величину критической силы Fkp и площадь сечения стержня А, можно определить величину критического напряжения:
так как
Нужно обратить особое внимание на предел применимости формулы Эйлера
где a и b – коэффициенты, зависящие от материала. Следует также четко представлять себе, что при расчетах на устойчивость в отличие от расчетов на прочность предельное напряжение (здесь – критическое напряжение σкр) зависит не только от материала бруса, но и его геометрических размеров, формы сечения, а также от способа закрепления концов. В обоих случаях λ</>λпред расчет стержня на продольный изгиб можно вести при помощи коэффициента понижения допускаемого напряжения на простое сжатие. Расчетная формула имеет вид:
|

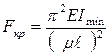 , (11)
, (11) , (12)
, (12) представляет собой радиус инерции сечения и
представляет собой радиус инерции сечения и - есть гибкость стержня, то величина критического напряжения выражается формулой:
- есть гибкость стержня, то величина критического напряжения выражается формулой: (13)
(13) . При гибкости, меньше предельной формула Эйлера неприменима, расчет стержня на устойчивость выполняют по эмпирической формуле Ясинского
. При гибкости, меньше предельной формула Эйлера неприменима, расчет стержня на устойчивость выполняют по эмпирической формуле Ясинского (14)
(14) , коэффициент φ зависит от гибкости и материала стержня.
, коэффициент φ зависит от гибкости и материала стержня.


