Практическая часть. Задача 1.Дано: N=26л.с.; n=360 об/мин; а=1.2м; в=0.6м; с=1.1м; D1=450cм; D2=400см; .
Задача 1. Дано: N=26л.с.; n=360 об/мин; а=1.2м; в=0.6м; с=1.1м; D1=450cм; D2=400см; Определить: Определить моменты, приложенные к шкивам; Определить окружные усилия; 3) Определить силы, изгибающие вал в горизонтальной и вертикальной плоскостях, и строить эпюры изгибающих моментов; 4) Построить эпюру суммарных изгибающих моментов; 5) Определить опасные сечения и величины максимального расчетного момента по третьей теории прочности. Решение: 1) Определение моментов, приложенных к шкивам. Момент на шкивах по передаваемой мощности и скорости вращения вала определяется по формуле
где N - передаваемая валом мощность, Вт,
Угловую скорость можно вычислить по формуле
Вычисляем момент на первом шкиве:
Моменты на втором и третьем шкивах будут одинаковыми и равны половине момента первого шкива
Построим эпюры крутящих моментов. 2) Определение окружных усилий (рисунок 35).
Спроектируем усилия
Рисунок 35 – Окружные усилия
3) Определяем силы, изгибающие вал в горизонтальной и вертикальной плоскостях, и строим эпюры изгибающих моментов. Рассматриваем изгиб вала в плоскости ZOX.
Проверка: Рассматриваем изгиб вала в плоскости YOZ.
Проверка: 4) Построим эпюру суммарных изгибающих моментов Находим суммарный момент по формуле:
5) Определение опасного сечения и величины максимального расчетного момента по третьей теории прочности. Из эпюр
5) Условие прочности вала по третьей теории прочности определяется по формуле
где
Принимаем диаметр вала:
Рисунок 36-Эпюры внутренних силовых факторов при сложном сопротивлении Задача 2. Дано:
Рисунок 37 – Ломанный стержень
1) построить эпюры 2) Расчет напряжений и определение размеров поперечных сечений стержней
Вопросы для самопроверки
1 Какой случай изгиба называется косым изгибом? 2 Возможен ли косой изгиб при чистом изгибе? 3 В каких точках поперечного сечения возникают наибольшие напряжения при косом изгибе? 4 Как определяются деформации при косом изгибе? 5 Может ли балка круглого поперечного сечения испытывать косой изгиб? 6 Как находят напряжения в произвольной точке поперечного сечения при внецентренном растяжении или сжатии? 7. Чему равно напряжение в центре тяжести поперечного сечения при внецентренном растяжении или сжатии? 8 Какие напряжения возникают в поперечном сечении стержня при изгибе с кручением? 9 Как находятся опасные сечения стержня при изгибе с кручением? 10 В каких точках круглого поперечного сечения возникают наибольшие напряжения при изгибе с кручением? 11 Как пишутся условия прочности стержня по всем четырем теориям, если известны sии tк? 12 Как находится величина расчетного момента при изгибе с кручением стержня круглого поперечного сечения? 13 По какой теории прочности (3 или 4) получится большая величина расчетного момента при заданных величинах Мии Мк?
|

 .
. ,
,
 – угловая скорость вращения вала, рад/с.
– угловая скорость вращения вала, рад/с.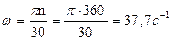


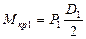
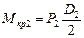
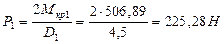
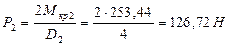
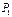 и
и  на координатные оси
на координатные оси  и
и  :
:

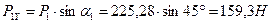
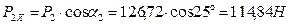
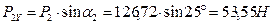





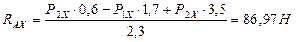
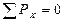




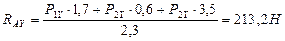

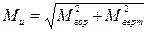
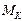 и
и  видно, что опасное сечение будет в точке C, где
видно, что опасное сечение будет в точке C, где  ;
; 

 ,
, - осевой момент сопротивления сечения. Для круга:
- осевой момент сопротивления сечения. Для круга:

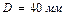

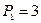
 ,
, 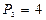

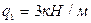 ,
, 
 ,
,  . Допускаемое напряжение на растяжении – сжатии
. Допускаемое напряжение на растяжении – сжатии  = 160 МПа. Первый стержень длиной
= 160 МПа. Первый стержень длиной  м имеет прямоугольное сечение с отношением сторон
м имеет прямоугольное сечение с отношением сторон 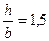 , второй (
, второй ( м) и третий (
м) и третий ( м) – круглое сечение.
м) – круглое сечение.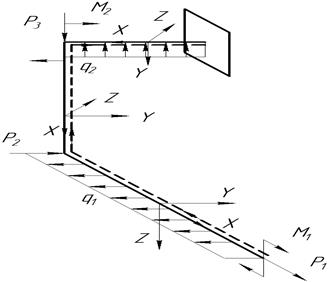
 ,
,  ,
,  ,
, 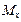 ,
, 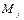 и
и 



