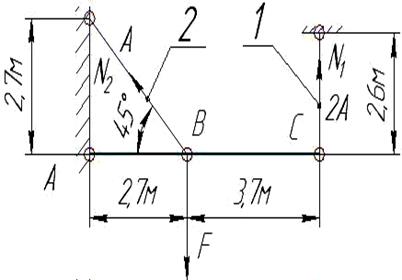
Практическая часть. Задача 1.Ступенчатый стержень круглого поперечного сечения нагружен силами
Задача 1. Ступенчатый стержень круглого поперечного сечения нагружен силами Определить: 1 Необходимые размеры попречных сечений бруса; 2 Нормальные напряжения; 3 Перемещения поперечных сечений. Решение: 1 Построим эпюры продольных сил. Схема нагружения стержня представлена на рисунке 6. Обозначим сечения, в которых приложены силы и меняются размеры стержня буквами, начиная от А до F. Сечениями, где приложены силы, стержень разбивается на три участка, в пределах которых продольная сила постоянная, поэтому для определения ее значений нужно рассечь каждый участок и из условия равновесия отсеченной части, не содержащей заделку, определить величину продольной силы. Проведем на участке АВ произвольное сечение I-I, отбросим часть стержня, содержащую заделку, и рассмотрим условие равновесия оставшейся правой части. На рассматриваемую часть стержня действует сила Р3 = 20кН и продольная сила N1 в сечении I-I. При определении продольных сил в сечениях предполагаем, что они растягивают рассматриваемую часть стержня, т.е. направлены от сечения. Проектируя силы на ось Х, получим N1 - Р3 = 0. Откуда N1 =Р3 =20 кН. Т.к. продольная сила N1 получилась с положительным знаком, то участок стержня АВ растягивается. Проведем произвольное сечение II-II и рассмотрим равновесие отсеченной части стержня, не содержащей заделку.
N2 +Р2 - Р3 = 0 N2 = -Р2 + Р3 =20 -10 = 10 кН. Положительный знак продольной силы N2 свидетельствует о том, что третий участок испытывает растяжение. Проведем произвольное сечение III-III и рассмотрим равновесие отсеченной части стержня, не содержащей заделку.
N3 - Р1 +Р2 - Р3 = 0 N3 = Р1 - Р2 + Р3 =40 - 10 + 20 = 50 кН.
Рисунок 6 - Схема нагружения стержня Положительный знак продольной силы N3 свидетельствует о том, что третий участок испытывает растяжение. По найденным значениям продольных сил строим график (эпюру) изменения продольных сил по длине стержня. Проводим базу эпюры параллельно оси стержня и в выбранном масштабе откладываем вверх положительные значения продольных сил и вниз отрицательные. При правильно построенной эпюре продольных сил в сечениях, где приложены сосредоточенные силы на эпюре будут иметь место скачки на величину приложенной силы. 2 Определим необходимые размеры попречных сечений бруса. Необходимые размеры поперечних сечений бруса определим исходя из условии прочности при растяжении.
Определим площади сечений на каждом участке
Значение напряжений на каждом участке
Выразим диаметр на участке где продольные силы имеют большее значение.
Округляем диаметры до ближайшего целого большего числа.
3 Построение эпюр нормальних напряжений.
По этим данным строим эпюру нормальных напряжений. 4 Построение эпюры перемещений поперечных сечений. Деформация бруса на каждом участке:
Перемещения в сечениях:
4 Определим необходимую толщину и диаметр головки стержня:
На срез ось рассчитываем по формуле:
На смятие ось рассчитываем по формуле:
Принимаем диаметр головки стержня D=41мм; Принимаем толщину головки стержня h=8мм. Задача 2. Дано: l=1м; l/L=0.3; С/L=0,52; λ/L=0,6; F1/F=1,2; F2/F=1,2; Р1/Р=3; Р2/Р=4; Определить: N, σ, ΔL.
Рисунок 7 – Схема нагружения стержня
Задача 3. Дано: Раскрыть статическую неопределимость стержневой системы. Решение:
Рисунок 8 - С татически неопределимая стержневая система Вопросы для самопроверки 1 Как можно нагрузить прямой брус, чтобы он работал только на растяжение (сжатие)? 2 Какие внутренние силовые факторы возникают в поперечном сечении стержня при его растяжении или сжатии? 3 Как строится эпюра продольных сил? 4 Что такое продольная и поперечная деформация бруса при растяжении (сжатии) и какова зависимость между ними? 5 По какой формуле определяется величина напряжения в поперечном сечении стержня? 6 Сформулируйте закон Гука и приведите формулу, выражающую этот закон.
|
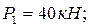
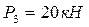. Принимаем материал стержня 
, 
, 
.
,
;
; 
; 
.
; 
; 
; 
; 
; 
.
;
;
;
.
; 
; 
; 
.
;
;
;
;
;
.
;
;
;
;
.
;
;
;
;
;
; 
;
;
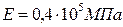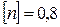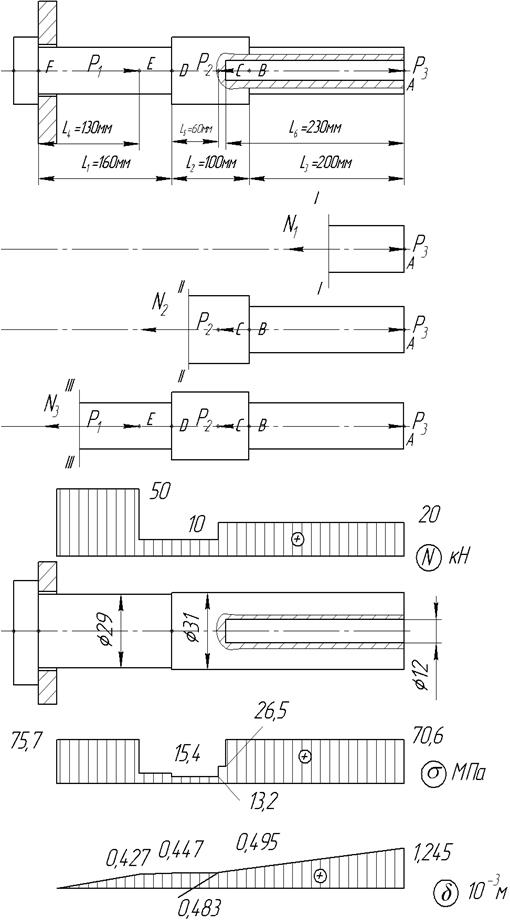
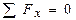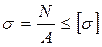
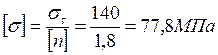
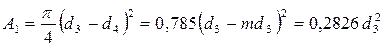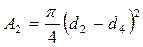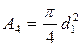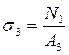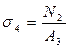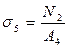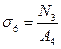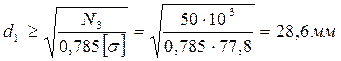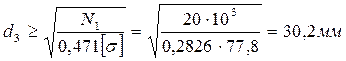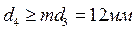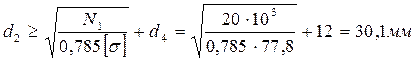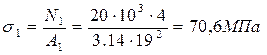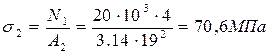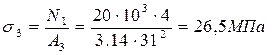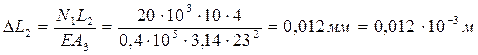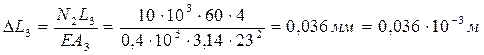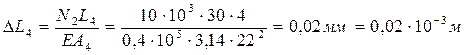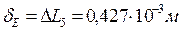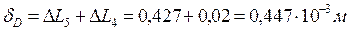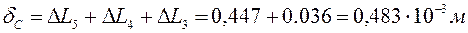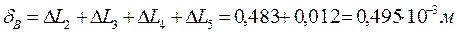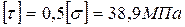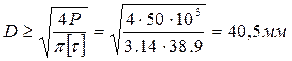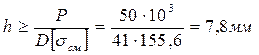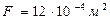; Р=10 кН; Е=1×105 МПа.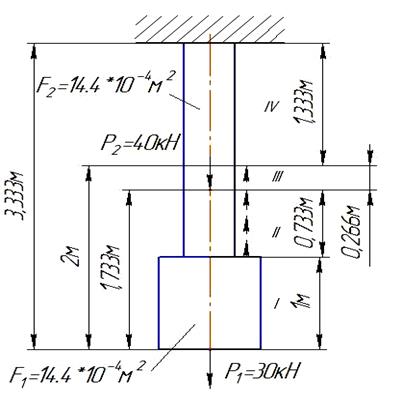
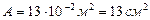; а=2,7м; b=3.7м; с=1,3м; α=45°; [σ]=160МПа; 
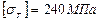; n=1,5.
