Теоретическая часть. Изучение темы необходимо начинать с выяснения вопроса о внутренних силовых факторах, действующих в сечении бруса
Изучение темы необходимо начинать с выяснения вопроса о внутренних силовых факторах, действующих в сечении бруса. Применение метода сечений позволяет найти величину и направление равнодействующей внутренней (продольной) силы упругости в рассматриваемом сечении. Принято считать, что внутренняя растягивающая сила положительна, а сжимающая – отрицательна. Поэтому неизвестную продольную силу N всегда направляют от сечения (рисунок 4), предполагая, что в рассматриваемом сечении возникает растяжение. Величина продольной силы N определяется из условия равновесия отсеченной части, а именно: сумма сил, действующих по оси х, равна нулю при условии равновесия бруса.
Рисунок 4- Направление продольной силы N
SFix=F-N=0, и следовательно N=F. Если при расчете продольная сила получается положительной, это значит, что она действительно направлена от сечения и является растягивающей. Если N получается отрицательной, то она является сжимающей. При изучении растяжения и сжатия прямого бруса следует обратить особое внимание на гипотезу плоских сечений, которая справедлива и при других видах нагружения бруса. Сущность ее заключается в том, что плоские сечения, нормальные к оси бруса до деформации, остаются и после деформации плоскими и нормальными к его оси, а отсюда следует, что продольные элементы бруса растягиваются одинаково, силы упругости будут распределяться по сечению бруса равномерно, а поэтому напряжение во всех точках сечения определяется по формуле
где N – внутренняя сила; А – площадь поперечного сечения, которая является геометрической характеристикой прочности и жесткости, форма сечения значения не имеет, все точки сечения равноопасны. Мерой деформации растяжения (ε) является относительное удлинение (рисунок 5).
Рисунок 5- Удлинение бруса
где ℓ – первоначальная длина бруса; Δℓ=ℓ1- ℓ – абсолютное удлинение. Величина ε не имеет размерности и часто выражается в процентах. Особого внимания заслуживает закон Гука, согласно которому в пределах упругой деформации материала между напряжением и деформацией принимается прямо пропорциональная зависимость, которая выражается формулой:
где σ – нормальное напряжение; Ε – модуль продольной упругости (модуль упругости первого рода или модуль Юнга); ε - относительное удлинение (или осевое укорочение). Модуль продольной упругости имеет размерность напряжения МПа или Па, (1 МПа = 106 Па) и характеризует жесткость материала, его способность сопротивляться упругому деформированию. Для участка бруса длиной l, на котором постоянны продольная сила и площадь поперечного сечения, закон Гука можно записать в виде:
Это вторая форма закона Гука. Произведение ЕА называют жесткостью сечения. При расчетах на растяжение и сжатие используют основной принцип прочности детали: действующие или расчетные напряжения ни в одной точке детали не должны превышать допускаемые напряжения. Так как при растяжении (сжатии) во всех точках сечения напряжения одинаковы, то при расчете бруса на прочность определяют положение наиболее напряженного (опасного) поперечного сечения. Если брус имеет постоянное по его длине поперечное сечение, то опасным является сечение, в котором возникает наибольшая продольная сила N. Если значение продольной силы во всех сечениях одинаково, то опасным является сечение с наименьшей площадью. Для определения опасного сечения бруса при изменяющихся по его длине площади поперечного сечения и продольной силе необходимо строить эпюру нормальных напряжений. Условие прочности бруса при растяжении (сжатии), составленное для опасного сечения, имеет вид:
Условие прочности в словесной форме можно записать следующим образом:
Форма сечения бруса не влияет на его прочность при растяжении (сжатии). Форму сечения бруса необходимо знать только для определения размеров сечения при известном сечении площади. С помощью условия прочности выполняют три вида расчетов: проверочный расчет, проектный расчет и определение допускаемой нагрузки. Надо знать, что в ряде случаев необходимые для расчета бруса усилия невозможно найти только из уравнений равновесия. Такие задачи называют статически неопределимыми. При решении таких задач уравнения, которых не хватает для определения усилий, составляют из условия деформации бруса или системы.
|


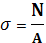 ,
,
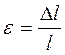
 , (1)
, (1) (2)
(2)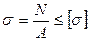 (3)
(3)


