Другие виды средних показателей
- хронологическая средняя - антигармоническая средняя - средняя ошибка выборки - и др. Степенные средние величины получили свое название по виду функции, используемой для их расчета. Если значения признаков в статистической совокупности не повторяются, степенную среднюю величину Простая степенная средняя величина рассчитывается по формуле
где k – показатель степени средней величины. При k = - 1 по данной формуле рассчитывают гармоническую среднюю величину (
Далее при k = 1 находят арифметическую среднюю, при k = 2 - квадратическую, при k = 3 - кубическую, при k = 4 - биквадратическую и т.д. Если одно и то же значение признака встречается несколько раз, рассчитывают взвешенную среднюю величину:
где f Гармоническая средняя применяется если: 1) осредняемый признак является мерой времени и выражен в секундах и минутах. 2) осредняемая величина задана в виде функции неявного вида. 3) осредняемые значения признака имеют общий показатель (например, один и тот же путь, пройденный автомобилями с разной скоростью является общим показателем при расчете средней скорости автомобиля)
где n – количество единиц в совокупности.
где М Геометрическая средняя применяется при нахождении средних темпов или коэффициентов роста, т. к. она показывает восколько раз в среднем одна величина в упорядоченной совокупности больше (или меньше) другой.
где n – число сомножителей (осредняемых значений признака).
Арифметическая средняя определяется по формулам:
Квадратическая средняя используется в тех случаях, когда осредняемая величина xi задана в виде квадратической функции.
Кубическая средняя применяется, если осредняемая величина задана в виде кубической функции.
Биквадратическая средняя рассчитывается как степенная средняя четвертого порядка и применяется при осреднении признака, являющегося функцией четвертого порядка.
3.5 Средние показатели структуры
Мода (Мо) — это наиболее часто встречающееся значение признака в статистической совокупности или значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по разному. В дискретных вариационных рядах мода – это признак, которому соответствует наибольшая частота. В зависимости от того, равны интервалы между собой или нет, применяют тот или иной подход к определению моды. Для определения моды в интервальных вариационных рядах с равными интервалами сначала по наибольшей частоте находят модальный интервал, затем рассчитывают моду по формуле:
где
Для получения более полной характеристики вариационного ряда помимо средней величины и моды рассчитываются так называемые структурные показатели. К ним относятся медиана, квартили, децили и перцентили. Медианой (Me) является значение варианты, находящейся в центре упорядоченных по возрастанию/убыванию значений признака совокупности. Медиана делит вариационный ряд на две равные части. При этом 50% единиц совокупности имеют значение меньше медианного, а 50% - больше медианного. В дискретном ряду распределения медиана находится по номеру. Номер медианы находится по формуле:
где n – число единиц в совокупности. При четном количестве единиц в совокупности медиана получается путем расчета средней арифметической из двух рядом стоящих значений признаков. В интервальном ряду распределения медиана рассчитывается по формуле:
где
Медиана имеет свойство, благодаря которому используется в экономических и коммерческих расчетах:
В нормальных рядах распределения мода и медиана совпадают со средним арифметическим значением. Квартили, квинтили, децили иперцентили относятся к группе квантилей. Квантили — это показатели, которые делят вариационные ряды на равные по численности единиц части. Квартили делят упорядоченный вариационный ряд на четыре равные части: первый квартиль является значением, которого не превышают 25% единиц совокупности, второй квартиль - 50% (он совпадает с медианой), третий— 75%. Квинтили делят упорядоченный вариационный ряд на пять равных частей, децили - на десять равных частей. Пятый децильсовпадает с медианой и вторым квартилем. Перцентили делят упорядоченный вариационный ряд на сто равных частей.
|

 вычисляют в простой форме - это простая степенная средняя, при повторяющихся значениях – во взвешенной форме. Количество повторяющихся значений одного и того же признака (Х i) называется его весом (f
вычисляют в простой форме - это простая степенная средняя, при повторяющихся значениях – во взвешенной форме. Количество повторяющихся значений одного и того же признака (Х i) называется его весом (f  ).
). = (
= (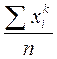 )
) 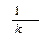 , (3.8)
, (3.8) Если k 0, на основе теории пределов по данной формуле определяют геометрическую среднюю величину (
Если k 0, на основе теории пределов по данной формуле определяют геометрическую среднюю величину (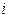
 f
f 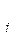 ) / ∑ f
) / ∑ f  ).
).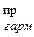 =
=  , (3.10)
, (3.10)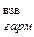 =
= 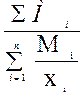 , (3.11)
, (3.11) = x
= x 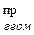 =
= 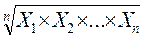 , (3.12)
, (3.12)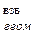 =
=  (3.13)
(3.13) (3.14)
(3.14)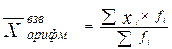 (3.15)
(3.15)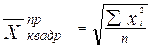 (3.16)
(3.16) (3.17)
(3.17)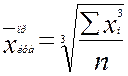 (3.18)
(3.18)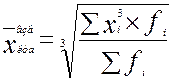 (3.19)
(3.19)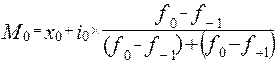 , (3.20)
, (3.20)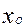 – начало модального интервала,
– начало модального интервала, – длина модального интервала,
– длина модального интервала,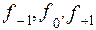 – частоты интервалов, стоящих перед модальным, модального и после модального.
– частоты интервалов, стоящих перед модальным, модального и после модального.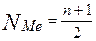 , (3.21)
, (3.21) , (3.22)
, (3.22)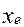 - начало медианного интервала,
- начало медианного интервала, – длина медианного интервала,
– длина медианного интервала,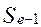 –накопленная частота до интервала, в котором находится медиана,
–накопленная частота до интервала, в котором находится медиана,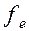 – частота медианного интервала.
– частота медианного интервала.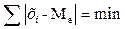 (3.23)
(3.23)


