Статистические методы анализа взаимосвязей социально-экономических явлений
Между социальными и экономическими явлениями имеется два основных типа связи — функциональная и корреляционная. В соответствии с этим подходом все признаки подразделяют на зависимые и независимые. Независимыми, или факторными, называют признаки, которые вызывают изменения других, связанных с ними признаков. Зависящие от них признаки называют результативными. При функциональной связи между признаками имеется взаимнооднозначное соответствие, то есть одному значению факторного признака соответствует одно и только одно вполне определенное значение результативного признака и наоборот. Например, взаимосвязь между длиной радиуса и окружности. Функциональные связи проявляются с одинаковой силой и полнотой у всех единиц совокупности. При корреляционной связи каждому значению независимого признака может соответствовать множество значений зависимой переменной и наоборот. Такие связи проявляются лишь в среднем как закономерность, то есть под действием закона больших чисел. Установление типа связей необходимо для определения метода их исследования, поскольку для разных типов связей применяют различные методы их исследования. Функциональные связи изучаются с помощью балансового и индексного метода. Балансовый метод состоит в проверке равенства.
Рис 2 Взаимосвязи в балансовом методе анализа
По величине известных любых трех компонентов этого равенства можно определить (проверить) значение четвертого. Индексный метод - это метод изучения величины сложных совокупностей и отдельных их единиц. При этом под сложной понимается статистическая совокупность, отдельные элементы которой непосредственно не подлежат суммированию во времени и пространстве. в текущем и базисном периоде. Если целью анализа является определение объема товарооборота при продаже в предстоящем периоде такого же количества товаров, что и в базисном периоде, но по новым ценам, то применяется агрегатный индекс цен Э. Ласпейреса. Если при определении индекса цен исходная информация содержит лишь данные о количестве товаров в базисном и текущем периодах, то средняя их величина определяется методом средней взвешенной. Между индексами определенных величин сохраняются такие же соотношения, как и между исходными величинами. Например, если с = a * b, то I c = I a* I b . Если с = a / b, то I c = I a / I b. Взаимосвязанные индексы применяются для изучения влияния структурных сдвигов на изменение социально-экономических явлений. На изменение средней величины оказывает влияние как изменение значений осредняемого признака хi, так и изменение структуры статистической совокупности, обусловленное изменением численности отдельных вариантов изучаемой совокупности fi. Влияние изменения каждого фактора в отдельности, то есть осредняемого признака хi и структуры совокупности fi, может быть изучено с помощью индексного анализа:
Iх * fi = I хi * I fi (4.2) Стохастические (корреляционные) связи. Стохастические связи проявляются в виде корреляции между значениями. Для их изучения применяются 1. графический метод, 2. метод сравнения параллельных рядов, 3. метод аналитических группировок, 4. регрессионно-корреляционный анализ (РКА). Регрессионный анализ позволяет выявить вид связи, а корреляционный - установить тесноту (силу) связи. Для линейных зависимостей теснота связи определяется с помощью коэффициента корреляции, а для нелинейных - с помощью индекса корреляции (корреляционного отношения). Индекс корреляции является более универсальным показателем по сравнению с коэффициентом. Для расчета коэффициента корреляции используются различные формулы, но все они выводятся из одной и той же формулы.
где s х и s у - среднеквадратические отклонения Х и У, рассчитанные по сгруппированным данным:
s х = ± ; (4.4) å f k
å (У k – У общ)2 * f k s у = ±. (4.5) å f k
Теоретическое корреляционное отношение рассчитывают по формуле:
h = ± å (УХ k – У общ)2 * f k, (4.6) å (У k – У общ)2 * f k
где УХ k - выравненные значения результативного признака, то есть рассчитанные по уравнению регрессии при Х = X к. Значения r,h находятся в пределах от -1 до +1 -1 Чем ближе значение r, h к единице, тем теснее связь между факторами х и у. Если эти значения < 0, это говорит об обратной связи между факторами х и у. Если х и у = 0, то связь между ними отсутствует. Если эти значения > 0, это говорит о прямой связи между факторами х и у. Чтобы определить тесноту связи пользуются таблицей Чэддока. При r = Корреляционное отношение являются более универсальным показателем, его можно рассчитывать и для линейных связей. Для оценки тесноты связи между качественными показателями (например, работа по специальности, наличие жилья и т.п.) применяют непараметрические методы оценки корреляционной связи факторов. К непараметрическим методам относятся оценка связи на основе расчета коэффициентов ассоциации и контингенции. Для этого предварительно составляют таблицу, на пересечении строк и столбцов которой находятся числа, равные количеству единиц статистической совокупности с соответствующими значениями первого и второго признака.
Таблица 1 – Таблица значений качественных признаков
По итоговым данным таблицы 1 рассчитывают коэффициент ассоциации либо коэффициент контингенции:
Если эти коэффициенты < 0.3, то связи между признаками нет. Преимущество первого показателя состоит в том, что он единственный из всех показателей тесноты связи вполне определенно позволяет ответить на вопрос о характере связи между двумя признаками (прямопропорциональна она или обратнопропорциональна). Зависимость между признаками может быть парной и многофакторной. В последнем случае на один и тот же признак у, оказывает влияние несколько факторных признаков, т.е.
|


 , (4.3)
, (4.3) å (Х k – X общ)2 * f k
å (Х k – X общ)2 * f k


 1 - связь функциональная.
1 - связь функциональная.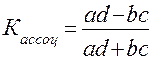 , (4.7)
, (4.7) . (4.8)
. (4.8) .
.


