Определение опасного загружения и опасного сечения от подвижной системы сосредоточенных сил
Максимальное значение изгибающего момента в сечении х = а (рис. 19) от подвижной системы грузов будет иметь место тогда, когда одна из сил подвижной системы расположена над вершиной линии влияния. Эту силу называют критической. Допустим, что система грузов стоит по отношению к сечению x = а в положении, дающим опасное загружение Мизг = Мах. Тогда смещение системы грузов на D x из этого положения вправо (D x ® 0) или влево (D x < 0) должно в обоих случаях вызывать уменьшение изгибающего момента, т.е. D М < 0. Изгибающий момент при первоначальном положении системы
а после смещения ее на D x
Тогда приращение момента
а так как то
Приращение момента DМизг может быть отрицательным только тогда, когда сомножители выражения (12) имеют разный знак, т.е. соблюдаются неравенства: при D x > 0 при D x < 0 Эти неравенства служат для проверки того, является ли данная сила системы грузов, стоящая над вершиной линии влияния, действительно критической, а положение грузов самым опасным.
Пример 1. Определить, при каком положении грузов система сил, изображенная на рис. 20 а, вызовет максимальный момент посредине пролета балки, если Р1 > Р2. Решение. Поставим систему грузов так, чтобы сила Р2 была над вершиной линии влияния (рис. 20 б) и проверим по неравенствам (13), является ли такое положение грузов опасным. Учитывая, что углы a1 и a2 находятся в разных четвертях, При D x < 0 при D x > 0; Одно из неравенств (13) не соблюдается, значит Р2 не является критической силой, а принятое положение грузов – не самое опасное. Передвинем систему грузов так, чтобы над вершиной стала сила Р1 (рис. 20 в). Тогда проверка даст: при D x > 0 - при D x < 0 Неравенство (13) соблюдается, значит груз Р1 является критическим. Положение опасного сечения на конструкции не всегда бывает известно, что усложняет определение опасных загружений от подвижной системы сил. Тогда поступают на основе следующих соображений.
Рис. 20 Рис. 21
Предположим, что координата опасного сечения равна х (рис. 21). Построим линию влияния для этого сечения. Найдем равнодействующую системы сил R по величине и расположению (рис. 21) и через нее выразим опорную реакцию RА, затем определим изгибающий момент в сечении x:
Максимальное значение Мх будет тогда, когда
где l – длина пролета; d – расстояние равнодействующей силы от критической. Для определения опасных сечений и загружения применяют следующую последовательность работы: - находят величину и положение равнодействующей системы грузов R; - предположительно принимают одну из сил системы за критическую и определяют величину d; - находят положение опасного сечения - строят линию влияния момента для опасного сечения; - находят опасное загружение для сечения x 1, для чего ставят систему так, чтобы сила, принятая за критическую, была над вершиной линии влияния; - проверяют по неравенствам при - если неравенства удовлетворяются, ищут расчетный изгибающий момент (опасное загружение). Если неравенства не удовлетворяются, повторяют всю работу сначала. Принимают другую силу за критическую, ищут новое расстояние d и т. д.
Пример 2. Определить опасное сечение, опасное загружение и требуемый момент сопротивления балки, нагруженной подвижной системой грузов (рис. 22). Решение. Находим величину и положение равнодействующей силы (рис. 22 а). R = 3 + 2 + 4 = 9 тс. Для определения положения равнодействующей силы берем момент относительно точки Д.
Отсюда
Предположительно принимаем за критическую самую большую силу Определим положение опасного сечения.
Теперь строим линию влияния М для сечения x = 7 (рис. 22 б) и ставим силу Р3 над вершиной линии влияния. Определяем ординаты линии влияния под силами Р3, Р2, Р1. Проверяем, правильно ли выбрана критическая сила по неравенству (13), для чего находим
при D x > 0
Рис. 22
Проверка показала не соблюдение условий неравенства (13). Следовательно, критическая сила выбрана неправильно. Возьмем в качестве критической силы Строим новую линию влияния (рис. 22 в) и определяем ординаты линии влияния.
Проверяем правильность выбора критической силы, для чего находим
при D x > 0 при D x < 0 Контрольные неравенства соблюдены, следовательно, сила Максимальный момент
Если [s] = 1600 кгс/см2, то требуемый момент сопротивления
Отыскание расчетных (максимальных) усилий в балке усложняется при необходимости одновременного учета усилий от нагрузок: неподвижных На практике поступают таким образом: - разбивают пролет балки на 10-12 равных участков и строят для каждого сечения линии влияния (0,1 l; 0,2 l; 0,3 l …); - для каждого сечения определяют опасное загружение от подвижной системы сил и находят максимальное усилие в данном сечении от системы подвижных грузов; - пользуясь теми же линиями влияния, определяют в каждом сечении усилия от подвижных сосредоточенных нагрузок - строят обобщенную диаграмму максимальных суммарных усилий от всех видов нагрузки в каждом сечении
Фермы
|

 (9)
(9) (10)
(10) , (11)
, (11) ,
,
 . (12)
. (12) ;
; . (13)
. (13)
 .
. ;
; .
. ;
; .
.
 ;
;  ;
; . (14)
. (14) ;
;  ; (15)
; (15) ;
;  ; (16)
; (16) ,
, ;
;
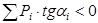 ; и при
; и при 
 , правильно ли выбрана критическая сила;
, правильно ли выбрана критическая сила;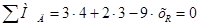 .
. м.
м. м.
м. ;
;  ,
, .
.
 .
.

 .
. ;
; 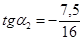 ,
,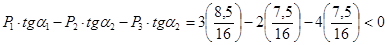 ;
; .
. – критическая.
– критическая. тс×м.
тс×м.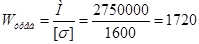 см2.
см2.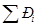 , подвижных сосредоточенных
, подвижных сосредоточенных  и распределенных
и распределенных  . Использовать описанный выше аналитический путь для определения опасного сечения невозможно, так как подвижные нагрузки
. Использовать описанный выше аналитический путь для определения опасного сечения невозможно, так как подвижные нагрузки  ; от распределенных нагрузок
; от распределенных нагрузок  ;
;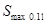 ,
,  и т.д. В качестве расчетного принимают самое большое из максимально возможных усилий. Под S следует понимать любое из усилий М, Q или N.
и т.д. В качестве расчетного принимают самое большое из максимально возможных усилий. Под S следует понимать любое из усилий М, Q или N.


