Использование линий влияния для определения усилий в заданном сечении от системы сосредоточенных и распределенных неподвижных нагрузок
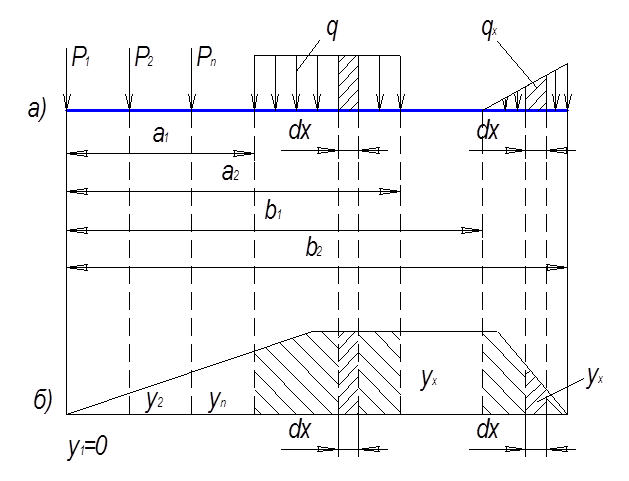
Пусть на сооружение действует нагрузка, состоящая из нескольких параллельных сосредоточенных сил Р1, Р2, Рn и распределенной нагрузки с интенсивностью q. Требуется определить влияние этой нагрузки на некоторую величину Z (это может быть изгибающий момент М, поперечная сила Q или продольное усилие N), для которой линия влияния известна (рис. 16 б).
Рис. 16
Ординаты линии влияния у1, у2, уn выражают величину усилия в исследуемом сечении от единичного груза, стоящего над соответствующей ординатой. Если над данной ординатой у1 стоит не единичный груз, а груз Р1, то усилие в исследуемом сечении от груза Р1 будет у1Р1, от груза Р2 – у2Р2, от груза Рn – уnРn. Подобные рассуждения справедливы для любого количества сосредоточенных сил. Распределенную нагрузку можно представить как совокупность элементарных сосредоточенных сил qdx. Каждая элементарная сила вызывает в исследуемом сечении усилие ухqdx. Для равномерно распределенной нагрузки q = const, а для треугольной распределенной нагрузки интенсивность ее зависит от x. Общее усилие в исследуемом сечении от любой системы нагрузок равно сумме усилий от отдельных сосредоточенных сил и распределенных нагрузок, т.е.
где
Учитывая, что q = const, а
где w – площадь, ограниченная линией влияния и расположенная под нагрузкой (на рис. 16 б заштрихована). В большинстве случаев можно пользоваться формулой с двумя первыми членами, так как в практике редко встречаются нагрузки, распределенные по сложному закону:
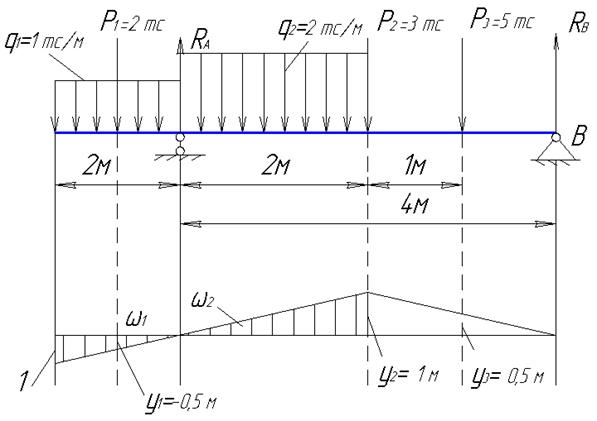
где n и m – количество сосредоточенных сил и распределенных нагрузок. Примечания: - если направление нагрузки совпадает с направлением единичного груза, от которого построена линия влияния, то соответствующее слагаемое записывается в формулу (8) со знаком «плюс». Если эти направления противоположны друг другу, то соответствующее слагаемое записывается со знаком «минус»; - ординаты линии влияния уi записываются со своими знаками; - если площадь w состоит из разных участков с разными знаками, то под величиной w понимается алгебраическая сумма площадей этих участков; - формула (8) применяется только в тех случаях, когда расчетная схема конструкции допускает применение принципа независимости действия сил (на основании принципа независимости сил влияние всей совокупности сил будет равно: Пример 1. Определить с помощью линий влияния изгибающий момент посредине пролета балки от системы нагрузок (рис. 17).
Рис. 17
Решение. Строим линию влияния Ма =2 для сечения посредине пролета. Под левой опорой откладываем a = 2 м. Ординаты под сосредоточенными грузами определяем из подобия треугольников: у1 = -0,5 м; у2 = -1,0 м; у3 = 0,5 м. Находим площади:
Общее усилие Изгибающий момент
Пример 2. У балки, изображенной на рис. 18, найти поперечную силу в сечении a = 1 м с помощью линии влияния. Решение. Строим линию влияния поперечной силы Qа=1 для сечения a = 1 м (рис. 18). Определяем величины ординат: Находим площади
Поперечная сила
|

 , (7)
, (7)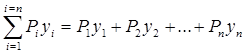 .
. ,
, ,
,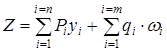 , (8)
, (8) ).
).
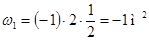 ;
; 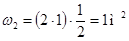 .
. .
. тс×м.
тс×м. ;
; 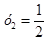 ;
; 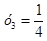 .
. ;
;  .
.
 тс×м.
тс×м.


