Линии влияния опорных реакций для двухконсольной балки
На рис. 8 показаны различные возможные положения единичной силы Р=1.

Рис. 8
В данном случае, как и в предыдущем примере для балки без консолей, уравнение линии влияния опорных реакций получается из уравнений равновесия всей балки. Благодаря непрерывности балки и изменения абсциссы точки приложения единичного груза получится одно и то же уравнение независимо от того, находится ли единичный груз между опорами (как и в предыдущем примере) или на консолях. В этом легко убедиться, рассмотрев уравнения равновесия балки при трех произвольных положениях единичного груза и учитывая при этом высказанные выше соображения относительно момента единичной силы при составлении уравнения равновесия. Например, для линии влияния опорной реакции RA будем иметь при начале координат в точке А (рис. 8 а) при расположении единичного груза на левой консоли
при расположении единичного груза между опорами балки
при расположении единичного груза на правой консоли балки
Таким образом, линия влияния опорной реакции Аналогично получится и для линии влияния реакции Вид уравнения этой прямой естественно будет зависеть от выбранной системы координат. Примем начало координат в точке 0 (рис. 8 б) и рассмотрим линию влияния реакции Уравнение равновесия балки записывается в виде (единичный груз между опорами):
Отсюда получаем уравнение линии влияния реакции При x 1 = m получим При x 1 = m + l получим Как видим, получена та же самая прямая, что и при начале координат в точке А. Аналогично получим уравнение для линии влияния RB:
При x 1 = m RB = 0; при x 1 = m + l RB = 1. Линии влияния опорных реакций с консолями показаны на рис. 8 в.
|

 , отсюда
, отсюда 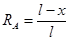 ;
;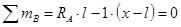 , отсюда
, отсюда  описывается одним и тем же уравнением на протяжении всей балки с консолями и справедливым при
описывается одним и тем же уравнением на протяжении всей балки с консолями и справедливым при  .
.
 :
:  , справедливое (как показано выше) на всем протяжении балки, т.е. при 0 £ x £ (m+ l +m).
, справедливое (как показано выше) на всем протяжении балки, т.е. при 0 £ x £ (m+ l +m). .
.


