Линии влияния изгибающих моментов и поперечных сил в поперечных сечениях простой балки
Для определения изгибающего момента и поперечной силы, являющихся внутренними усилиями в некоторых сечениях балки, необходимо использовать метод сечений, т.е. мысленно разрезать балку на две части по рассматриваемому сечению. Как указано в п.1.4 из уравнения равновесия одной из отсеченных частей балки (любой) получается уравнение линии влияния. При переходе единичного груза через рассматриваемое сечение резко меняются условия равновесия обеих отсеченных частей балки. Следовательно, при этом изменится и уравнение линии влияния, т.е. уравнения линии влияния слева от рассматриваемого сечения и справа от него будут разными.
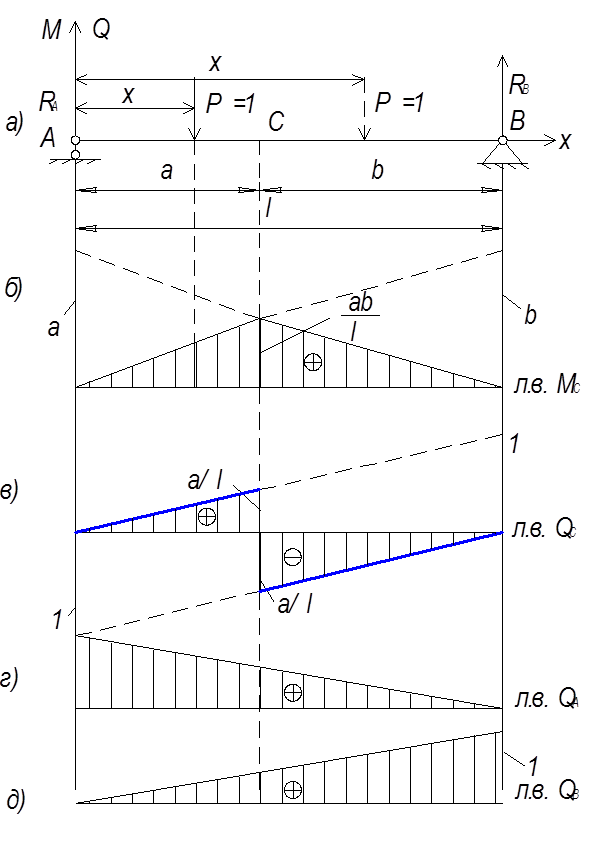
Рис. 9
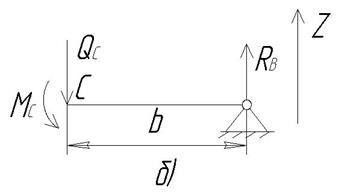
Рассмотрим порядок построения линий влияния изгибающего момента Выберем систему координат: начало в точке А; ось x, определяющую положение единичного груза, направим вправо; ось у ординат линии влияния Поставим единичный груз в произвольное положение – слева от сечения С и обозначим его положение абсциссой x (единичный груз может занимать любое положение от x = 0 до x = a, на рис. 9 он изображен сплошной линией). Считая единичный груз неподвижным в этом произвольном положении, определим изгибающий момент Для этого необходимо мысленно разрезать балку на две части по сечению С и отбросить одну из частей, а для оставшейся части составить уравнение равновесия, из которого и получится уравнение линии влияния. Примечания: - отбрасывать следует ту часть балки, на которую действует больше внешних сил; - уравнение равновесия следует выбрать такое, в которое войдет только одна неизвестная искомая величина Отбросим левую часть балки, а для оставшейся правой части (рис. 10 б) составим необходимое уравнение равновесия. Все усилия (
Рис. 10
Для определения
В него не войдет Для определения
В него не войдет Из этих уравнений получим При выбранной системе координат, как показано в п. 2.2.1, тогда Это и будут уравнения линий влияния МС и QC , справедливые для левой части балки (слева от сечения), т.е. при 0 £ x £ a. Границы справедливости уравнений устанавливаются из того, где находится единичный груз. Это уравнения прямых, для построения которых достаточно определить координаты двух их точек. Для при x = 0 при x = a По этим данным построены левые участки линий влияния Теперь поставим единичный груз в произвольном положении справа от сечения С, обозначим его положение абсциссой x (единичный груз – на рис. 9 показан пунктиром – может занимать любое положение от x = a до x = l) и определим После мысленного разреза балки по сечению “С” целесообразно отбросить правую часть балки. Уравнения равновесия для оставшейся левой части (рис. 8 а) будут иметь вид:
Из этих уравнений с учетом того, что при выбранной системе координат
Это тоже уравнение прямых. Найдем две их точки. Для при x = a при x = l По этим данным построены прямые участки линий влияния Полезно запомнить следующее: a и b – расстояния от рассматриваемого сечения соответственно до левой и правой опоры балки, и l – пролет балки; линия влияния изгибающего момента изображается отрезками двух прямых, пересекающихся под рассматриваемым сечением. Ордината точки их пересечения равна линия влияния поперечной силы изображается отрезками двух параллельных прямых. Ординаты их точек под рассматриваемым сечением равны Линии влияния QА и QВ, изображенные на рис. 9 г,д, аналогичны линии влияния QC (рис. 9 в), когда сечение «С» расположено сколько угодно близко к левой или правой опорам балки.
|

 и поперечной силы
и поперечной силы 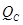 в некотором сечении С балки АВ (рис. 9 а).
в некотором сечении С балки АВ (рис. 9 а).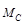 и
и 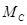 или
или  ), действующие на оставшуюся часть балки, должны быть изображены по их правилам знаков. Считаем момент положительным в том случае, когда он вызывает сжатие в верхнем волокне.
), действующие на оставшуюся часть балки, должны быть изображены по их правилам знаков. Считаем момент положительным в том случае, когда он вызывает сжатие в верхнем волокне.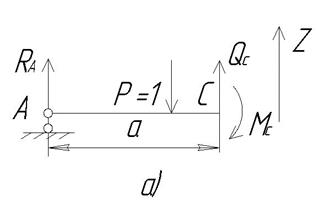
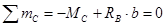 .
.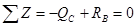 .
.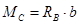 и
и 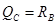 .
.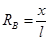 ,
, и
и 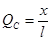 .
. . при x = a
. при x = a 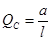 .
. ;
; 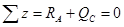 .
. (см. п. 2.2.1), получим уравнение линий влияния МС и QС, справедливые справа от сечения “С”, т.е. при a £ x £ l:
(см. п. 2.2.1), получим уравнение линий влияния МС и QС, справедливые справа от сечения “С”, т.е. при a £ x £ l: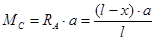 ;
; 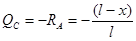 .
. ; при x = a
; при x = a  ;
;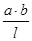 , а ординаты под опорами равны нулю. Продолжения этих прямых отсекают на вертикалях под опорами отрезки «a» слева и «b» справа;
, а ординаты под опорами равны нулю. Продолжения этих прямых отсекают на вертикалях под опорами отрезки «a» слева и «b» справа;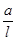 (для левого отрезка) и
(для левого отрезка) и 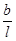 (для правого отрезка), а ординаты под опорами равны нулю. Продолжения этих прямых отсекают на вертикалях под опорами отрезки, равные единице.
(для правого отрезка), а ординаты под опорами равны нулю. Продолжения этих прямых отсекают на вертикалях под опорами отрезки, равные единице.


