Понятия о линиях влияния
Большинство стальных и других конструкций испытывает воздействие сложных систем сосредоточенных и распределенных нагрузок, положение которых на конструкции не является строго фиксированным, например, подвижных грузов. В зависимости от положения системы подвижных грузов на конструкции величина усилий в отдельных ее элементах или сечениях будет в общем случае различной. Для каждого сечения или элемента конструкции существует свое, чаще всего единственное, положение нагрузок, при котором данное сечение или элемент будут наиболее нагружены. Такое нагружение называется опасным и принимается в качестве расчетного при проверке прочности и работоспособности рассматриваемого элемента или сечения. Для определения опасных нагружений можно последовательно найти величины усилий в исследуемом сечении или элементе при разных положениях системы нагрузок. Максимальные значения усилий принимают в расчет для данного элемента или сечения. Однако такой путь трудоемок, особенно при больших количествах элементов конструкции и подвижных нагрузок. Эту задачу помогают решать линии влияния (инфлюэнтные линии), позволяющие значительно упростить и облегчить расчеты конструкций, работающих под воздействием подвижных нагрузок. Полезно сравнить линии влияния с эпюрами. Под эпюрами изгибающих моментов, поперечных сил, прогибов и т.д. для какого-нибудь стержня понимаются графики, изображающие закон изменения соответствующих величин по всему пролету этого стержня при действии заданной неподвижной нагрузки. Эпюра дает возможность увидеть сразу распределение интересующей нас величины по всем сечениям стержня, но только для одного, совершенно определенного, положения заданной нагрузки. Как изменятся эти величины при каком-нибудь ином расположении нагрузки, это из данной эпюры усмотреть невозможно. Для получения ответа пришлось бы построить новую эпюру. Линия влияния, наоборот, дает возможность увидеть сразу закон изменения какой-нибудь величины, относящейся к определенному сечению стержня, при всевозможных положениях единичного груза. Однако она ничего не говорит об изменении аналогичной величины, относящейся к другому сечению стержня. Нагрузку на расчетной схеме конструкции обычно представляют в виде сосредоточенных сил и распределенных (погонных) нагрузок. Распределенную нагрузку можно представить в виде совокупности сосредоточенных сил. Неподвижную сосредоточенную силу можно рассматривать как частное положение движущейся по конструкции подвижной сосредоточенной силы. Простейшей сосредоточенной силой является сила, равная единице, точка приложения которой перемещается по сооружению, в то время как сама сила сохраняет неизменное направление. Исходя из этого, представляется возможным на первом этапе исследовать влияние на искомую величину (усилие или перемещение) подвижной единичной сосредоточенной силы, а затем по определенному правилу, изложенному далее, установить влияние всех действующих на конструкцию нагрузок. При этом непременным условием является то, чтобы все действующие на конструкцию нагрузки и заменяющая их на первом этапе единичная сосредоточенная сила были параллельны друг другу, а расстояние между подвижными нагрузками сохранялись неизменными. Рассмотрим, например, балку (рис. 1 а), нагруженную движущейся по ней единичной сосредоточенной силой, сохраняющей неизменное направление. Координату точки ее приложения обозначим буквой х.
 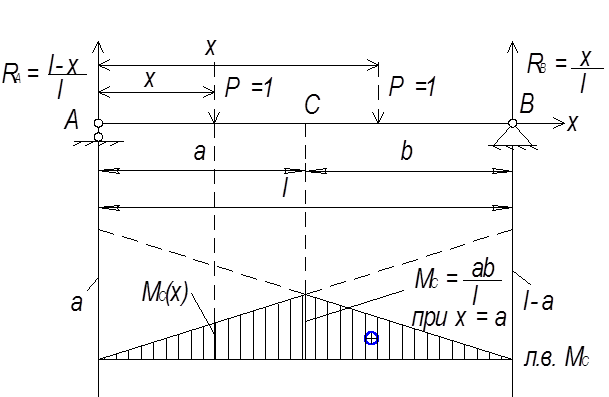
Рис. 1
Определим влияние этой силы на изгибающий момент МС в сечении С. Когда единичная сила находится между точками С (х = а) и В (x = l), то в равновесии рассматриваем левую часть. Изгибающий момент – Уравнение действительно при При x = a Если единичная сила находится между точками А (x = 0) и С (x = а), то рассматриваем в равновесии правую часть. Тогда изгибающий момент
При x = 0 МС = 0, при x = a Следовательно, изгибающий момент График такой функции (рис 1 б) представляет собой линию влияния изгибающего момента в сечении С. Каждая ордината этого графика представляет собой численные значения изгибающего момента MC от подвижной единичной силы в тот момент, когда она находится над данной ординатой. Рассмотренный пример позволяет сделать выводы, справедливые для любой искомой величины (усилия или перемещения). Линией влияния (или инфлюентной линией) соответствующей величины называют график, выражающий закон изменения той или иной величины (например, опорной реакции, поперечной силы, изгибающего момента и т.д.), возникающей в определенном месте плоского сооружения, в функции от положения движущегося по сооружению сосредоточенного единичного груза, сохраняющего постоянное направление. Сокращенно можно писать вместо «линия влияния» - «л.в.». Каждая ордината линии влияния представляет собой численное значение рассматриваемой величины в данном сечении конструкции от единичного груза, приложенного над этой ординатой (предполагается, что линия влияния построена под расчетной схемой конструкции). Площадь, ограниченную линией влияния и осью х принято заштриховывать по направлению ординат линий влияния, делать надпись, соответствующую ее названию, и обозначать знак (см. рис. 1 б). Линия влияния вычерчивается в удобном для ее использования масштабе. Вместо указания масштаба целесообразно указывать численные значения характерных ординат (см. рис. 1 б, ордината MC при x = a). Для линий влияния, изображаемых отрезками прямых линий, этого достаточно для практического использования всей линии влияния (все остальные ординаты находятся из геометрических соображений).
|

 .
. .
. , при x = l MC = 0.
, при x = l MC = 0. . Уравнение действительно при
. Уравнение действительно при 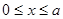 .
.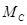 при перемещении единичной силы по балке изменяется в зависимости от положения этой силы, т.е. он является функцией положения этой силы, определяемого координатой x.
при перемещении единичной силы по балке изменяется в зависимости от положения этой силы, т.е. он является функцией положения этой силы, определяемого координатой x.


