Построение линий влияния поперечной силы
Берем проекции сил на ось z.
Уравнение равновесия левой части балки (рис. 15 а) Рис. 15
Уравнение справедливо на участке 0,1 l £ x £ l. При x = 0,1 l QА = 0,9; при x = l QA = 0. Уравнение равновесия правой части балки.
Строим линию влияния QA (рис. 14 ж). Линии влияния поперечных сил в сечениях В, С, Д и К строятся аналогично. Ординаты линий влияния Q: в сечении x = 0 ордината Q0 = 1; в сечении А (x = 0,1 l) ордината QА = 0,9; в сечении В (x = 0,2 l) ордината QВ = 0,8; в сечении С (x = 0,3 l) ордината QС = 0,7; в сечении Д (x = 0,4 l) ордината QД = 0,6; в сечении К (x = 0,5 l) ордината QК = 0,5. Определим расчетные усилия в каждом из указанных сечений с учетом того, что одна из сосредоточенных сил располагается над вершиной линий влияния (рис. 14 ж). Поперечная сила от сосредоточенных сил определяется по формуле
Тогда
Значения Q от Т приведены на рис. 14 з. Поперечная сила от действия распределенной нагрузки q в сечениях определяется по формуле:
Значения Q от q приведены на рис. 14 и. Расчетные значения поперечных сил от сосредоточенных и равномерно распределенных нагрузок определяются по формуле
QS0 = QP0 +Qq0 = 76,6 + 240 = 316,6 кН; QSА = QPА +QqА = 68,6 + 192 = 260,6 кН; QSв = QPв +Qqв = 60,6 + 144 = 204,6 кН; QSс = QPс +Qqс = 52,6 + 96 = 148,6 кН; QSд = QPд +Qqд = 44,6 + 48 = 92,6 кН; QSк = QPк +Qqк = 36,6 + 0 = 36,6 кН. Значение QS приведены на рис. 14 к. Расчетной величиной для определения касательных напряжений t в середине пролета является поперечная сила, равная 36,6 кН.
|


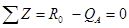 ;
; 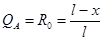 .
. . Уравнение справедливо на участке 0£ x £ 0,1 l.
. Уравнение справедливо на участке 0£ x £ 0,1 l. . При x = 0 QA = 0; при x = 0,1 l QA = -0,1.
. При x = 0 QA = 0; при x = 0,1 l QA = -0,1. . (4)
. (4) кН;
кН;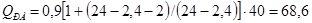 кН;
кН; кН;
кН; кН;
кН; кН;
кН;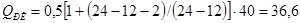 кН.
кН. . (5)
. (5) ;
; ;
; ;
;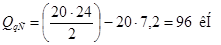 ;
; ;
; .
. . (6)
. (6)


