Вычисление румбов сторон полигона и знаков приращений у координат
1.5 Вычисление приращения координат (∆х и ∆у) выполнить, используя формулы (8-9):
где d - горизонтальное положение стороны теодолитного хода, r - румб стороны. Результаты вычислений записать в ведомость координат (табл. 6-7), округлив до 0,01м. Определить знаки приращений координат по названию румба (табл.8).
1.6.Увязка приращений координат.
Теоретическая сумма приращений координат замкнутого хода по осям Х и Y должна быть равна нулю т.е. (Σ∆хтеор= 0; Σ∆утеор= 0). Вследствие неизбежных ошибок при измерении углов и линий в полевых условиях указанные равенства не выполняются. В связи с чем появляются невязки (f∆х и f∆у) - в приращениях координат: f f Из-за присутствующих невязок fx и fy замкнутый полигон, получается разомкнутым на величину fабс, называемую абсолютной линейной ошибкой в периметре полигона, которая вычисляется по формуле (10):
Полученная величина не должна превышать значения допустимой величины линейных измерений в данных условиях. Чтобы оценить точность линейных измерений по замкнутому теодолитному ходу, следует вычислить относительную погрешность:
и сравнить с допустимой.
В разомкнутом ходе теоретическая сумма приращений координат вычисляется как разность координат точек на которые он опирается (Хк –Хн;; Ук -Ун). Невязка в разомкнутом ходе считается допустимой, если она не превышает 1/1500. При допустимости невязки, ее распределяют с обратным знаком на все приращения, пропорционально горизонтальным положениям т.е поправки в приращения вычисляют согласно формуле 12
откуда
Контролем вычисления поправок служит равенство - сумма поправок в приращения по каждой оси согласно формуле 13 должна равняться невязке с обратным знаком. Полученные поправки алгебраически прибавляют к соответствующим приращениям и получают увязанные приращения (см. соответствующие графы таблицы 7,8). Сумма увязанных приращений по каждой оси должна равняться теоретической сумме приращений.
1.7 Вычисление координат точек полигона.
После увязки приращений вычисляются координаты всех точек полигона по формулам 14
Последовательно вычисляя координаты всех точек, необходимо получить координаты исходной точки, что является контролем правильности вычислений координат всех точек полигона.
Таблица 7
|


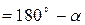


 (8)
(8) , (9)
, (9)

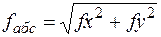 (10)
(10) (11)
(11)

 (12)
(12) (13)
(13) (14)
(14)


