Для бакалавров – заочников инженерного факультета 6 страница
2) АВ: Подставляем снова из уравнения границы у = 2 – х в заданную функцию и получим
Эта точка является граничной точкой отрезка АВ. Вычисляем 3) ОВ: у = х, Поступая аналогично, получаем:
Получили критическую точку Е (1/2,1/2), вычисляем Значения функции в граничных точках О и В мы вычисляли ранее. Итак, окончательно имеем: z(C) = 6,25; z(D) = 5,25; z(A) = 3; z(В) = 5; z(E) = 4,5. Сравнивая эти значения заключаем, что наименьшее значение z(A) = 3 достигается в граничной точке А; наибольшее значение z(C) = 6,5 достигается в точке экстремума (максимума) – точке С.
Пример 19 (к задачам 131-140). Найти вектор нормали к поверхности Решение. Уравнение нормали к поверхности S в точке
где Перепишем уравнение поверхности и найдём частные производные функции
Тогда вектор нормали к поверхности
Пример 20 (к задачам 131-140). Найти производную скалярной функции Решение. Производная скалярной функции и (x.y.z) в направлении вектора
где cos
Найдем теперь направляющие косинусы вектора
То
= а в точке М:
Найдём теперь величину и направление наибольшего изменения скалярной функции. Направление наибольшего изменения скалярной функции определяется, как градиент скалярной функции. А величина этого направления – как модуль градиента. Градиент скалярной фыункции вычислим по формуле
Для нашего примера он равен
- в произвольной точке,
- в точке М (1, -3, 4).
Тогда модуль градиента:
Пример 21. (к задачам 141-150). В указанном двойном интеграле построить область интегрирования, изменить порядок интегрирования и вычислить интеграл в обоих случаях:
Решение: Сначала построим область интегрирования D, которая разбита на две части D 1 и D 2. Область D 1 ограничена линиями (см. первое слагаемое): у = 0, у = 1, х = 0 и х = у. Область D 2 ограничена линиями (см. второе слагаемое) у = 1, у = е, х =ln у (т.е. у = ех) и х = 1. Таким образом область D, построена и заданный повторный интеграл равен двойному I= Поменяем порядок интегрирования, т.е. область D проектируем на ось Ох – она проектируется в отрезок [0,1] оси Ох. Тем самым получены нижний и верхний пределы интегрирования по переменной х. Теперь заметим, что в рамках полосы между прямыми х = 0 и х = 1 область D ограничена снизу прямой х = у или (у = х), а сверху кривой х = ln у (или у = ех) Таким образом, получаем I= Теперь вычислим интеграл в обоих случаях. I= Второй случай оказывается для вычисления более громоздким:
I= Пример 22 (к задачам 151-160). Вычислить двойной интеграл, переходя к полярным координатам: Решение: Связь между декартовыми (х, у) и полярными
J = Следовательно, Остается выяснить, как выглядит область Г с тем, чтобы знать как расставить пределы интегрирования. Можно поступать двояко. Для данного примера область D ограничена линией
- так выглядит уравнение границы области D в полярных координатах. Обычно строят границу по точкам, помня геометрический смысл полярных координат:
х 0 1
Таким образом, граница области D получилась в форме овала. Теперь из чертежа легко видеть, что угол Итак, I= Второй способ состоит в том, что область Г строим в декартовой системе координат
-
= = = = =
Пример 23 (к задачам 161-170). Выполнить действия над комплексными числами. Результаты записать в алгебраической, тригонометрической и показательной формах. Изобразить графически: а) Решение. Число j, удовлетворяющее условию Число
а) Найти частное двух комплексных чисел, записанных в алгебраической форме: Решение. Для того чтобы найти частное двух комплексных чисел в алгебраической форме, домножим числитель и знаменатель заданной дроби на число, комплексно сопряжённое знаменателю. Комплексно сопряженным числу
Мы получили результат деления в алгебраической форме: Представим число z в тригонометрической форме. Для этого вычислим, сначала, его модуль и аргумент:
Показательная:
Геометрически комплексное число
б) Вычислить Решение. Сначала запишем число
Следовательно
Тогда
- это тригонометрическая форма записи заданного комплексного числа. Сразу можем записать показательную форму:
Для того чтобы получить алгебраическую форму записи, нужно вычислить значения синуса и косинуса в тригонометерической форме:
в) Найти все значения Решение. Комплексный корень
Представим, сначале,
Отсюда получаем 4 значения корня четвертой степени из (-1):
Здесь у нас сразу записана тригонометрическая, показательная и алгебраическая формы.
Графически все полученные значения корня расположены в вершинах правильного многоугольника, вписанного в окружность радиуса  (рис. 3). (рис. 3).
|



 т.е. получили В (1,1).
т.е. получили В (1,1).


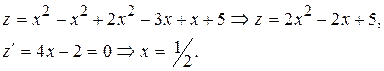

 в точке
в точке 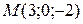 .
.  .
. имеет вид:
имеет вид: ,
,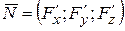 – направляющий вектор прямой нормали, то есть искомый вектор нормали;
– направляющий вектор прямой нормали, то есть искомый вектор нормали;  – уравнение поверхности S.
– уравнение поверхности S.
 в точке М:
в точке М: =
=  ,
,  =
=  ,
,
 .
. .
. в точке М (1,-3,4) в направлении вектора
в точке М (1,-3,4) в направлении вектора 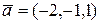 . Найти величину и направление наибольшего изменения скалярной функции в указанной точке
. Найти величину и направление наибольшего изменения скалярной функции в указанной точке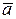 =(а 1, а 2, а 3) вычисляется по формуле:
=(а 1, а 2, а 3) вычисляется по формуле: ,
, ,cos
,cos  ,cos
,cos 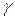 - направляющие косинусы вектора
- направляющие косинусы вектора  =
=  . В нашем примере частные производные
. В нашем примере частные производные =
=  ,
,  =
=  ,
, =
=  .
.
 =
= 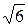 ,
, = (
= ( ,
,  ,
,  ). Следовательно, производная поля u (x,y,z) по направлению вектора
). Следовательно, производная поля u (x,y,z) по направлению вектора 
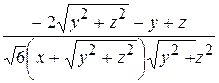 ,
,
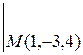 =
=  =
=  =
= 
 -0,04.
-0,04. .
.


 =
=  =
= 
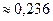 .
. I=
I=  .
.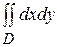 , который представляет собой площадь области D.
, который представляет собой площадь области D. =
=  =
=  =
=  = е -
= е -  - е0 = е -
- е0 = е -  .
. =
=  +
+  =
= 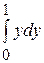 +
+  =
= 
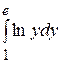 =
= 
 =
= 
 .
. координатами имеет вид:
координатами имеет вид: 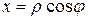 ,
,  , 0
, 0 
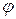 <2
<2  (или
(или  ). При этом изменяется подынтегральное выражение и область интегрирования по формуле:
). При этом изменяется подынтегральное выражение и область интегрирования по формуле: =
=  =
=  , где якобиан J вычисляется следующим образом:
, где якобиан J вычисляется следующим образом: =
=  .
. . В нашем примере f (x, y) = 1, поэтому
. В нашем примере f (x, y) = 1, поэтому 




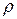 - длина радиус-вектора точки,
- длина радиус-вектора точки,  - угол, который образует этот радиус-вектор с положительным направлением оси ОХ. Поскольку всегда
- угол, который образует этот радиус-вектор с положительным направлением оси ОХ. Поскольку всегда  , то в нашем примере угол
, то в нашем примере угол  . При этом в силу четности косинуса составим табличку для построения кривой лишь для отрезка
. При этом в силу четности косинуса составим табличку для построения кривой лишь для отрезка  , а для отрезка
, а для отрезка  используем симметрию(см. рисунок).
используем симметрию(см. рисунок).



 =
= 


 y
y 




 ) до (
) до (
 .
. 1
1 
 0
0  =
=  =2
=2  =
= 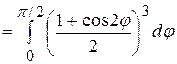 =
= 
 =
=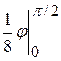
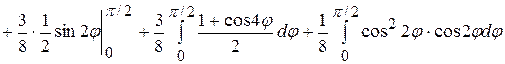 =
= =
= =
= =
=  =
= .
.
 , называется мнимой единицей. Заметим, что мнимую единицу чаще обозначают буквой i. Однако в электротехнике буквой i всегда обозначают ток, а для обозначения мнимой единицы используется j.
, называется мнимой единицей. Заметим, что мнимую единицу чаще обозначают буквой i. Однако в электротехнике буквой i всегда обозначают ток, а для обозначения мнимой единицы используется j. , где
, где 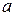 и
и  - действительные числа, представляет собой алгебраическую форму записи комплексного числа.
- действительные числа, представляет собой алгебраическую форму записи комплексного числа.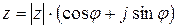 - это тригонометрическая форма записи комплексного числа. Здесь
- это тригонометрическая форма записи комплексного числа. Здесь  - модуль комплексного числа:
- модуль комплексного числа:  ; угол
; угол  .
.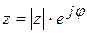 - показательная форма записи комплексного числа.
- показательная форма записи комплексного числа.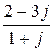 . Результат записать в алгебраической, тригонометрической и показательной формах. Изобразить графически
. Результат записать в алгебраической, тригонометрической и показательной формах. Изобразить графически . Тогда
. Тогда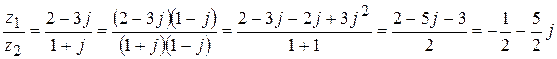 .
.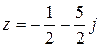 .
. ;
; рад.
рад. Тогда тригонометрическая форма записи полученного комплексного числа будет иметь вид:
Тогда тригонометрическая форма записи полученного комплексного числа будет иметь вид: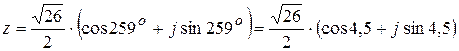 .
. .
. В нашем случае получаем изображение числа z, показанное на рис 1.
В нашем случае получаем изображение числа z, показанное на рис 1. . Результат записать в алгебраической, тригонометрической и показательной формах. Изобразить графически
. Результат записать в алгебраической, тригонометрической и показательной формах. Изобразить графически в тригонометрической форме. Для этого найдём модуль и аргумент комплексного числа.
в тригонометрической форме. Для этого найдём модуль и аргумент комплексного числа.
 . Тогда тригонометрическая форма записи комплексного числа будет
. Тогда тригонометрическая форма записи комплексного числа будет  . Для возведения полученного комплексного числа в степень n = 60 воспользуемся формулой Муавра:
. Для возведения полученного комплексного числа в степень n = 60 воспользуемся формулой Муавра:

 .
.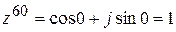 .
. - алгебраическая форма записи комплексного числа.
- алгебраическая форма записи комплексного числа. Само комплексное число
Само комплексное число  изображено на рис. 2.
изображено на рис. 2.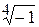 . Результат записать в алгебраической, тригонометрической и показательной формах. Изобразить графически
. Результат записать в алгебраической, тригонометрической и показательной формах. Изобразить графически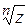 имеет п различных значений. Для того чтобы найти все эти значения, воспользуемся формулой
имеет п различных значений. Для того чтобы найти все эти значения, воспользуемся формулой .
. в тригонометрической форме:
в тригонометрической форме: , тогда
, тогда 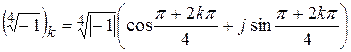 , k=0,1,2,3.
, k=0,1,2,3.







