Для бакалавров – заочников инженерного факультета 8 страница
Аналогично,
Видим, что полная вероятность Р (А) = 1/4 находится между условными вероятностями
Пример 31 (к задачам 231-240). Вероятность попадания в цель при одном выстреле равна 0,8. Составить ряд и функцию распределения числа попаданий в цель при четырех выстрелах. Вычислить математическое ожидание и дисперсию. Найти вероятность того, что при четырех выстрелах будет не менее двух попаданий. Показать графически. Решение. Во-первых, обозначим случайную величину
Проводим вычисления
Составим ряд распределения случайной величины (дискретной)
Проверяем правильность вычисления
Функцией распределения F (х) случайной величины Далее, пусть Аналогично: пусть
пусть
пусть
и, наконец, пусть х > 4, тогда:
Построим график функции F (х):
Стрелки на графике означают, что функция в точках разрыва указанного стрелкой значения не достигает. Например, Р (3)=0,1808 (но не 0,4904), а 0,4904 = F (3+0). Вычислим числовые характеристики (математическое ожидание т и дисперсию
Дисперсию Среднее квадратное отклонение Итак, мы имеем два вида закона распределения дискретной случайной величины (ДСВ) – ряд распределения и функцию распределения. Пользуясь этими законами, найдем вероятность Во-первых, эту вероятность можно расписать следующим образом:
Теперь, выбирая нужную формулу и глядя на функцию распределения, получим
Пример 32 (к задачам 241-250). Имеются данные о выходе валовой продукции (в руб.) на 1 га сельскохозяйственных угодий для 50 хозяйств;
Требуется: 1. Построить вариационный ряд частот или относительных частот; 2. Изобразить геометрически вариационный ряд, построив гистограмму частот; 3. Вычислить точечные оценки параметров распределения; 4.Высказать гипотезу о виде закона распределения признака и применить критерий согласия хи-квадрат Пирсона на 5%-м уровне значимости; 5. Считая полученный набор данных генеральной совокупностью, сделать из этой а) вычислить точечные оценки параметров распределения - выборочную среднюю арифметическую б) найти доверительный интервал для генеральной средней на уровне значимости а = 0,05 при неизвестной и известной дисперсии; в) найти доверительный интервал для генеральной дисперсии. 1) Изучается непрерывный признак X - выход валовой продукции (в руб.) на 1 га сельскохозяйственных угодий. Для непрерывного признака по результатам выборки составляется интервальный вариационный ряд. Для этого весь диапазон изменения признака X — размах вариации R = Интервальный ряд частот и относительных частот валовой продукции (руб.) на 1 га с/х угодий.
2) Графическим изображением вариационного ряда служит гистограмма частот или относительных частот. Построим гистограмму частот. Для этого на оси абсцисс откладываем отрезки, изображающие длины h интервалов изменения признака X. На этих отрезках как на основаниях строим прямоугольники с высотами, равными пi 3) Для вычисления среднего арифметического и дисперсии признака его интервальный вариационный ряд преобразуют в дискретный, заменяя каждый интервал его срединным значением. В таблице соответствующие срединные значения каждого интервала записаны в первой строке таблицы. Теперь можно заняться вычислением числовых характеристик. Они вычисляются так же, как для дискретных рядов. Выборочная средняя арифметическая:
Выборочная дисперсия:
Выборочное среднее квадратическое отклонение: Коэффициент вариации: Каждое из полученных значений числовых характеристик задаются одним числом (т.е. одной точкой на числовой прямой), поэтому они называются точечными оценками неизвестных параметров всей генеральной совокупности. Всякое высказывание о генеральной совокупности, проверяемое по выборке, называется статистической гипотезой. Статистические гипотезы классифицируют на гипотезы о законах распределения и гипотезы о параметрах распределения. Критерии проверки статистических гипотез о законе распределения называются критериями согласия. Критерий согласия хи-квадрат Пирсона — самый старый и самый распространенный. 4) Пусть в результате п наблюдений признака X получен вариационный ряд. Анализ выборки (например, по виду гистограммы частот - если в нашем примере через верхние основания прямоугольников гистограммы провести плавную линию, то она будет иметь колоколообразную форму, т.е. похожа на график плотности вероятности нормального распределения) приводит нас к предположению о некотором (например, нормальном) законе распределения признака X. Параметры этого распределения, если заранее не известны, оцениваются по выборочным данным и, таким образом, нам становится известным предполагаемый теоретический закон распределения. По этому закону легко определить вероятности
которая оказывается распределенной по закону хи-квадрат. Как уже говорилось, есть основание предполагать, что признак X в нашем примере распределен по нормальному закону. Итак, мы высказываем гипотезу о том, что признак X распределен по нормальному закону с математическим ожиданием Теоретические частоты
Отметим, что для вычисления вероятностей по этой формуле левый конец первого интервала следует брать равным ( р1=Ф = Ф ( р2=Ф = 0,0478+0,2642 = 0,312; Продолжая аналогичные вычисления для остальных интервалов, найдем вероятности и соответствующие им теоретические частоты. Результаты вычислений приведены в следующей таблице.
Интервальный вариационный ряд фактических и теоретических частот и относительных частот выхода валовой продукции (руб.) на 1 га сельскохозяйственных угодий
Теперь вновь построим гистограмму частот и на этом рисунке по результатам проведенных вычислений построим график теоретического нормального распределения, т.е. наряду с фактическими частотами построим и теоретические.
В нашем примере объединим последние три интервала. В результате получим 4 интервала (т = 4):
Применяем формулу критерия хи-квадрат, учитывая, что число к степеней свободы критерия
Таким образом, получили фактическое значение критерия Следует заметить, что если бы критерий хи-квадрат Пирсона (или какой-нибудь другой) дал положительный результат ( 5) В этом пункте, собственно, демонстрируется выборочный метод. При изучении признака, характеризующего некоторую совокупность однородных объектов, не всегда имеется возможность обследовать каждый объект изучаемой совокупности. Например, для выяснения среднего срока службы электрических лампочек, изготовляемых некоторым заводом, абсурдно проверять продолжительность горения каждой лампочки. Для выяснения некоторых качественных показателей всей совокупности (она называется генеральной совокупностью) исследованию подвергают лишь небольшую часть её, отобранную случайно. Эта часть называется выборочной совокупностью (или просто выборкой). Задача математической статистики состоит в изучении методов, позволяющих делать научно обоснованные выводы о характеристиках признака X генеральной совокупности по исследованию выборки из неё. Основным условием, которое предъявляется к выборке, для того, чтобы она наиболее достоверно отражала все существенные особенности генеральной совокупности, является случайность отбора. В зависимости от способа отбора различают выборки следующих типов: собственно случайные повторные, собственно случайные бесповторные, механические, типические, серийные и т.д. Обозначим математическое ожидание и дисперсию признака X соответственно через а и
Каждая из оценок
|

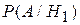 – вероятность события А при условии, что событие (гипотеза)
– вероятность события А при условии, что событие (гипотеза)  произошло, т.е. вероятность появиться шестерке, если выбран правильный кубик, равна
произошло, т.е. вероятность появиться шестерке, если выбран правильный кубик, равна  :
:  =
=  Поэтому
Поэтому
 =(число попаданий в цель при четырех выстрелах). Очевидно, СВ
=(число попаданий в цель при четырех выстрелах). Очевидно, СВ  , где
, где  - вероятность того, что в результате опытов событие (в нашей задаче – попадание в цель) появится равно т раз, р - вероятность события в одном опыте (в нашей задаче р= 0,8), q – вероятность противоположного события;
- вероятность того, что в результате опытов событие (в нашей задаче – попадание в цель) появится равно т раз, р - вероятность события в одном опыте (в нашей задаче р= 0,8), q – вероятность противоположного события; =
=  , 0! = 1.
, 0! = 1. ;
;  ;
; ;
; 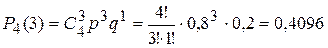 ;
; .
.
 , т.е. вероятность того, что СВ
, т.е. вероятность того, что СВ  . Для дискретных СВ функция распределения является дискретной (т.е. разрывной) разрывы функция терпит в точках хi. Действительно проводим вычисления для нашей задачи: если
. Для дискретных СВ функция распределения является дискретной (т.е. разрывной) разрывы функция терпит в точках хi. Действительно проводим вычисления для нашей задачи: если  , то событие (
, то событие ( ) – невозможное Æ и, следовательно,
) – невозможное Æ и, следовательно,  Р (Æ) = 0.
Р (Æ) = 0. . Тогда
. Тогда  .
. , тогда:
, тогда:
 , тогда:
, тогда: ;
;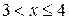 , тогда:
, тогда: ;
;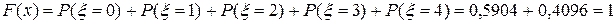 .
. F (х):
F (х):

 1
1
 0,4904
0,4904 0,1808
0,1808
 0,0016
0,0016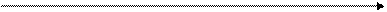 0 1 2 3 4 х
0 1 2 3 4 х ):
): .
. , или по формуле
, или по формуле  . По последней формуле имеем
. По последней формуле имеем  .
. = 0,7936.
= 0,7936.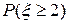 .
. и, глядя на ряд распределения, получаем, что
и, глядя на ряд распределения, получаем, что 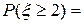 0,1536 + 0,4096 + 0,4096 = 0,9728. Этот же результат можно получить, используя функцию распределения по формулам:
0,1536 + 0,4096 + 0,4096 = 0,9728. Этот же результат можно получить, используя функцию распределения по формулам: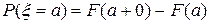 ;
;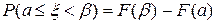 ;
; ;
; ;
;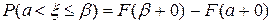 .
. 0,9728.
0,9728. (10) и исправленную выборочную дисперсию
(10) и исправленную выборочную дисперсию  (10), сравнить полученные значения с соответствующими характеристиками генеральной совокупности;
(10), сравнить полученные значения с соответствующими характеристиками генеральной совокупности; , разобьем на несколько интервалов длины h. Обычно рекомендуется разбивать на 5-10 интервалов одинаковой длины. Вообще, для выбора такой длины h интервала, чтобы ряд распределения не был слишком громоздким и в то же время отражал характерные черты распределения, рекомендуется использовать формулу Стэрджеса:
, разобьем на несколько интервалов длины h. Обычно рекомендуется разбивать на 5-10 интервалов одинаковой длины. Вообще, для выбора такой длины h интервала, чтобы ряд распределения не был слишком громоздким и в то же время отражал характерные черты распределения, рекомендуется использовать формулу Стэрджеса:  . При этом за правый конец первого интервала следует взять (
. При этом за правый конец первого интервала следует взять ( ), а за левый конец последнего — (
), а за левый конец последнего — ( ). В нашей задаче R=1081-250=831 и по формуле Стэрджеса получаем
). В нашей задаче R=1081-250=831 и по формуле Стэрджеса получаем  . Обычно значение h, вычисленное по формуле Стэрджеса, округляют до удобного для вычислений значения. Возьмем h = 150, а за правый конец первого интервала —
. Обычно значение h, вычисленное по формуле Стэрджеса, округляют до удобного для вычислений значения. Возьмем h = 150, а за правый конец первого интервала —  . Итак, получаем интервальный ряд частот и относительных частот.
. Итак, получаем интервальный ряд частот и относительных частот.


 ;
; (39,5%).
(39,5%). того, что признак примет значение, принадлежащее i -му интервалу. Отсюда для выборки объема n получаем теоретические частоты
того, что признак примет значение, принадлежащее i -му интервалу. Отсюда для выборки объема n получаем теоретические частоты  и сравниваем их с фактическими
и сравниваем их с фактическими  . В качестве меры расхождения теоретического и эмпирического ряда частот берется случайная величина
. В качестве меры расхождения теоретического и эмпирического ряда частот берется случайная величина  (читается как хи-квадрат):
(читается как хи-квадрат): =
=  ,
, и средним квадратическим отклонением
и средним квадратическим отклонением  (или дисперсией
(или дисперсией  2=32184).
2=32184). находятся по формуле
находятся по формуле 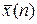 и дисперсией
и дисперсией  , то вероятность
, то вероятность 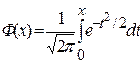 по формуле
по формуле .
. ), а правый конец последнего интервала равным (
), а правый конец последнего интервала равным ( ). Значения функции Лапласа берем из таблицы. В условиях нашей задачи получаем:
). Значения функции Лапласа берем из таблицы. В условиях нашей задачи получаем: Ф
Ф  =Ф (–0,72) – Ф (
=Ф (–0,72) – Ф (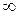 ) =
) = 0,2358=11,79.
0,2358=11,79. – Ф
– Ф  = Ф (–0,12) – Ф (–0,72) = Ф (0,12) + Ф (0,72) =
= Ф (–0,12) – Ф (–0,72) = Ф (0,12) + Ф (0,72) = 15,6.
15,6.
 На рисунке получившаяся ступенчатая фигура заштрихована. Отчетливо видны расхождения между эмпирическим (выборочным) и теоретическим распределениями. Остается выяснить существенно ли на заданном уровне значимости а = 0,05 это расхождение. Ответ на этот вопрос и дает случайная величина
На рисунке получившаяся ступенчатая фигура заштрихована. Отчетливо видны расхождения между эмпирическим (выборочным) и теоретическим распределениями. Остается выяснить существенно ли на заданном уровне значимости а = 0,05 это расхождение. Ответ на этот вопрос и дает случайная величина  . Число k степеней свободы этой случайной величины определяется соотношением k = т – 3, где т – число различных интервалов в вариационном ряду. Необходимо учесть следующее замечание: малочисленные частоты (
. Число k степеней свободы этой случайной величины определяется соотношением k = т – 3, где т – число различных интервалов в вариационном ряду. Необходимо учесть следующее замечание: малочисленные частоты ( ) следует объединить. В этом случае ответствующие им теоретические частоты также надо сложить, а при определении числа степеней свободы по формуле k = т – 3 в качестве т принять число групп выборки, оставшихся после объединения частот.
) следует объединить. В этом случае ответствующие им теоретические частоты также надо сложить, а при определении числа степеней свободы по формуле k = т – 3 в качестве т принять число групп выборки, оставшихся после объединения частот.

 = 6,73. По табл. распределения
= 6,73. По табл. распределения  = 3,8. Итак, получаем, что фактическое значение критерия превысило критическое (6,73 > 3,8), поэтому на уровне значимости а = 0,05 гипотезу о том, что признак X распределен по нормальному закону, следует отвергнуть.
= 3,8. Итак, получаем, что фактическое значение критерия превысило критическое (6,73 > 3,8), поэтому на уровне значимости а = 0,05 гипотезу о том, что признак X распределен по нормальному закону, следует отвергнуть. естественно, будут меняться от выборки к выборке. Таким образом, каждое значение
естественно, будут меняться от выборки к выборке. Таким образом, каждое значение  считается не числом, а случайной величиной
считается не числом, а случайной величиной 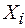 , имеющей те же числовые характеристики а и
, имеющей те же числовые характеристики а и  результатовнаблюдения, с помощью которой судят о значении параметра
результатовнаблюдения, с помощью которой судят о значении параметра 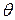 называется оценкой (или статистикой) параметра
называется оценкой (или статистикой) параметра  .
.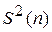 определяется одним числом, т.е. точкой на числовой прямой, и потому называются точечными оценками. Необходимо, однако, всегда помнить, что нахождение точечной оценки некоторого параметра - это лишь первый этап. Далее обязательно надо найти точность этой оценки или, как говорят, доверительный интервал. Интервал (
определяется одним числом, т.е. точкой на числовой прямой, и потому называются точечными оценками. Необходимо, однако, всегда помнить, что нахождение точечной оценки некоторого параметра - это лишь первый этап. Далее обязательно надо найти точность этой оценки или, как говорят, доверительный интервал. Интервал (  1<
1< 


