Для бакалавров – заочников инженерного факультета 9 страница
Вероятность р = 1 – α называется доверительной вероятностью или надежностью оценки и задается близкой к единице, обычно 0,9; 0,95 или 0,99. Число α; называется уровнем значимости. Границы доверительного интервала находятся с помощью статистик, которые являются случайными величинами. Следовательно, случайны и границы интервала. Поэтому, говорят, что доверительный интервал накроет неизвестный параметр В нашей задаче требуется найти доверительный интервал для неизвестного значения генеральной средней с надежностью 0,95. Как уже говорилось, оценкой генеральной средней является выборочная средняя
Значения функции Лапласа Преобразуем это неравенство:
откуда получаем доверительный интервал Р ( Отметим, что в эти формулы входит Предположим сначала, что генеральная дисперсия нам известна и равна а) Выборка объема 10 включает следующие значения признака X: 535, 278,312, 368, 327, 482, 318, 531, 554,898. Для этой малой выборки найдем выборочные числовые характеристики.
= 243193,5 =>
S 2(10) = 243193,5 – 211876,1 = 31317,4,
Итак, выборочная средняя арифметическая б) Итак, найдем по выше приведенным формулам доверительный интервал для неизвестного матожидания а при известной дисперсии
Подставляем значения:
или 349,1 < a < 571,5. Итак, доверительный интервал (349,1; 571,5) с надежностью 95% накроет неизвестное математическое ожидание а. Заметим, что истинное математическое ожидание а = 454 оказалось внутри доверительного интервала. В действительности на практике чаще всего генеральная дисперсия В этом случае воспользуемся следующей теоремой: пусть Х1,Х2,...,Хп - независимые случайные величины, распределенные одинаково по нормальному закону с математическим ожиданием а и дисперсией Доверительный интервал с помощью этой теоремы строится следующим образом. Пусть признак X распределен нормально с математическим ожиданием (генеральной средней) а и дисперсией (генеральной дисперсией) Р ( Расписав это условие подробнее, получим формулу для определения искомого доверительного интервала: Р ( Р ( Таким образом, с вероятностью р можно утверждать, что доверительный интервал Подставим в окончательную формулу данные нашедшего примера:
т.е. 326,9 < а < 593,7. Итак, теперь мы утверждаем более слабое предложение: с надежностью 95% (или с вероятностью 0,95) интервал (326,9; 593,7) накроет неизвестное математическое ожидание а (генеральную среднюю). Утверждение это действительно более слабое, т.к. доверительный интервал оказался шире, т.е. оценка оказалась грубее. Это естественная плата за потерю информации о генеральной дисперсии. в) Для нахождения доверительного интервала для неизвестной дисперсии
Учитывая, что число степеней свободы k = п –1= 9, находим по указанным таблицам
Заметим, что истинное значение генеральной дисперсии
Пример №33 (к задачам 251-260). Втаблице приведены данные опыта по изучению действия соотношения N:Р2O5:К2О при питании рассады томатов на урожай плодов (ц/га). Каждое соотношение испытывалось на четырех участках. Методом дисперсионного анализа изучить влияние соотношения на урожайность плодов. Установить существенность влияния фактора при уровне значимости 0,05. Урожайность плодов томатов в зависимости от соотношения N:Р2O5:К2О при питании рассады.
Решение. Задачей дисперсионного анализа является изучение влияния одного или нескольких факторов на рассматриваемый признак. Факторами обычно называют внешние условия, влияющие на эксперимент. Если изучают влияние одного фактора F на результирующий признак X, то имеет место однофакторный анализ, которым нам необходимо научиться пользоваться. В условиях эксперимента фактор F может принимать различные значения, изменяться, или, как говорят, может варьировать на разных уровнях F1,F2,...., FР. Например, если требуется выяснить влияние удобрений на урожайность, то здесь результирующий признак X - урожайность, фактор F - удобрение, а уровни F1,F2,...., FР фактора - виды удобрений. Для большей достоверности на практике проводятся несколько испытаний, т.е. как говорят, осуществляют повторности. Будем предполагать, что число наблюдений для каждого уровня одинаково и равно п. Тогда результаты наблюдений можно свести в таблицу.
Исходные данные дисперсионного анализа.
Введем обозначения:
т.е. Мы уже видели, что мерой вариации признака является сумма квадратов отклонений значений признака от средней. Можно доказать следующий результат: Сумма Q называется полной суммой квадратов отклонений. Отдельных наблюдений от общей средней. Слагаемое Q1 называется рассеиванием по факторам, оно характеризует отклонение средних для факторных уровней от общей средней. Слагаемое Q2 называется остаточным рассеиванием и характеризует расхождение между наблюдениями i-ro уровня, т.е. за счет неучтенных факторов. Таким образом, формула показывает, что общее рассеивание значений признака X, измеряемое суммой Q, складывается из двух компонент Q1 и Q2, характеризующих рассеивание под влиянием фактора F (Q1) и остаточное рассеивание (Q2) под влиянием неучтенных факторов. С помощью Q, Q1, Q2 производится оценка общей, межгрупповой и внутригрупповой дисперсией:
Сравнивая дисперсию по факторам Сравнение осуществляется с помощью отношения F(k1,k2) = Теперь обратимся к нашему примеру. В нашей задаче р = 5, п = 4, рп = 20. Вычисляем среднюю арифметическую по каждому уровню фактора F.
Общую среднюю
При вычислении факторной Q1=п· Подставляя данные задачи в формулы, получим:
п· пр(
Теперь находим фактическое значение Fфакт критерия Fпо формуле для F(k1,k2). В заключение приведем некоторые извлечения из таблиц распределения Фишера-Снедекора, которые потребуются при выполнении контрольных работ.
Пример 34 (к задачам 261-270). Имеются статистические данные по группе предприятий о зависимости годовой производительности труда Y в расчете на одного рабочего (тыс. руб.) от энерговооруженности X (квт.ч. на одного рабочего) на 10 предприятиях одной отрасли:
Методом корреляционного анализа исследовать зависимость между этими признаками. Рассчитать коэффициенты регрессии и корреляции. Построить график корреляционной зависимости.
Решение. Построим диаграмму рассеивания. Для этого на оси абсцисс откладываем значения хi, факторного признака X, а на оси ординат - соответствующие значения yi результирующего признака Y. Получающиеся таким образом точки с координатами (хi;yi) образуют диаграмму рассеивания (см. рисунок) .
Визуальные наблюдения позволяют высказать предположение о наличии линейном корреляционной зависимости, поскольку точки диаграммы рассеивания (иначе она называется корреляционным полем) как бы выстраиваются вдоль некоторой прямой линии. Итак, предполагаем, что между энерговооруженностью X (квт.ч. на 1 рабочего) и годовой производительностью труда Y (тыс. руб. на 1 рабочего) существует линейная корреляционная зависимость. Соответствующее уравнение прямой линии называется уравнением прямой регрессии Y на X и имеет вид:
где коэффициент регрессии
Выборочный коэффициент корреляции r определяется по формуле:
|

 с доверительной вероятностью р.
с доверительной вероятностью р.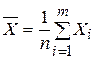 , которая, в соответствии с ГИВД, рассматривается как сумма независимых и одинаково распределенных случайных величин
, которая, в соответствии с ГИВД, рассматривается как сумма независимых и одинаково распределенных случайных величин  . Если признак X распределен нормально с математическим ожиданием а и дисперсией
. Если признак X распределен нормально с математическим ожиданием а и дисперсией  , то доказано, что случайная величина
, то доказано, что случайная величина  распределена тоже по нормальному закону - c тем же математическим ожиданием а и дисперсией
распределена тоже по нормальному закону - c тем же математическим ожиданием а и дисперсией  . Тогда случайная величина
. Тогда случайная величина  распределена нормально с нулевым математическим ожиданием и дисперсией, равной единице, следовательно, вероятность того, что значения этой случайной величины по абсолютной величине не превзойдут числа ZР, вычисляется по формуле
распределена нормально с нулевым математическим ожиданием и дисперсией, равной единице, следовательно, вероятность того, что значения этой случайной величины по абсолютной величине не превзойдут числа ZР, вычисляется по формуле
 находятся из таблиц. По условию задачи задана вероятность р = 0,95, следовательно, число находится из условия
находятся из таблиц. По условию задачи задана вероятность р = 0,95, следовательно, число находится из условия  ,
,  , значение
, значение  находим по таблицам. Итак, с вероятностью р = 0,95 можно утверждать, что выполняется неравенство
находим по таблицам. Итак, с вероятностью р = 0,95 можно утверждать, что выполняется неравенство  .
.
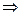
 <a<
<a<  ,
, для неизвестного параметра а, следовательно, исходное условие можно переписать в виде:
для неизвестного параметра а, следовательно, исходное условие можно переписать в виде: <a<
<a<  )=
)= 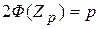 .
. , следовательно, ими можно пользоваться лишь в случае, когда генеральная дисперсия известна (что на практике бывает не всегда).
, следовательно, ими можно пользоваться лишь в случае, когда генеральная дисперсия известна (что на практике бывает не всегда). = 32184, а
= 32184, а  (10) =
(10) =  (535 + 278 + 312 + 368 + 327 + 482 + 3 18 + 53 1 + 554 + 898) = 460,3;
(535 + 278 + 312 + 368 + 327 + 482 + 3 18 + 53 1 + 554 + 898) = 460,3; ;
; =
=  (5352 +2782 +3122 +3682 +3272 + 4822 +3182 +5312 +5542 +8982)=
(5352 +2782 +3122 +3682 +3272 + 4822 +3182 +5312 +5542 +8982)= ;
;  = 186,5
= 186,5 исправленное выборочное среднее квадратическое отклонение
исправленное выборочное среднее квадратическое отклонение  =32184,
=32184, 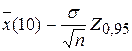 <a<
<a<  ,
, <a<
<a<  ,
, имеет распределение Стьюдента с п – 1 степенями свободы.
имеет распределение Стьюдента с п – 1 степенями свободы. интервала, для которого выполняется следующее условие:
интервала, для которого выполняется следующее условие: <
<  <
<  )=
)= 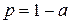 .
. <
<  < а <
< а <  ) = р.
) = р. накроет неизвестную генеральную среднюю а.
накроет неизвестную генеральную среднюю а. = 0,95;
= 0,95;  = 2,262 (найдено по таблицам распределения Стьюдента). Получим
= 2,262 (найдено по таблицам распределения Стьюдента). Получим < а <
< а < 
 , где
, где  и
и  находят по таблицам распределения
находят по таблицам распределения  из условий:
из условий: и
и  .
.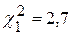 ;
;  и получаем доверительный интервал для неизвестной генеральной дисперсии
и получаем доверительный интервал для неизвестной генеральной дисперсии .
. оказалось внутри доверительного интервала.
оказалось внутри доверительного интервала.
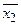

 =
= 
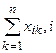 =1,2,…,р;
=1,2,…,р;  =
= 
 =
= 
 ,
, - общая средняя арифметическая всех р · п наблюдений.
- общая средняя арифметическая всех р · п наблюдений. = п·
= п· 
 , т.е. Q=Q1+ Q2.
, т.е. Q=Q1+ Q2.
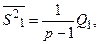

 с остаточной дисперсией
с остаточной дисперсией  , по величине их отношения судят, насколько рельефно проявляется влияние фактора - в этом сравнении и заключается основная идея дисперсионного анализа.
, по величине их отношения судят, насколько рельефно проявляется влияние фактора - в этом сравнении и заключается основная идея дисперсионного анализа. /
/  ,которое является случайной величиной, имеющей F - распределение Фишера с k1 = р - 1, k2 = р(n-1) степенями свободы. Критическое значение критерия на заданном уровне значимости находят по таблицам.
,которое является случайной величиной, имеющей F - распределение Фишера с k1 = р - 1, k2 = р(n-1) степенями свободы. Критическое значение критерия на заданном уровне значимости находят по таблицам. (454 + 470 + 430 + 500) = 463,5;
(454 + 470 + 430 + 500) = 463,5;  = 607;
= 607;  =424;
=424;  = 440.
= 440. (463,5+ 512,25 + 607 + 424 + 440) = 489,35.
(463,5+ 512,25 + 607 + 424 + 440) = 489,35. -пр(
-пр( -п
-п 
 ,
, ,
, ;
;  ;
; =
=  ;
;  =
=  ;
; 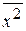 =
=  ;
;  .
.


