Для бакалавров – заочников инженерного факультета 2 страница
70.
Тема №5. Приложения дифференциального исчисления.
В задачах 71-80 провести полное исследование функции и построить её график. 71. 75. 78.
Средствами дифференциального исчисления решить задачи 81-90 (задачи на экстремум).
81. Через точку А(3,5) провести прямую с отрицательным угловым коэффициентом так, чтобы площадь треугольника, образованного ею с осями координат была наименьшей. 82. Дан равнобедренный треугольник АВС с основанием АС=а и углом при основании 83. Нужно построить здание с площадью основания 96м2. Известно, что метр стены по фасаду будет стоить в два раза дороже метра других стен. Каковы должны быть размеры здания, чтобы стоимость возведения стен была наименьшей? 84. Два самолета летят в одной плоскости и прямолинейно под углом 120 0 с одинаковой скоростью V км/час. В некоторый момент один самолет пришел в точку пересечения линий движения, а второй не дошел до неё а км. Через сколько времени расстояние между самолетами будет наименьшим и чему равно это расстояние? 85. Завод Д нужно соединить шоссейной дорогой с прямолинейной железной дорогой, на которой расположен город А. Расстояние ДВ до железной дороги равно а, расстояние АВ по железной дороге равно ℓ. Стоимость перевозок по шоссе в m раз дороже (m>1) стоимости перевозок по железной дороге. Как провести шоссе ДР к железной дороге, чтобы стоимость перевозок от завода к городу была наименьшей? 86. Для выполнения сельскохозяйственных работ трактору необходимо переехать с поля А на другое В, предварительно пополнив запасы горючего на шоссе. Расстояние АМ от поля до шоссе равно 2 км. Расстояние ВN от поля В до шоссе равно 1,5 км. Шоссе прямолинейное, МN=3,5км. В каком месте шоссе должен ожидать бензовоз, чтобы путь трактора от поля А до поля В был наименьшим? 87. Испытания двигателя привели к n различным значениям х1, х2,….,хn исследуемой величины А. Обычно в качестве значения неизвестной величины А принимают такое значение х, при котором сумма квадратов его отклонений от х1, х2,….,хn имеет наименьшее значение. Найти х, удовлетворяющее этому требованию. 88. Известно, что прочность балки с прямоугольным поперечным сечением прямо пропорциональна ширине и квадрату толщины. Найти ширину бруска наибольшей прочности, который можно вырезать из бревна диаметром 16 см. 89. Цена бриллианта пропорциональна квадрату его веса. Исследовать, как изменится стоимость бриллианта, если его разрезать на две части. Сделать обобщающий вывод для n частей. 90. От канала шириной 4м под прямым углом к нему отходит другой канал шириной 2м. Какой может быть длина бревна, чтобы его можно было сплавить по этим каналам из одного в другой (толщину бревна не учитывать).
Тема №6. Неопределенный интеграл. В задачах 91-100 требуется найти неопределенные интегралы. Результат первого интегрирования проверить дифференцированием.
91.
92.
93.
94.
95.
96. 97.
98.
99.
100.
Тема №7. Определенный интеграл.
В задачах 101-110 вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
101. 103. 105. 107. 109.
Контрольная работа №2. Тема №8. Функции нескольких переменных (ФНП). В задачах 111-120 число А вычислить приближенно с помощью дифференциала функции двух переменных.
111. 113. 115.
117.
119.
В задачах 121-130 найти наибольшее и наименьшее значения функции двух переменных в замкнутой области D, ограниченной указанными линиями. Сделать чертеж. 121. 122. 123. 124. 125. 126. 127. 128. 129. 130.
В задачах 131-140 найти производную скалярной функции
131. 132. 133. 134. 135. 136. 137. 138. 139. 140.
Тема №9. Кратные интегралы. В задачах 141-150 требуется построить область интегрирования, изменить порядок интегрирования и вычислить интегралы в обоих случаях. 141. 143. 145. 147. 149.
В задачах 151-160 требуется вычислить двойные интегралы по области D, ограниченной указанными линиями, переходя к полярным координатам.
151. 152. 153. 154. 155. 156. 157. 158. 159. 160.
Тема №10. Комплексные числа. В задачах 161-170 требуется выполнить действия над комплексными числами. Результаты записать в алгебраической, тригонометрической и показательной формах. Изобразить геометрически. 161. 162. 163.
164.
165. 166. 167.
168.
169. 170.
Тема №11 Обыкновенные дифференциальные уравнения (ДУ). В задачах 171-180 найти общие решения указанных дифференциальных уравнений (ДУ). Последнее ДУ решить двумя способами – методом вариации произвольных постоянных и методом неопределенных коэффициентов (по виду правой части). Для первого ДУ найти интегральную кривую, проходящую через точку (1;1). 171. 172. 173. 174. 175. 176. 177. 178. 179. 180. Контрольная работа №3.
Тема №12. Числовые и степенные ряды. В задачах 181-190 найти интервал сходимости степенного ряда и исследовать сходимость на границах интервала.
В задачах 191-200 вычислить с точностью до 0,001 определенный интеграл разложением подынтегральной функции в ряд Маклорена.
Тема №13. Теория вероятностей. 201. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,7; для второго и третьего стрелков эти вероятности соответственно равны 0,8 и 0,9. Найти вероятность того, что:1) только один из стрелков поразит цель; 2) только два стрелка поразят цель; 3) все три стрелка поразят цель. 202. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8; для второго и третьего орудия эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что: 1) только один снаряд поразит цель; 2) только два снаряда поразят цель; 3) все три снаряда поразят цель. 203. Два стрелка произвели по одному выстрелу по мишени. Вероятность поражения мишени каждым из стрелков равна 0,9. Найти вероятность того, что: 1) оба стрелка поразят мишень; 2) оба стрелка промахнутся; 3) только один стрелок поразит мишень; 4) хотя бы один из стрелков поразит мишень. 204. От аэровокзала отправились 2 автобуса – экспресса к трапам самолетов. Вероятность своевременного прибытия каждого автобуса в аэропорт равна 0,95. Найти вероятность того, что: 1) оба автобуса придут вовремя; 2) оба автобуса опоздают; 3) только один автобус прибудет вовремя; 4) хотя бы один автобус прибудет вовремя. 205. На участке две бригады. Вероятность выполнения плана первой бригадой равна 0,8; а вероятность выполнения плана второй 0,9. Требуется найти: 1) вероятность выполнения плана участком; 2) вероятность выполнения плана только одной бригадой участка; 3) вероятность выполнения плана хотя бы одной бригадой участка. 206. Экзаменационный билет содержит три вопроса. Вероятность того, что студент даст правильный ответ на первый вопрос равна 0,9; вероятность правильного ответа на второй вопрос равна 0,8; на третий вопрос равна 0,7. Найти вероятность того, что студент ответит: 1) на все три вопроса правильно; 2) хотя бы на два вопроса. 207. Передающее устройство, канал связи и принимающее устройство могут быть повреждены. Вероятности повреждения соответственно равны 0,5; 0,4; 0,6. Найти вероятность того, что: 1) будет повреждено хотя бы одно; 2) хотя бы одно не будет повреждено; 3) система будет работать. 208. Коэффициенты использования рабочего времени у двух комбайнов соответственно равны 0,8 и 0,6. Считая, что остановки в работе каждого комбайна возникают случайно и независимо друг от друга, определить относительное время: 1) совместной работы комбайнов; 2) работы только одного комбайна; 3) простоя обоих комбайнов. 209. Рабочий обслуживает три станка. Известно, что вероятность бесперебойной работы на протяжении одного часа после наладки равна для первого станка 0,9; для второго станка 0,8 и для третьего станка 0,7. Найти вероятность того, что за этот час: 1) лишь один станок откажет в работе и потребует вмешательства рабочего; 2) два станка потребуют вмешательства рабочего; 3) ни один станок не потребует вмешательства рабочего. 210. На ферме две бригады. Вероятность выполнения плана первой бригадой 0,7; второй 0,8. Найти вероятность: 1) выполнения плана фермой; 2) выполнение плана только одной бригадой; 3) выполнения плана хотя бы одной бригадой? 211. В группе 6 отличников, 10 хорошистов и 9 троечников. На экзамене отличники могут получить оценку «4» с вероятностью 0,3; хорошисты с вероятностью 0,8; троечники – с вероятностью 0,2. Найти вероятность того, что студент, вызванный первым, получит оценку «4». 212. При проверке качества зерен пшеницы было установлено, что все зерна могут быть разделены на 4 группы. К зернам 1-й группы принадлежит 96%, ко второй 2%, к 3-й 1%, к 4-й 1% всех зерен. Вероятность того, что из зерна вырастет колос, содержащий не менее 50 зерен для 1-й группы равна 0,5; 2-й группы 0,2; 3-й группы 0,18; 4-й группы 0,02. Найти вероятность того, что из взятого наугад зерна вырастет колос, содержащий не менее 50 зерен. 213. Брак в продукции завода вследствие дефекта А составляет 5%, причем среди забракованной продукции по признаку А в 10% случае встречается дефект В, а в продукции свободной от дефекта А, дефект В встречается в 1% случаев. Найти вероятность того, что дефект В не встретится во всей продукции. 214. Изделие проверяется на стандарт одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу равно 0,55; а ко второму 0,45. Вероятность того, что стандартное изделие будет принято первым товароведом равно 0,9; а вторым 0,98. Найти вероятность того, что наудачу взятое изделие будет признано стандартным. 215. На сборку поступают детали с 2-х автоматов. Первый дает в среднем 0,2% брака, второй 0,1%. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 2000 деталей, а со второго – 3000. 216. Из урны, содержащей 3 белых и 2 черных шара, переложено 2 шара в урну, содержащую 4 белых и 4 черных шара. Найти вероятность вынуть после этого из второй урны белый шар. 217. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых автомашин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъезжает машина. Найти вероятность того, что машина будет заправляться. 218. В вычислительной лаборатории имеются 6 новых и 4 старых машин. Вероятность того, что за выполнение некоторого расчета новая машина не выдаст ошибку равна 0,95; для старой машины эта вероятность равна 0,8. Студент проводит расчет на удачу выбранной машине. Найти вероятность того, что машина не выдаст ошибку. 219. Исследование больного вызвало предположение о возможности одного из 3-х заболеваний А1 А2 А3 с вероятностями: Р(А1)=5/12; Р(А2)=1/3; Р(А3)=1/4. Для уточнения диагноза был произведен некоторый анализ, который при первом заболевании дает положительный ответ с вероятностью 0,8; при втором – с вероятностью 3/8; при третьем – с вероятностью 1/6. Какова вероятность точного ответа. 220. В партии 600 лампочек: 200 штук изготовлены на 1-м заводе, 250 – на 2-м; 150 – на 3-м. Вероятность того, что лампочка окажется стандартной для 1-го завода, равна 0,97; для второго 0,91; для третьего 0,93. Какова вероятность того, что наудачу взятая лампочка окажется стандартной. 221. Устройство состоит из 3-х независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить ряд и функцию распределения числа отказавших элементов в одном опыте. Найти математическое ожидание и дисперсию. Вычислить вероятность того, что откажут не менее двух элементов. Проиллюстрировать геометрически. 222. В партии из шести деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составить ряд и функцию распределения числа стандартных деталей среди отобранных. Найти числовые характеристики. Вычислить вероятность того, что число стандартных деталей не меньше двух. 223. Выпущено 1000 билетов лотереи, причем разыгрываются: один выигрыш в 50 руб., 5 выигрышей по 25 руб., 10 выигрышей по 10 руб., 25 выигрышей по 5 руб. Составить ряд и функцию распределения стоимости выигрыша для владельца одного билета. Найти «справедливую» цену одного билета. 224. На поле 5 тракторов. Надежность (т.е. вероятность безотказной работы) каждого равна 0,8. Составить ряд и функцию распределения числа тракторов, работающих одновременно. Найти среднее число исправных тракторов. Вычислить вероятность того, что исправных тракторов больше 3. Показать графически. 225. В связке имеется 5 различных ключей, из которых только одним можно открыть дверь. Наудачу выбирается ключ и делается попытка открыть им дверь. Ключ, оказавшийся неподходящим больше не используется. Построить ряд и функцию распределения числа использованных ключей. Найти вероятность того, что: а) дверь будет открыта вторым ключом; б) будет использовано не меньше двух ключей. Показать графически. 226. Вероятность того, что из яйца выведется петушок, равна 0,6. В инкубатор заложили 6 яиц. Найти ряд и функцию распределения числа петушков, которые выведутся из этих 6 яиц. Вычислить вероятность того, что число петушков не меньше 5. 227. Имеется 5 семян редкого растения со всхожестью 60%. Семена высеян по очереди (каждое следующее высевается только в том случае, если предыдущее не взошло). Составить ряд и функцию распределения числа использованных семян. Найти вероятность того, что число использованных семян больше 1 и меньше 3. Проиллюстрировать графически. Найти среднее число использованных семян. 228. Производится последовательное испытание 5 приборов на надежность. Каждый следующий прибор испытывается в том случае, если предыдущий оказался надежным. Построить ряд и функцию распределения случайного числа испытанных приборов, если вероятность выдержки испытания для каждого из них равна 0,9. Найти вероятность того, что придется испытывать не менее 2 и не более 4 приборов. 229. При бросании трех игральных костей игрок выигрывает: 18 руб., если на всех костях выпадает по 6 очков; 1 руб. 40 коп., если на двух костях выпадает по 6 очков и по 20 коп., если на одной кости выпадает 6 очков. Какова должна быть ставка за участие в игре, чтобы игра была безобидной. Построить ряд и функцию распределения выигрыша. 230. Выпущено 10000 билетов денежной лотереи. Разыгрывается 2 выигрыша по 5000 рублей, 8 по 1000, 170 по 100 рублей, 350 по 50 рублей и 750 по 10 рублей. Составить ряд и функцию распределения стоимости выигрыша для владельца одного лотерейного билета. Вычислить «справедливую» цену одного билета.
В задачах 231-340 заданы математическое ожидание а и среднее квадратическое отклонение
|

 .
.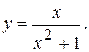 72.
72.  73.
73. 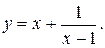 74.
74. 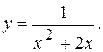
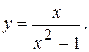 76.
76. 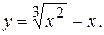 77.
77. 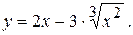
 79.
79. 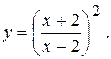 80.
80. 
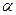 . На стороне ВС найти точку Е так, чтобы параллелограмм АДЕF, у которого точки Д и F лежат соответственно на стороне АВ и АС имел наибольшую площадь.
. На стороне ВС найти точку Е так, чтобы параллелограмм АДЕF, у которого точки Д и F лежат соответственно на стороне АВ и АС имел наибольшую площадь.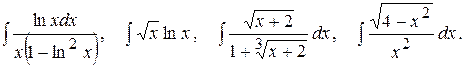

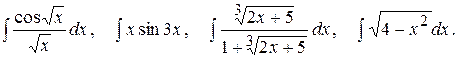
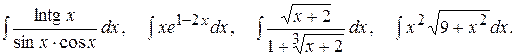

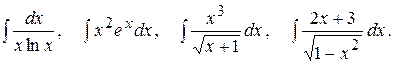

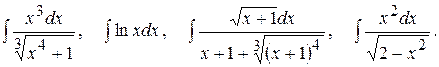

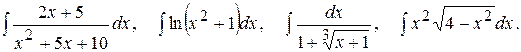
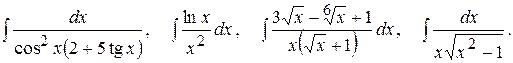
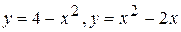 . 102.
. 102.  .
.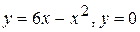 . 104.
. 104.  .
.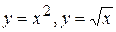 . 106.
. 106. 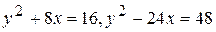 .
.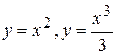 . 108.
. 108.  .
.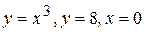 . 110.
. 110.  .
. 112.
112. 
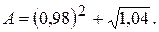 114.
114. 
 116.
116. 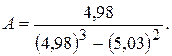
 118.
118. 
 120.
120. 
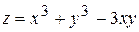 , D: x = 0, x = 4, y = 0, y = 4.
, D: x = 0, x = 4, y = 0, y = 4.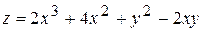 , D:
, D:  , y = 4, x
, y = 4, x 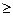 0.
0. , D: y = 0, x = 2, y = x +2.
, D: y = 0, x = 2, y = x +2.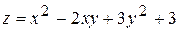 , D: y = 0,
, D: y = 0, 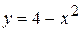 .
. , D: x = 0, y = 0, x + y = 3.
, D: x = 0, y = 0, x + y = 3.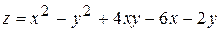 , D: x = 0, y = 0, x + y = 4.
, D: x = 0, y = 0, x + y = 4.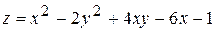 , D: x = 0, y = 0, x + y = 5.
, D: x = 0, y = 0, x + y = 5.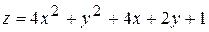 , D: x = 0, y = 0, x + y = -2.
, D: x = 0, y = 0, x + y = -2.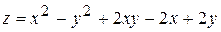 , D: y = x + 2, y = 0, x = 2.
, D: y = x + 2, y = 0, x = 2. , D: y = x + 1, y = 0, x = 3.
, D: y = x + 1, y = 0, x = 3.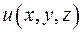 в точке
в точке  по направлению нормали к поверхности
по направлению нормали к поверхности 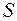 , образующей острый угол с положительным направлением оси
, образующей острый угол с положительным направлением оси 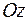 . Найти величину и направление наибольшего изменения скалярной функции в указанной точке
. Найти величину и направление наибольшего изменения скалярной функции в указанной точке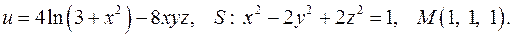
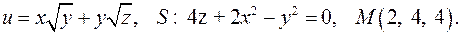
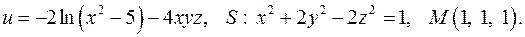
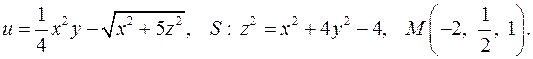
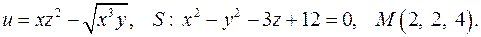
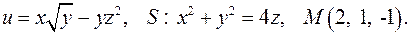
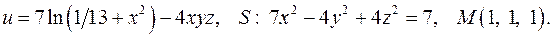

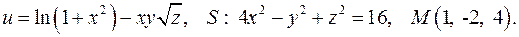
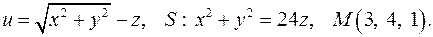
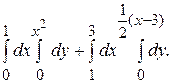 142.
142. 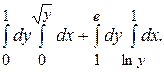
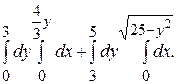 144.
144. 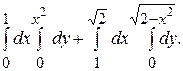
 146.
146. 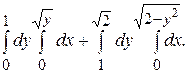
 148.
148. 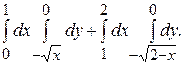
 150.
150. 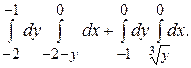
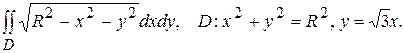
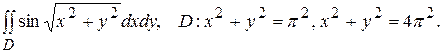


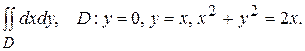

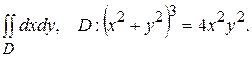

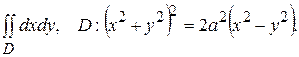

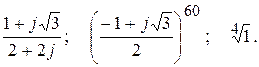





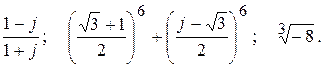

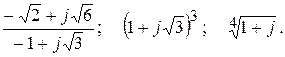
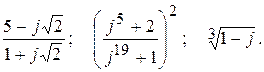

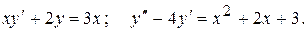

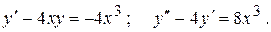
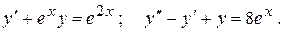
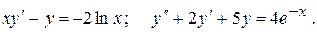
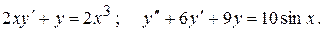

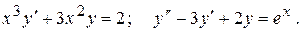
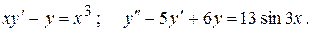
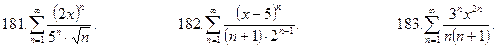


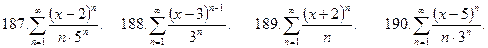
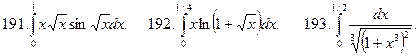

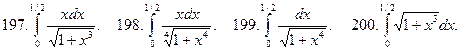
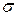 нормально распределенной случайной величины
нормально распределенной случайной величины  . Найти: 1) вероятность того, что
. Найти: 1) вероятность того, что 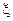 примет значение, принадлежащее интервалу (
примет значение, принадлежащее интервалу ( ); 2) вероятность того, что абсолютная величина отклонения
); 2) вероятность того, что абсолютная величина отклонения 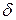 .
.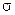 =2
=2
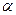 =9
=9
 =19
=19
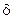 =3
=3



