Для бакалавров – заочников инженерного факультета 5 страница
По таблице производных находим:
Подставляем найденный производные в формулу (1) и делаем обратную замену:
Итак, мы нашли Распишем по этой формуле
Подставляем найденные производные в
Пример 13 (к задачам 71-80). Провести полное исследование функции Решение. Исследование предлагается провести в несколько этапов, которые озаглавим соответствующим образом. 1. Исследование на непрерывность, построение асимптот. Начинаем с области определения функции: функция определена (следовательно, непрерывна) везде, кроме точки х = 0. Исследуем характер разрыва в точке х = 0.
Таким образом, в точке х = 0 функция терпит разрыв II рода с бесконечным скачком, а прямая х = 0 (т.е. ось OY) является вертикальной асимптотой графика функции. Найдем наклонные (в частном случае горизонтальные) асимптоты. Известно, что уравнение наклонных асимптот имеет вид
Следовательно,
2. Иссследование с помощью первой производной (возрастание, убывание, экстремум). Находим производную функции по формуле производной дроби:
Итак, Находим критические точки, т.е. точки, «подозрительные» на экстремум. Имеются два источника появления критических точек: точки, в которых производная равна нулю, или не существует.
Итак, получили три критические точки, которыми числовая прямая разбивается на интервалы, в каждом из которых производная имеет определенный знак. Удобно изобразить исследование с помощью первой производной на числовой прямой следующим образом:
Берем в каждом интервале любую точку и выясняем знак производной (ставим соответственно + или -). На интервалах Этот схематический рисунок удобен тем, что стрелки как бы намечают траекторию графика функции (см. график в конце примера). Кроме этого, он наглядно иллюстрирует достаточный признак экстремума функции в точке: если при переходе через критическую точку производная меняет знак, то в этой точке экстремум есть, причем, если знак меняется с «+» на «–», то имеется максимум, если с «–» на «+», то минимум. Глядя на рисунок, это легко понять: при х = –1 функция имеет максимум, при х = 1 – минимум. Найдем
Замечание: Разумеется, точка х = 0 никак не может быть точкой экстремума, поскольку в этой точке функция терпит разрыв. Однако, для нахождения интервалов возрастания и убывания она необходима и потому её тоже считаем критической. То же замечание относится и к исследованию с помощью
3. Исследование функции с помощью второй производной (выпуклость, вогнутость, перегиб). Исследование функции на выпуклость, вогнутость и перегиб с помощью второй производной проводится по той же схеме, по которой с помощью первой производной проводится исследование функции на убывание, возрастание и экстремум.
Имеются два источника точек, «подозрительных» на перегиб:
На интервале Теперь строим график функции на основании проведенного исследования.
Пример №14. (для задач 81-90). На странице книги печатный текст должен занимать S см2 . Верхнее и нижнее поля должны быть а см, а правое и левое – b см. Какими должны быть наиболее экономные размеры страницы?
Обозначим ширину текста за x. Тогда, поскольку площадь текста равна S, высота текста равна y = S/x. Из чертежа ясно, что ширина m страницы будет равна m = x + 2 b, высота h страницы равна h = S/ x + 2 а, а площадь страницы
Итак, получили задачу на экстремум (минимум) функции
Сначала находим критические точки (точки, «подозрительные» на экстремум). Таковыми могут быть лишь те, в которых производная
Если
Из физических соображений ясно, что величина x, ширина текста, должна быть положительным числом. Поэтому из трех критических точек нас интересует лишь точка Итак, страница будет экономной (т.е. ее площадь будет наименьшей), если ширина текста Соответственно этому, ширина самой страницы
а ее высота Эти формулы не очень наглядны. Для наглядности найдем отношение высоты к ширине страницы:
Итак, получаем ответ в более наглядной форме: размеры самой экономной страницы должны быть такими, чтобы отношение ее высоты к ширине равнялось отношению верхнего или нижнего поля к правому или левому.
Пример 15 (к задачам 91-100). Найти неопределенные интегралы:
Решение. Существуют два общих метода интегрирования: метод замены переменной (иначе он называется методом подстановки) и метод интегрирования по частям. Метод замены переменной схематично можно записать в виде следующей формулы:
Метод интегрирования по частям определяется формулой:
где Когда и как применять каждую из формул рассмотрим на примерах. а) Обратим внимание на формулу (2). Во-первых, отметим, что эту формулу можно применять как слева направо, так и справа налево. Если иметь в виду применение формулы (2) справа налево, т.е. в виде (используя в первоначальном задании привычную переменную х):
То можно заметить, что формулу (4) следует применять всякий раз, когда в заданном интеграле мы увидим некоторую функцию g (x) и её производную Обратимся к первому интегралу а) и заметим, что под знаком интеграла присутствует функция g (x) = ln x и её производная
б) Второй интеграл вычисляется по формуле интегрирования по частям. Почему? Дело в том, что, как уже было сказано, замена переменной уместна, если под знаком интеграла мы заметили некоторую функцию и её производную В нашем примере б) под знаком интеграла присутствуют две функции разной природы:
Просматривая приведенную запись решения увидим, во-первых, что формула (3) сводит вычисление исходного интеграла к вычислению двух, но более простых интегралов: один – при нахождении функции v, а второй – в результате применения самой формулы. Во-вторых, формула действительно разъединила две функции Следующие два примера реализуют применение формулы замены переменной слева направо. в) В третьем интеграле обратим внимание на присутствие иррациональностей, т.е. радикалов, причем под знаком радикалов различной степени стоит линейная функция (2 х + 3). Такие иррациональности, когда под знаком радикалов различной степени стоят дробно-линейные (в частном случае – линейные) функции, называются простейшими иррациональностями. Такие иррациональности потому и называются простейшими, что очевидная подстановка приводит к цели, а именно, полагаем 2 х + 3 = t 6 c тем, чтобы одновременно избавиться от обоих радикалов. Проведем теперь все преобразования:
Таким образом, пока сделан один шаг вперед – интеграл от иррациональной функции сведен к интегралу от дробно-рациональной функции (ДРФ), т.е. к отношению двух многочленов – к более простой задаче. Займемся теперь полученным интегралом. Под знаком интеграла стоит ДРФ, причем неправильная, т.к. степень числителя больше степени знаменателя. Как известно, всякая неправильная ДРФ может быть представлена в виде суммы некоторого многочлена и правильной ДРФ (у которой степень числителя строго меньше степени знаменателя). Это представление осуществляется делением уголком
Итак,
г) Следующий пример показывает ещё один прием избавления от иррациональности, на сей раз от квадратической. При этом следует помнить, что для интегрирования квадратических иррациональностей имеются так называемые подстановки Эйлера. Они имеются в любых учебниках. Вместе с тем, иногда удобны тригонометрические подстановки. Обратим внимание на заданный интеграл. В принципе, задача любой подстановки заключается в избавлении от иррациональности. Для этого используются известные формулы тригонометрии:
Вернемся к нашему примеру. На основании приведенных формул будут ясна логика нижеприведенных преобразований:
Вычислим теперь интеграл В соответствии с теорией – это интеграл от правильной ДРФ, знаменатель которой представлен в каноническом виде и которую представляем в виде суммы простейших дробей:
Для нахождения коэффициентов А,В,С,Д приводим дроби к общему знаменателю:
Дроби равны, знаменатели равны, следовательно, равны и числители:
Равенство (5), которое на самом деле – тождество, является исходным для определения коэффициентов А,В,С,Д. В связи с этим, имеется два способа определения коэффициентов А,В,С,Д. 1 способ: Раскрываем скобки в тождество (4):
Многочлены равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях аргумента, поэтому Т.е. получаем СЛАУ относительно неизвестных А, В, С, Д. Эту систему решаем методом Гаусса:
~
R(A) = R(A*) = 4
В = –Д = – 1/4 А = 1/4, В = –1/4, С = 1/4, Д = 1/4.
2 способ. Возвращаемся к тождеству (5) и поскольку оно тождество, то справедливо при всех значениях неизвестного х. Нам необходимо вычислить значения четырех неизвестных, поэтому возьмем четыре значения х. Разумеется, желательно эти значения выбирать с выгодой. «Выгодными» значениями являются у = – 1, у = +1. Остальные два значения возьмем любыми: у = 0 и у = 2. Получаем:
Итак,
Процесс интегрирования закончен - надо вернуться к старой переменной – это оставляем читателю, - хотя бы для того, чтобы посмотреть, каким громоздким может быть окончательный результат.
Пример 16(к задачам 101-110). Вычислить площадь фигуры, ограниченной линиями: у = х 3 – 1, у = 1 – х 2, х = 0. Решение.
Фигура (см. чертеж) ограничена: сверху – графиком функции у = 1 – х 2, снизу – графиком функции у = х 3 – 1, слева – прямой х = 0, справа прямой х = 1 (которая выродилась в точку). поэтому, на основании геометрического смысла определенного интеграла площадь фигуры
Пример 17 (к задачам 111-120). Вычислить число Решение. Сначала отметим, что замена приращения функции её дифференциалом представляет собой самый «грубый» метод приближенных вычислений. Вместе с тем велико его теоретическое значение и практическая простота – почти все вычисления проводятся без привлечения вычислительных средств. Сущность метода заключается в следующем: пусть требуется вычислить число А – значение функции Далее применяют формулу приближенных вычислений с помощью дифференциала:
(14) где Обратимся теперь к нашему примеру. Видим, что в выражение для числа А входят два «плохих» числа х 1 = 5,03 и у 1 = 4,98 и, таким образом, можно записать, что число А является значением функции
И вычисляем значения этих частных производных в точке (5,5):
Подставляя полученные значения в формулу (14) получаем окончательный результат:
Пример 18 (к задачам 121-130). Найти наибольшее и наименьшее значения функции Решение. Сделаем чертеж.
Тогда С (1/2,1) – критическая и принадлежит области G. Можно, конечно, использовать достаточный признак экстремума и выяснить имеется ли в действительности в точке С максимум или минимум. Мы, однако, предпочтем более простой путь – вычислим значение функции в точке С, а затем сравним с исследованием на границе:
Приступаем к исследованию функции на экстремум на границе области Д. Граница состоит из трех отрезков линий. Рассмотрим их по порядку. 1) ОА: х = 0, На этой границе функция
|

 . (1)
. (1) ;
;  ;
;  .
.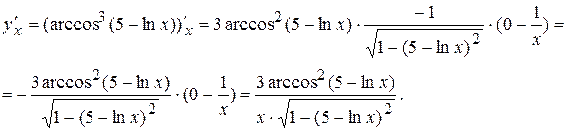
 Найдём вторую производную заданной функции, то есть продифференцируем полученную функцию
Найдём вторую производную заданной функции, то есть продифференцируем полученную функцию  . Для того, чтобы найти производную этой функции воспользуемся правилами дифференцирования частного:
. Для того, чтобы найти производную этой функции воспользуемся правилами дифференцирования частного: 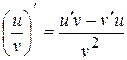 .
. :
: Производную
Производную  находим по вышеизложенному принципу:
находим по вышеизложенному принципу: Производную
Производную  будем находить по правилу дифференцирования произведения:
будем находить по правилу дифференцирования произведения:  .
.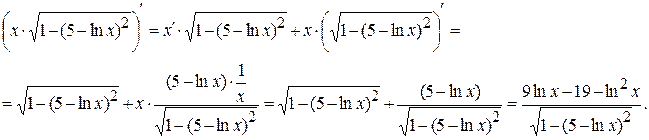

 и построить ее график.
и построить ее график. ,
, 
 , где
, где  , а после нахождения углового коэффициента
, а после нахождения углового коэффициента  находим
находим  В нашем случае получаем:
В нашем случае получаем:
 - наклонная асимптота.
- наклонная асимптота.



 производная
производная  , следовательно функция
, следовательно функция  возрастает (стрелки направлены вверх); соответственно, на интервалах (-1,0) и (0,1)
возрастает (стрелки направлены вверх); соответственно, на интервалах (-1,0) и (0,1)  , следовательно функция убывает.
, следовательно функция убывает. Итак, точки А1(–1, –2) и А2(1,2) – точки максимума и минимума графика функции.
Итак, точки А1(–1, –2) и А2(1,2) – точки максимума и минимума графика функции. .
.
 не существует. В нашем примере
не существует. В нашем примере  не существует при х = 0. Вновь строим аналогичный чертеж:
не существует при х = 0. Вновь строим аналогичный чертеж:
 , следовательно функция
, следовательно функция  , следовательно функция вогнутая. Несмотря на то, что в точке х = 0 выпуклость сменяется вогнутостью, эта точка не является точкой перегиба, поскольку в точке х=0 функция разрывна.
, следовательно функция вогнутая. Несмотря на то, что в точке х = 0 выпуклость сменяется вогнутостью, эта точка не является точкой перегиба, поскольку в точке х=0 функция разрывна.
 Решение. Сделаем схематичный чертеж страницы и размеры текста на ней (внутренний прямоугольник).
Решение. Сделаем схематичный чертеж страницы и размеры текста на ней (внутренний прямоугольник). .
.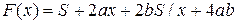 .
. равна нулю или не существует. Находим
равна нулю или не существует. Находим  .
.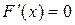 , то
, то  ;
;  ;
; 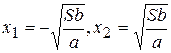 .
.

 Производная F ’’(x) при переходе через эту точку слева направо меняет знак с минуса на плюс, т.е. в этой точке убывание сменяется возрастанием функции, следовательно, функция F(x) в этой точке имеет минимум.
Производная F ’’(x) при переходе через эту точку слева направо меняет знак с минуса на плюс, т.е. в этой точке убывание сменяется возрастанием функции, следовательно, функция F(x) в этой точке имеет минимум. , а его высота
, а его высота 
 ,
, .
. .
.
 (2)
(2)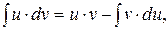 (3)
(3) - некоторые функции.
- некоторые функции. (4)
(4) , - тогда применяем подстановку g (x) = t.
, - тогда применяем подстановку g (x) = t. Поэтому:
Поэтому:
 . Нет ни одной табличной формулы, связывающей функции разной природы. Поэтому естественно возникает необходимость разъединить эти функции. Такую роль и исполняет формула интегрирования по частям:
. Нет ни одной табличной формулы, связывающей функции разной природы. Поэтому естественно возникает необходимость разъединить эти функции. Такую роль и исполняет формула интегрирования по частям:









 (5)
(5)




 ~
~ 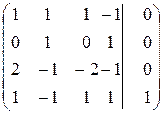
 ~
~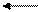
 ~
~  ~
~  ~
~ .
. система имеет единственное решение. Для нахождения его составим систему, соответствующую ступенчатой матрице:
система имеет единственное решение. Для нахождения его составим систему, соответствующую ступенчатой матрице:






 приближенно с помощью дифференциала функции двух переменных.
приближенно с помощью дифференциала функции двух переменных. в некоторой точке
в некоторой точке  . Точка
. Точка  - «плохая», т.е. устно, без вычислительных средств (например, калькулятора) подсчитать
- «плохая», т.е. устно, без вычислительных средств (например, калькулятора) подсчитать  трудно. Тогда находят близкую, «хорошую» точку
трудно. Тогда находят близкую, «хорошую» точку  вычисления в которой выполняются легко.
вычисления в которой выполняются легко.

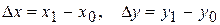 - приращения аргументов,
- приращения аргументов,  ,
,  - значения частных производных функции в «хорошей» точке (х0,у0).
- значения частных производных функции в «хорошей» точке (х0,у0). в точке (х 1, у 1), где х 1 = 5,03 и у 1 = 4,98. Тогда выбираем близкие два числа х0=5; у0=5, т.е. «хорошую» точку (5;5) и проводим вычисления по формуле (14) в этой точке. Предварительно получаем:
в точке (х 1, у 1), где х 1 = 5,03 и у 1 = 4,98. Тогда выбираем близкие два числа х0=5; у0=5, т.е. «хорошую» точку (5;5) и проводим вычисления по формуле (14) в этой точке. Предварительно получаем: Находим частные производные:
Находим частные производные: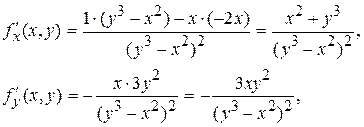


 в замкнутой области G, ограниченной линиями х = 0, у = х, х + у = 2.
в замкнутой области G, ограниченной линиями х = 0, у = х, х + у = 2. Область G представляет собой треугольник ОАВ. Следует обратить внимание на замкнутость области G (т.е. граница принадлежит области), поскольку в замкнутой области функция обязательно достигает своих наименьшего и наибольшего значений, при этом они достигаются либо в точках экстремума, либо на границе области. Поэтому сначала найдем стационарные точки – точки «подозрительные» на экстремум. Для этого находим частные производные и приравниваем их к нулю – получим систему линейных уравнений:
Область G представляет собой треугольник ОАВ. Следует обратить внимание на замкнутость области G (т.е. граница принадлежит области), поскольку в замкнутой области функция обязательно достигает своих наименьшего и наибольшего значений, при этом они достигаются либо в точках экстремума, либо на границе области. Поэтому сначала найдем стационарные точки – точки «подозрительные» на экстремум. Для этого находим частные производные и приравниваем их к нулю – получим систему линейных уравнений:

 .
. Исследуем её на экстремум:
Исследуем её на экстремум: 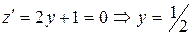 . Получили точку D (0;1/2). Она принадлежит отрезку ОА. Вычисляем z (D)=
. Получили точку D (0;1/2). Она принадлежит отрезку ОА. Вычисляем z (D)= 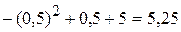 . На отрезке ОА функция z =
. На отрезке ОА функция z =  может достигать наибольшего и наименьшего значений либо в точках экстремума, либо на границе, т.е.в точках O (0,0) или А (0,2). Вычисляем z(O) = 5; z(А) = – 4 + 2 + 5 = 3.
может достигать наибольшего и наименьшего значений либо в точках экстремума, либо на границе, т.е.в точках O (0,0) или А (0,2). Вычисляем z(O) = 5; z(А) = – 4 + 2 + 5 = 3.


