Для бакалавров – заочников инженерного факультета 1 страница
Кафедра высшей математики Л. Б. Винникова
ВЫСШАЯ МАТЕМАТИКА
ВЫСШАЯ МАТЕМАТИКА ПРОГРАММА И КОНТРОЛЬНЫЕ РАБОТЫ для бакалавров – заочников инженерного факультета направление подготовки 13.03.02.«Электроэнергетика и электротехника» профиль: «Электроснабжение»
Рязань 2015
Учебно - практическое пособие обсуждено на заседании кафедры высшей математики Рязанского государственного агротехнологического университета и рекомендовано опубликованию «» марта 2015 г. Протокол №
Зав. кафедрой высшей математики, канд. физ.-мат. наук, доцент Е.И. Троицкий
Учебно – практическое пособие утверждено методической комиссией факультета экономики и менеджмента Рязанского государственного агротехнологического университета «___» ________2015г. Протокол №__
Председатель методической комиссии факультета экономики и менеджмента И. В. Лучкова
Методические указания по выполнению контрольных работ по математике для бакалавров-заочников инженерного факультета./Л. Б. Винникова, Рязань: РГАТУ, 2015.- 102 с.
Учебно – практическое пособие предназначено для студентов – заочников первого,второго курса инженерного факультета по направлению подготовки 13.03.02.«Электроэнергетика и электротехника». Материал учебного пособия соответствует Федеральным государственным образовательным стандартам третьего поколения по указанному направлению подготовки. Пособие содержит программу дисциплины «Высшая математика», список рекомендуемой литературы, 10 вариантов заданий контрольных работ. Даны примеры выполнения всех заданий контрольных работ, методические рекомендации по оформлению и выполнению контрольных работ.
Рецензенты: Е. И. Троицкий, к. ф.-м. н., доцент, зав. кафедры высшей математики Гришин И. И., д.т.н., профессор, кафедры электротехники, электрооборудования и автоматики
СОДЕРЖАНИЕ.
Общие методические указания.
Пособие рассчитано на студентов заочной формы обучения, но может быть использовано в качестве дополнительного учебно-методического пособия и студентами, обучающимися на очном отделени. При этом считается, что наиболее эффективным способом изучения курса высшей математики является самостоятельная работа студента: чтение учебников, решение задач, выполнение контрольных заданий. Если в процессе изучения материала или при решении задач у студента возникнут трудности, то он может обратиться за консультацией к преподавателю кафедры высшей математики. С целью упорядочения изучения курса и для систематической и своевременной проверки (и самопроверки) качества усвоения материала студент обязан выполнить 3 контрольные работы и 1 курсовую работу. Выполненные работы присылаются (или доставляются лично) на кафедру высшей математики. После рецензирования студент может забрать свои работы для изучения замечаний и подготовки к экзамену или к защите курсовой работы.
Каждый студент выполняет тот вариант контрольных работ, который соответствует его учебному шифру в соответствии с таблицей (информацию о номере своего варианта можно получить у методиста или преподавателя).
Рабочая программа курса высшей математики. Рабочая программа составлена с учетом требований федерального государственного образовательного стандарта высшего профессионального образования (ФГОС ВПО) третьего поколения по направлению подготовки 110800 «Агроинженерия» (квалификация «бакалавр»). Рабочая программа разбита на темы, которые, в свою очередь, разбиты на отдельные вопросы. Эти вопросы являются теоретическим вопросами экзаменационных билетов. Содержание программы. I курс. Тема №1. Определители. Матрицы и их применение к решению систем линейных алгебраических уравнений (СЛАУ). 1. Определение определителя произвольного прядка. Миноры, алгебраические дополнения. 2. Свойства определителей, их применение к практическому вычислению определителей. 3. Определение матрицы, действия с матрицами: сложение, умножение на число, умножение двух матриц, вычисление обратной матрицы. 4. Матричная запись СЛАУ. Матричный метод и метод Крамера решения СЛАУ. 5. Ранг матрицы. Элементарные преобразования матриц. Ступенчатые матрицы. 6. Метод Гаусса решения СЛАУ, различные случаи (на примерах). Теорема Кронекера-Капелли. Исследование однородных систем.
Тема №2. Линейная и векторная алгебра. Аналитическая геометрия. 7. Определение вектора, длина вектора, нуль-вектор. Линейные операции над векторами. Коллинеарность двух векторов. 8. Линейная зависимость и независимость векторов. Иллюстрация этих понятий на примере векторов на плоскости и в пространстве. 9. Скалярное произведение векторов и его свойства. Скалярное произведение векторов в координатной форме. 10. Векторное произведение векторов и его свойства. Векторное произведение в координатной форме. 11. Смешанное произведение векторов и его свойства. Смешанное произведение векторов в координатной форме. 12. Различные уравнения плоскости в пространстве: с опорной точкой и вектором нормали, через три точки, общее и его частные случаи, в отрезках на осях. 13. Расстояние от точки до плоскости. 14. Взаимное расположение двух плоскостей: угол между двумя плоскостями, условия параллельности и перпендикулярности двух плоскостей. 15. Различные уравнения прямой линии в пространстве: с опорной точкой и направляющим вектором, параметрические, канонические, через две точки. 16. Взаимное расположение двух прямых в пространстве: угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых в пространстве. 17. Взаимное расположение прямой и плоскости в пространстве: угол между прямой и плоскостью, условия параллельности и перпендикулярности прямой и плоскости, нахождение точки пересечения прямой и плоскости. 18. Различные уравнения прямой линии на плоскости (изложение рекомендуется проводить с использованием результатов выводов уравнений прямой в пространстве и плоскости в пространстве): с опорной точкой и направляющим вектором, через две точки, с угловым коэффициентом, с опорной точкой и вектором нормали, общее уравнение и его частные случаи, в отрезках на осях. Расстояние от точки до прямой. 19. Взаимное расположение двух прямых на плоскости: угол между двумя прямыми (вычисление различными способами), условия параллельности и перпендикулярности двух прямых. 20. Кривые второго порядка. Канонические уравнения эллипса. Эксцентриситет, директрисы. 21. Каноническое уравнение гиперболы. Эксцентриситет, директрисы, асимптоты. 22. Каноническое уравнение параболы. 23. Полярные координаты на плоскости, связь декартовых и полярных координат точки. 24. Цилиндрические и сферические координаты; связь с декартовыми.
Тема №3. Предел функции. 25. Понятие предела в функции в точке. Бесконечно малая функции, теорема о замене б. малой функции, ей эквивалентной. Свойства пределов. 26. Раскрытие неопределенностей от алгебраических функций. 27. Первый замечательный предел (вывод), следствия из него (цепочка эквивалентностей). 28. Второй замечательный предел и следствия из него. Натуральные логарифмы. Экспонента. 29. Непрерывность функции в точке, различные определения. Односторонние пределы. 30. Классификация точек разрыва. Вертикальные асимптоты.
Тема №4. Дифференциальное исчисление функций одной переменной. 31. Определение производной функции. Физический, геометрический и экономический смысл производной. Эластичность функций. 32. Уравнение касательной и нормали к графику функции. 33. Дифференциал функции, геометрический смысл. 34. Производная суммы, произведения, частного. Производная сложной и обратной функций.
Тема №5. Приложения дифференциального исчисления. 35. Основные теоремы дифференциального исчисления: Ферма, Ролля, Лягранжа. 36. Формула Тейлора (Маклорена) с остаточным членом в форме Лагранжа. Формула Маклорена для функций е х, sin x, cos x, (1+ х) α. 37. Исследование функций с помощью первой производной – условия постоянства, монотонности. 38. Экстремум функций. Необходимые условия экстремума. Два достаточных условия экстремума. 39. Исследование функции с помощью второй производной – выпуклость, вогнутость, перегиб. 40. Наклонные асимптоты графика функции.
Тема №6. Неопределенный интеграл. 41. Первообразная функция. Неопределенный интеграл и его свойства. 42. Интегрирование заменой переменной. 43. Интегрирование по частям. 44. Классы интегрируемых функций. Интегрирование простейших дробей. 45. Интегрирование простейших иррациональностей. 46. Интегрирование тригонометрических функций. Тригонометрические подстановки.
Тема №7. Определенный интеграл. 47. Задача о вычислении площади криволинейной трапеции, приводящая к понятию определенного интеграла. Определение определенного интеграла и его геометрический смысл. Свойства определенного интеграла. 48. Интеграл с переменным верхним пределом, его свойства. Формула Ньютона-Лейбница. 49. Замена переменной и интегрирование по частям в определенном интеграле. 50. Несобственные интегралы I рода – определение, вычисление, признаки сходимости.
Тема №8. Функции нескольких переменных (ФНП). 51. Определение ФНП. Геометрическое изображение функций двух переменных. Линия уровня. Примеры. Частные и полные приращения ФНП. Частные производные, полный дифференциал ФНП. 52. Экстремум ФНП – определение, необходимые условия, достаточные условия экстремума функции двух переменных. Наибольшее и наименьшее значения ФНП в замкнутом множестве. 53. Производная по направлению. Градиент. Уравнения касательной плоскости и нормали к поверхности.
Тема №9. Кратные интегралы. 54. Задача о вычислении объема тела, приводящая к понятию двойного интеграла. Определение двойного интеграла, его геометрический смысл. 55. Свойства двойного интеграла. Вычисление двойного интеграла. 56. Замена переменных в двойном интеграле, якобиан. Двойной интеграл в полярных координатах. 57. Задача о вычислении массы тела, приводящая к понятию тройного интеграла. Определение тройного интеграла. Свойства тройного интеграла. 58. Вычисление тройного интеграла. 59. Замена переменных в тройном интеграле, якобиан. Тройной интеграл в цилиндрических и сферических координатах. 60. Приложения кратных интегралов.
Тема №10. Комплексные числа. 61. Расширенное понятие о числе. Мнимые и действительные числа. 62. Комплексные числа, действия с ними. Алгебраическая форма записи комплексного числа. 63. Геометрическое изображение комплексных чисел в декартовой системе координат. Модуль и аргумент комплексного числа. Тригонометрическая форма комплексного числа. 64. Формула Эйлера. Показательная форма комплексного числа. 65. Действия над комплексными числами в тригонометрической форме. Формулы Муавра. 66. Элементарные функции комплексного переменного.
Тема №11 Обыкновенные дифференциальные уравнения (ДУ). 67. Основные понятия ДУ: частное и общее решения, геометрический смысл решения ДУ I порядка, метод изоклин. 68. ДУ с разделяющимися переменными. 69. Однородные ДУ I порядка. 70. Линейные ДУ (ЛДУ) I порядка – два метода решения. ДУ Бернулли. 71. ДУ в полных дифференциалах. 72. ЛДУ высших порядков, основные свойства. Линейная зависимость и независимость решений ЛОДУ, определитель Вронского, общее решение ЛОДУ. 73. ЛОДУ с постоянными коэффициентами, характеристическое уравнение. Структура общего решения ЛОДУ в различных случаях корней характеристического уравнения. 74. Линейные неоднородные ДУ (ЛНДУ), структура общего решения, теорема о наложении решений. Подбор решений ЛНДУ по виду правой части.
Тема №12. Числовые и степенные ряды. 75. Числовой ряд – определение, частичные суммы, сумма ряда. Простейшие свойства сходящихся числовых рядов. 76. Необходимый признак сходимости ряда. 77. Признак Даламбера. 78. Интегральный признак сходимости рядов. Эталонный ряд 79. Предельный признак сравнения рядов. 80. Знакопеременные и знакочередующиеся ряды. Абсолютная и условная сходимости. Теорема Лейбница, её применение к оценке остатка ряда. 81. Функциональный ряд, область сходимости. Степенной ряд. Теорема Абеля. Дифференцирование и интегрирование степенных рядов. 82. Единственность разложения функций в степенной ряд. Ряды Тейлора (Маклорена). Разложение в ряд Маклорена функций е х, sin x,cos x,
Тема №13. Теория вероятностей. 83. Основные понятия теории вероятностей: случайное событие, пространство элементарных событий. Алгебра событий. Диаграммы Эйлера-Венна. 84. Вероятность случайного события. Аксиомы вероятностей, следствия из них, теорема сложения. 85. Примеры вероятных пространств – геометрические вероятности и классическое определение вероятности. Формулы комбинаторики. 86. Теорема умножения вероятностей. 87. Формула полной вероятности и формула Байеса. 88. Повторные испытания, формула Бернулли. Асимптотические формулы для формулы Бернулли: локальная теорема Муавра-Лапласа, интегральная теорема Лапласа, формула Пуассона. 89. Случайные величины (СВ), основные понятия. Ряд распределения и функция распределения дискретных СВ (ДСВ). 90. Функция распределения непрерывных СВ (НСВ). Общие свойства функции распределения. 91. Плотность вероятности и ее свойства. 92. Математическое ожидание СВ и его свойства. 93. Дисперсия СВ и ее свойства. Среднее квадратическое отклонение. 94. Примеры законов распределения; биноминальный закон, его свойства; закон Пуассона и его свойства; простейший поток событий. 95. Равномерное распределение и его свойства. Нормальное распределение и его свойства. 96. Предельные теоремы теории вероятностей. Лемма Маркова. Неравенство и теорема Чебышева. Неравенство и теорема Бернулли. 97. Понятие о центральной предельной теореме. Тема №14. Математическая статистика. 98. Предмет математической статистики. Генеральная совокупность и выборка. Вариационный ряд и его геометрическое изображение – полигон и гистограмма. 99. Точечные оценки параметров распределения. Гипотетическая интерпретация выборочных данных (ГИВД). Требования к точечным оценкам. 100. Выборочная средняя арифметическая и ее свойства. 101. Выборочная дисперсия и ее свойства, исправленная выборочная дисперсия. 102. Интервальные оценки параметров распределения. Доверительный интервал, доверительная вероятность. Построение доверительного интервала для неизвестного мат ожидания при известной дисперсии. 103. Распределение хи-квадрат Пирсона и его простейшие свойства. Построение доверительного интервала для неизвестной дисперсии. 104. Распределение Стьюдента и его простейшие свойства. Построение доверительного интервала для неизвестного мат ожидания при неизвестной дисперсии. 105. Критерии согласия. Критерий согласия хи-квадрат Пирсона. 106. Распределение Фишера-Снедекора и его простейшие свойства. Понятие о дисперсионном анализе. Схема применения однофакторного дисперсионного анализа. 107. Элементы корреляционного анализа. Метод наименьших квадратов для определения параметров прямых регрессии y на x и x на y. Коэффициент корреляции и его свойства, шкала Чеддока.
Задания контрольных работ. Каждый студент выполняет тот вариант контрольных работ, который соответствует его учебному шифру в соответствии с таблицей (информацию о номере своего варианта можно получить у методиста или преподавателя). Контрольные работы выполняются в ученических тетрадях (каждая - в отдельной) и сдаются до начала сессии на проверку преподавателю. Перед решением каждой задачи контрольной работы следует записать её условие. Решение задач следует излагать достаточно подробно, делая соответствующие ссылки на теорию с указанием необходимых теорем и формул. Контрольная работа №1. Тема №1. Определители. Матрицы и их применение к решению систем линейных алгебраических уравнений (СЛАУ). В задачах 1-10 вычислить определитель четвертого порядка.
1.
4. 8.
В задачах 11-20 требуется решить СЛАУ (систему линейных алгебраических уравнений) по формулам Крамера и методом Гаусса.
11.
14.
17.
20.
Тема №2. Линейная и векторная алгебра. Аналитическая геометрия.
В задачах 21-30 даны координаты вершин пирамиды АВСД. Найти: 1) косинус угла между ребрами АВ и АД, 2) площадь грани АВС, 3) объем пирамиды АВСД, 4) длину высоты пирамиды, проведенной из точки Д.
21. А(-2,1,2), В(4,0,0), С(3,2,7), Д(1,3,2). 22. А(1,-1,6), В(1,-2,1), С(-2,1,0), Д(2,2,5). 23. А(1,-1,6), В(4,5,-2), С(-1,3,0), Д(6,1,5). 24. А(-5,-1,8), В(2,3,1), С(4,1,-2), Д(6,3,7). 25. А(5,1,-4), В(1,2,-1), С(3,3,-4), Д(2,2,2). 26. А(1,1,1), В(2,3,4), С(4,3,2), Д(3,2,4). 27. А(1,1,2), В(2,3,-1), С(2,-2,4), Д(-1,1,3). 28. А(2,-3,5), В(0,2,1), С(-2,-2,3), Д(3,2,4). 29. А(2,1,-2), В(3,3,3), С(1,1,2), Д(-1,-2,-3). 30. А(2,3,1), В(4,1,-2), С(6,3,7), Д(-5,-4,8). В задачах 31-40 даны координаты точек M,N,P,Q. Требуется: 1) составить уравнение прямой MN; 2) составить уравнение плоскости MNP; 3) составить уравнение прямой, проходящей через точку Q, перпендикулярно плоскости MNP; 4) найти точки пересечения этой прямой с плоскостью MNP; 5) найти расстояние от точки Q до плоскости MNP (двумя способами).
31. М (-3,-2,-4); N (-4,2,-7); Р (5,0,3); Q (-1,3,0). 32. М (2,-2,1); N (-3,0,-5); Р (0,-2,-1); Q (-3,4,7). 33. М (5,4,1); N (-1,-2,-2); Р (3,-2,2); Q (-5,5,4). 34. М (3,6,-2); N (0,2,-3); Р (1,-2,0); Q (-7,6,6). 35. М (1,-4,1); N (4,4,0); Р (-1,2,-4); Q (-9,7,8). 36. М (4,6,-1); N (7,2,4); Р (-2,0,-4); Q (3,1,-4). 37. М (0,6,-5); N (8,2,5); Р (2,6,-3); Q (5,0,-6). 38. М (-2,4,-6); N (0,-6,1); Р (4,2,1); Q (7,-1,-8). 39. М (-4,-2,-5); N (1,8,-5); Р (0,4,-4); Q (9,-2,-1).0 40. М (3,4,-1); N (2,-4,2); Р (5,6,0); Q (11,-3,-12).
В задачах 41-50 даны вершины треугольника МNР. Требуется найти: 1) длину стороны МN; 2) уравнение сторон МN и NР и их угловые коэффициенты; 3) угол N; 4) уравнение высоты РQ и её длину; 5) уравнение медианы МS; 6) уравнение прямой, проходящей через точку К параллельно стороне МN. Сделать чертеж.
41. М (-5,9); N (7,0); Р (5,14). 42. М (8,0); N (-4,-5); Р (-8,-2). 43. М (0,5); N (12,0); Р (18,8). 44. М (-1,7); N (11,2); Р (17,10). 45. М (5,8); N (-2,9); Р (-4,5). 46. М (6,1); N (-6,-4); Р (-10,-1). 47. М (-1,5); N (11,0); Р (17,8). 48. М (6,5); N (-6,0); Р (-10,3). 49. М (1,5); N (13,0); Р (13,8). 50. М (7,1); N (-5,-4); Р (-9,-1).
Тема №3. Предел функиии. В задачах 51-60 найти указанные пределы функций.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
Тема №4. Дифференциальное исчисление функций одной переменной. В задачах 61-70 найти 61. 64. 67.
|


 .
. .
.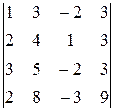 2.
2.  3.
3. 
 5.
5.  6.
6.  7.
7. 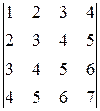
 9.
9.  10.
10. 
 12.
12.  13.
13. 
 15.
15.  16.
16. 
 18.
18.  19.
19. 



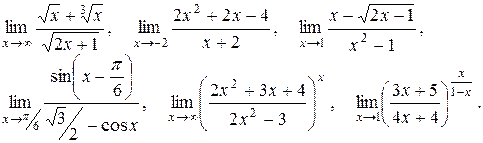
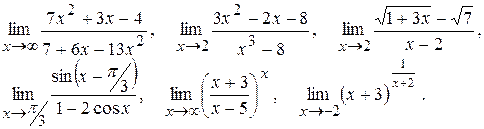


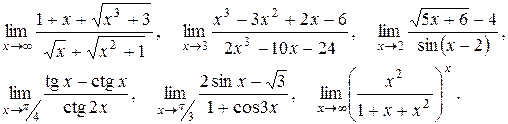




 указанной функции.
указанной функции. 62.
62.  63.
63. 
 65.
65. 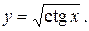 66.
66. 
 68.
68. 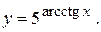 69.
69. 



