Для бакалавров – заочников инженерного факультета 3 страница
Тема №18. Математическая статистика. В задачах 241-250 предполагается, что проведен некоторый эксперимент, в результате которого получен набор данных. Требуется: 1. Построить вариационный ряд частот или относительных частот; 2. Изобразить геометрически вариационный ряд, построив гистограмму частот; 3. Вычислить точечные оценки параметров распределения; 4. Высказать гипотезу о виде закона распределения признака и применить критерий согласия хи-квадрат Пирсона на 5%-м уровне значимости; 5. Считая полученный набор данных генеральной совокупностью, сделать из этой совокупности выборку объема 10, для которой: а) вычислить точечные оценки параметров распределения – выборочную среднюю арифметическую б) найти доверительный интервал для генеральной средней на уровне значимости в) найти доверительный интервал для генеральной дисперсии.
241. Техническая длина стебля (см) у ста растений льна характеризуется таблицей:
242. Выработка продукции предприятиями в сравнении с предыдущей пятилеткой дается таблицей (в %):
243. Количество деталей, выработанных каждым из 100 рабочих в течение месяца:
244. 100 сверл были подвергнуты испытанию на твердость. При этом фиксировалась твердость лапки. Результаты испытания представлены в таблице:
245. В институте 80 групп студентов (по 30 человек в каждой). Во всех группах проведена контрольная работа по математике. Сумма баллов, полученных каждой группой, дается в таблице: 246. Выход валовой продукции на 1 га с.х. угодий в (руб.) дается следующей таблицей (для нескольких хозяйств):
247. Исследователь, изучающий выработку на одного рабочего в % к предыдущему году, получил данные:
248. Имеются данные о дневном сборе клубники 50 колхозников (кг):
249. Контрольные обмеры диаметра валиков дали следующие результаты – приведены два десятичных знака после запятой, целая часть равна 7мм:
250. Контрольные обмеры диаметров шариков дали следующие результаты (указаны знаки после запятой) целая часть равна 5мм:
В задачах 251-260 по данным задачи надо реализовать схему однофакторного дисперсионного анализа.
251. Имеются результаты конкурсного сортоиспытания озимой пшеницы (урожайность в ц/га). Изучить влияние сорта на урожайность. Уровень значимости
252. На уровне значимости
253. На уровне значимости
254. На уровне значимости
255. На химическом заводе разработаны два новых варианта технологического процесса. Чтобы оценить, как изменится дневная производительность труда, завод в течение 5 дней работает по каждому варианту, включая существующий. Методом дисперсионного анализа на уровне значимости 0,01 исследовать влияние технологического процесса на дневную производительность завода (в условных единицах).
256. На заводе разработаны три варианта технологического процесса и в течение 5 дней завод работает по каждому процессу. На уровне значимости
257. Из группы полевых транзисторов взяты три выборки: в начале месяца, в середине и в конце. Выяснить на уровне значимости
258. На уровне значимости
259. Однотипные втулки обрабатывают на трех станках. Методом дисперсионного анализа исследовать зависимость диаметра этих втулок от типа станка. Уровень значимости
260. В таблице приведен вес (кг) поросят, родившихся в различных опоросах. Методом дисперсионного анализа исследовать зависимость веса от номера опороса. Уровень значимости
В задачах 261-270 методом линейного корреляционного анализа исследовать зависимость результирующего признака Y от факторного признака X.
261. Исследовать зависимость между количеством осадков в мае – августе Х (мм) и прибавкой урожая картофеля Y (ц/га)
262. Исследовать зависимость между длиной колоса озимой пшеницы Х (см) и числом зерен Y в колосе.
263. Исследовать зависимость между успехами в чтении (Х) и арифметики (Y) по данным таблицы, в которой представлены ряды оценок по тестам чтения и арифметики.
264. Исследовать зависимость выхода продукта Y (кг/час) от температуры реакции Х ( 0С) на некотором химическом производстве.
265. Исследовать зависимость издержек обращения Y (тыс. руб.) от величины розничного товарооборота магазинов Х (млн. руб.).
266. Исследовать зависимость выпуска продукции Y (тыс. руб.) от стоимости основных фондов Х (тыс. руб.).
267. Исследовать зависимость урожайности картофеля Y (ц/га) от уровня внесения органических удобрений Х (т/га).
268. Методом корреляционного анализа исследовать связь между средним доходом Х на семью (тыс. долларов) и разводов Y на 1000 жителей. Данные взяты в 9 штатах США.
269. Исследовать зависимость между производством Х (тыс. тонн) и ценой Y (дол.) вишни с 1960 по 1969г. (данные министерства сельского хозяйства США).
270. В таблице указаны уровни добычи угля в Англии (млн. тонн). Методом корреляционного анализа для первых 10 лет построить прямую регрессии. Последние три года использовать для сравнения прогноза с фактическим уровнем добычи.
Решение типовых примеров. Пример №1.(для задач 1-10). Вычислить определитель Решение. Напомним, что общий вид определителя третьего порядка следующий:
Числа аij, i =1, 2, 3; j =1, 2, 3, называются элементами определителя. Как видим, у всех элементов два индекса - первый индекс показывает номер строки, второй - номер столбца, на пересечении которых находится элемент. Обратим внимание на первую строку и в ней элемент а 12 , который равен единице. С помощью соответствующего свойства определителей все элементы второго столбца (кроме а 12=1) обратим в нули.
|

 и исправленную выборочную дисперсию
и исправленную выборочную дисперсию 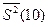 , сравнить полученные значения с соответствующими характеристиками генеральной совокупности;
, сравнить полученные значения с соответствующими характеристиками генеральной совокупности;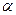 =0,05 при неизвестной и известной дисперсии;
=0,05 при неизвестной и известной дисперсии;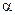 =0,05.
=0,05.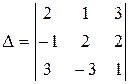 .
. .
.


