Моделі формування оптимального портфеля цінних паперів
Сучасна портфельна теорія (англ. modern portfolio theory, МРТ) була започаткована революційною роботою Гаррі Марковіца 1952 р.[2] Результати Марковіца були доповнені не менш відомими працями Джеймса Тобіна, Вільяма Шарпа та інших дослідників. Розглянемо задачу інвестора, який володіє капіталом W та має прийняти рішення, яким чином використати цей капітал. Припустимо, що інвестор розглядає фіксований плановий горизонт — кошти W необхідно розподілити на певний період. У інвестора є N можливостей використання коштів, кожна з яких принесе відповідно ξ1, ξ2,…,ξN гривень доходу в розрахунку на 1 гривню вкладень. Найбільш суттєвою проблемою для прийняття рішення є те, що величини ξ. загалом випадкові, тобто яким буде дохід наперед невідомо. Головним припущенням Марковіца, аналізуючи цю задачу, було таке, що для інвестора у оцінюванні альтернативних рішень важливими є тільки два параметри кожного з них: 1) очікувана дохідність інвестицій
де E — математичне очікування; 2) стандартне відхилення дохідності як показник, що характеризує ризик напряму інвестування:
де D — дисперсія. Це припущення в цілому не суперечить теорії очікуваної корисності Неймана- Моргенштерна: для того, щоб воно виконувалось, необхідно або розподілення доходностей активів ξi згідно з нормальним законом, або квадратична форма функції корисності багатства[3]. Друге, не менш важливе, припущення: інвестор не обов'язково повинен обрати якесь одне рішення, він може обрати будь-яку комбінацію можливих інвестицій, розподіляючи свої кошти за різними напрямками вкладень. При цьому проблема вибору значно спрощується. Нехай xi., і = 1, N, — це частка загального обсягу коштів, яка інвестується в і-й актив. Сформовану таким чином комбінацію інвестицій ми будемо називати портфелем. Інвестору необхідно обрати портфель з найкращими для нього очікуваною дохідністю Rp стандартним відхилення σp. Дохідність портфеля ξp, визначається як приріст коштів у розрахунку на одиницю вкладень, який забезпечується обраним портфелем на момент, визначений як плановий горизонт.
де W— сьогоднішній обсяг капіталу, WE — обсяг капіталу на кінець періоду.
Дохідність портфеля можна розрахувати як зважену за обсягами інвестицій дохідність кожного активу, що становлять портфель:
Очікувана дохідність портфеля визначається за формулою математичного очікування суми випадкових величин
Таким чином, очікувана дохідність інвестиційного портфеля — середньозважена за частками інвестицій очікувана дохідність кожного з активів, які становлять портфель. Дисперсія дохідності портфеля розраховується як дисперсія суми випадкових величин. Так, якщо ξ та η — випадкові величини,то
де Таким чином, для портфеля
позначимо
Отримаємо
Стандартне відхилення портфеля σp дорівнює
Модель поведінки інвестора, згідно з якою інвестиції оцінюють виключно за двома параметрами — очікуваною дохідністю і ризиком, що визначається як величина стандартного відхилення дохідності, дає змогу сформулювати єдине правило формування портфеля, яке виконують усі без винятку інвестори: незалежно від індивідуальних переваг, всі інвестори прагнуть сформувати ефективний портфель, який забезпечить мінімальний ступінь ризику для обраного рівня доходу чи максимальний очікуваний дохід при заданому ступені ризику. Цей підхід і сама задача вибору ефективного портфеля мають назву моделі Марковіца. Її завдання — визначити структуру найменш ризикованого портфеля при визначеному рівні доходності. Нехай xi — частка від суми інвестиції, яка буде використана на придбання і-го цінного папера. Тоді економіко-матема-тична модель Марковіца має вигляд:
Цільова функція моделі (1) є формалізацією ризику недосягнення заданого мінімального рівня дохідності, який мінімізується. Приклад (2) означає, що майбутня (очікувана) дохідність портфеля не повинна бути меншою, ніж деяке задане інвестором значення Rp. Формула (3) — вимога рівності всіх часток хi. одиниці. Зауважимо, що очікувана дохідність окремого і-го активу визначається як середнє значення у вибірці історичних даних. Модель можна подати в матричній формі, позначивши як х вектор розподілу коштів між ризиковими активами: х = {хi}i=1,….,N; R — вектор дохідності активів, V — коваріаційна матриця (квадратна матриця, що складається зі значень σij,
де е - одиничний вектор: всі елементи — одиниці; індекс Т означає транспонування вектора.
Для моделі можна знайти ров'язок в явному вигляді:
де
Як альтернатива до підходу мінімізації ризику за фіксованої дохідності є зворотний підхід: максимізувати дохідність при фіксуванні рівня ризику. Зважаючи на це, до задачі у класичній постановці (Марковіца) є обернена
Слід зазначити, що хоча теоретично цей підхід розглядається як альтернатива до першого, але він менш привабливий для практичного застосування. Для інвестора значно зрозуміліше і простіше визначити бажаний рівень дохідності (яка і є метою інвестування) і тоді за допомогою моделі мінімізувати ризик її недоотримання, ніж фіксувати розмір ризику, не знаючи чітко рівня дохідності, якого вдасться за визначеного ризику досягти. Модель Марковіца (1) - (3) була розвинена Джеймсом Тобіном для випадку наявності можливості здійснювати інвестиції в безризикові активи поряд з ризикованими. Отже, припустимо, що існує безризиковии актив з дохідністю R0, при цьому інвестор може вкласти в нього частку свого капіталу в обсязі х0. Безризиковий статус цього активу означає, що інвестор гарантовано за будь-яких умов отримає дохід від інвестицій в цей актив на рівні R0, тобто у цьому активі немає коливань дохідності. Тобто модель Тобіна можна записати у вигляді
Від обмеження (3) можна позбутися, зробивши заміну
Тоді обмеження (2) матиме вигляд
і розв'язок задачі записують у вигляді
До задачі Тобіна також можна записати обернену
|

 (16)
(16) (17)
(17) (18)
(18)
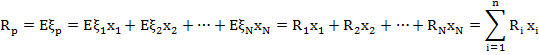
 ,
,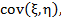 — коефіцієнт коваріації випадкових величин ξ та η.
— коефіцієнт коваріації випадкових величин ξ та η.
 ,
, 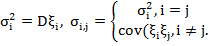


 (19)
(19) (20)
(20) (21)
(21) ):
):


 (4)
(4)

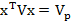

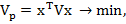



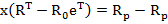
 (22)
(22)



