Мінімізація ризиків шляхом формування оптимального портфеля цінних паперів
Модель оцінки капітальних активів (МОКА) була вперше сформульована В. Шарпом в 1964 р.[1] та, незалежно від нього, Д. Літнером і Ж. Моссеном. Основні припущення моделі МОКА повторюють припущення портфельної теорії, перш за все, стосовно закономірностей формування індивідуальних інвестиційних рішень. Однак не менш суттєві і погляди щодо ринку в цілому. Основні припущення моделі такі: 1) інвестори оцінюють інвестиційні рішення за двома параметрами — очікуваною (середньою) дохідністю Ri. та величиною ризику, що визначається як стандартне відхилення випадкової величини дохідності σi; 2) немає податків і операційних витрат. Можливості короткого продажу необмежені, а його при цьому інтерпретують як продаж позиченого активу, маючи намір викупити в майбутньому за нижчою ціною; 3) існує безризикова ставка R0, однакова як для кредитів, так і для інвестицій. Можливості безризикового кредитування та інвестування необмежені; 4) активи підлягають нескінченному поділу; 5) усі інвестори не схильні до ризику й інвестують у більш ризиковані проекти тільки за умови, що вони забезпечують більший очікуваний дохід; 6) усі інвестори однаково інформовані щодо очікуваної дохідності та ризику інвестицій і мають однакові сподівання на майбутнє; 7) фінансові ринки досконало конкурентні — жоден з учасників не може здійснювати вплив на ціни, які визначаються виключно під впливом факторів ринкового попиту та пропозиції; 8) горизонт прийняття рішень однаковий для всіх інвесторів. У моделі МОКА рівноважна ціна (дохідність) окремого фінансового активу визначається суто ступенем статистичного взаємозв'язку дохідності цього активу і дохідності ринкового портфеля, який характеризується коефіцієнтом бета (βi.):
де Ri. — дохідність і-го фінансового активу; R0 — дохідність безризикового активу; Rт — дохідність ринкового портфеля (індексу); (Rт - R0) — премія за ризик; βi, — коефіцієнт пропорційності зміни дохідності і-го активу при зміні дохідності ринку. Коефіцієнт бета — це коефіцієнт коваріації дохідності фінансового активу і дохідності ринкового портфеля, поділеного на дисперсію дохідності ринкового портфеля:
де σi,m. — коефіцієнт коваріації ринкової дохідності та дохідності i-го фінансового активу; σ2т — стандартне відхилення дохідності ринкового портфеля (дисперсія). Таким чином, коефіцієнтом бета вимірюється чутливість дохідності i-го активу до коливань ринкової дохідності. Якщо βi. > 0 (що характерно для більшості активів), то при зниженні дохідності інвестицій на ринку в цілому знижується й дохідність певного цінного папера. При цьому, якщо βi > 1 — мінливість ціни (дохідності) цінного папера перевищує середньо ринковий рівень, що свідчить про більшу ризикованість, то і дохідність такого активу має бути більшою, ніж у середньому на ринку. У випадку βi. < 0, який трапляється рідше, статистична залежність дохідностей цінного папера та ринкового портфеля обернена. Такий актив може використовуватись для хеджування ризику, пов'язаного з інвестуванням у диверсифікований портфель фінансових активів.
|

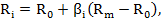 (14)
(14)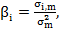 (15)
(15)


