Визначення ризику портфелю інвестицій
Портфель інвестицій – це набір фінансових активів, якими володіє інвестор. В нього можуть входити як інструменти одного виду, наприклад, акції або облігації, так і різні інструменти: цінні папери, фінансові інструменти, нерухомість. Головна мета формування портфелю інвестицій полягає в одержанні необхідного рівня очікуваної доходності при більш низькому рівні очікуваного ризику. Ця мета досягається за рахунок: по-перше, диверсифікації портфелю, тобто розподілу коштів інвестора між різними активами; по-друге, ретельного підбору фінансових інструментів. Розвиток широкого і ефективного ринку, статистичної бази, а також швидкий прогрес в області обчислювальної техніки призвели до виникнення сучасної теорії і практики управління портфелем фінансових інструментів. Вона побудована на використанні статистичних і математичних методів підбору фінансових інструментів в портфель, а також на ряді нових концептуальних підходів. Головними параметрами при управлінні портфелем є його очікувана доходність і ризик. При формуванні портфелю неможливо точно визначити майбутню динаміку його доходності і ризику. Дані величини спочатку оцінюються на підставі статистичних звітів за попередні періоди. Оскільки майбутнє навряд чи повторить минуле зі стовідсотковою ймовірністю, то одержані оцінки можуть бути скориговані згідно зі своїми очікуваннями розвитку майбутньої кон’юнктури. При аналізі доцільності операцій з портфелем цінних паперів, в тому числі тих, що впливають на його склад і структуру, можуть розв’язуватись три основні цільові задачі: а) досягнення максимально можливої доходності; б) досягнення мінімально можливого ризику; в) одержання деякого прийнятного значення комбінації “доходність/ризик”. Доходність портфелю визначається за формулою арифметичної середньозваженої. Тому задача максимізації доходності портфелю, у випадку її постановки, може бути вирішена однозначно і без особливих проблем, в тому числі і розрахункового характеру, оскільки об’єднання в портфель високоприбуткових активів забезпечує і високу доходність портфелю. Вирішення другої задачі є складнішим. Якщо мова йде про безризиковий портфель, то проблем не виникає, оскільки такий портфель може бути сформований, наприклад, із державних цінних паперів. Будь-які інші цільові настанови, пов’язані з мінімізацією ризику, в принципі здійснюються в рамках вирішення третьої задачі. Одержання деякого прийнятого значення комбінації “доходність/ризик” є переважаючим в інвестиційній діяльності. Це складне завдання і, як правило, не може мати однозначного вирішення. Якщо аналізується доцільність додаткового включення до портфелю одного активу, то задача оптимізації відносно нескладна і зводиться до аналізу наслідків об’єднання двох активів. Додавання в портфель декількох активів, рівнозначно як і будь-які інші комбінації, приводить до багатоваріантних в плані досягнення оптимального значення комбінацій “доходність/ризик”. Ризик портфелю, будучи нелінійною функцією, залежить від низки параметрів, основні з яких – кількість активів в портфелі, його структура та ризикованість його окремих складових і динаміка доходності. Поряд з цим, слід пам’ятати, що ризик портфелю залежить не від значень доходності, а від їх варіації та структури портфелю. Додавання в портфель безризикового активу зменшує доходність портфелю, при цьому ризик портфелю зменшується прямо пропорційно частці цього активу. Дійсно, оскільки
де: σnp – середнє квадратичне нового портфелю; σоp – середнє квадратичне старого портфелю; dnp – частка активів старого портфеля в новому. Об’єднання ризикових активів в портфель може призводити до зниження ризику в порівнянні з володінням кожним з цих активів окремо, однак результат залежить не тільки від ризикованості об’єднаних активів, але й від характеру взаємозв’язку між їх доходностями. Отже, ризик комбінації завжди менше максимального ризику об’єднаних активів. При об’єднанні в портфелі незалежних активів (в цьому випадку значення парних коефіцієнтів кореляції rij дорівнюють нулю) ризик портфелю може бути знайдений за формулою:
При включенні до портфелю ризикового активу, доходність якого змінюється в одному напрямку з доходністю портфелю і описується прямим функціональним зв’язком, ризик нової комбінації залишається без змін тільки в тому випадку, коли значення варіації доходності об’єднаних активу і портфеля є однаковими. Оскільки в реальному житті на ринку цінних паперів функціональні зв’язки можливі лише теоретично, то це означає, що розширення портфелю завжди супроводжується зміною його ризику. Якщо доходність активу, що планується включити до портфелю, змінюється в одному напрямку з доходністю портфелю та описується кореляційним зв’язком, то ризик нової комбінації може змінитися в будь-який бік в порівнянні з ризиком вихідного портфелю. Якщо до портфелю додається актив, доходність якого змінюється не в одному напрямі з доходністю портфелю, то ризик нової комбінації, як правило, зменшується. Якщо є на вибір два активи з однаковими характеристиками, однак доходність одного з них змінюється однонаправлено, а доходність другого – різнонаправлено з доходністю портфеля, то з позиції мінімізації ризику для включення їх до портфелю потрібно надати перевагу другому активу. Проблема оцінки вартості активів, головним чином, залежить від їх ризику та доходності. На ринку дотримується закономірність: чим вищий потенційний ризик, тим більшою повинна бути очікувана доходність. У кожного інвестора формуються свої прогнози відносно вищевказаних параметрів. В той же час ринок постійно змінюється в напрямку певної рівноважної оцінки ризику і доходності активів. Можливі розбіжності в оцінках, в першу чергу, пов’язані з асиметричністю інформації, якою володіють різні інвестори. В умовах добре розвиненого ринку нова інформація знаходить швидке відображення в курсовій вартості активів, тому для таких умов можна побудувати модель, яка б задовільно описувала взаємозв’язок між ризиком і очікуваною доходністю активів. Така модель була розроблена в середині 60-х рр. У. Шарпом і Дж. Лінтерном і одержала назву моделі оцінки вартості активів (capital asset pricing model – CAPМ). Як відомо, вартість активу визначається шляхом дисконтування майбутніх доходів, які він принесе, під відсоткову ставку, що відповідає його ризику. Проте, модель оцінки вартості активів не дає безпосередньої відповіді на питання, якою повинна бути ціна активу. Однак, вона одержала таку назву тому, що дозволяє визначити ставку дисконтування, яка використовується для розрахунку вартості фінансового інструменту. Модель має наступні обмеження, які одночасно визначають її недоліки: ̶ ринок є ефективним, тобто в курсовій вартості активу нова інформація відразу знаходить відображення; ̶ активи ліквідні і подільні, відсутні податки, трансакційні витрати, банкрутство; ̶ всі інвестори мають однакові очікування, діють раціонально, намагаючись максимізувати свою корисність, мають можливість брати кредит і надавати кошти під ставку без ризику; ̶ розглядається один часовий період; доходність є тільки функцією ризику; ̶ зміни цін активів не залежать від рівнів цін, що існували в минулому. В САРМ залежність між ризиком і очікуваною доходністю графічно можна описати за допомогою лінії ринку капіталу (Capital Market Line – CML), яка представлена на рис. 7.
Рис. 7. Лінія ринку капіталу CML є прямою лінією, рівняння якої можна представити наступним чином: y = a + bx, де: a – значення ординати в точці перетину її лінією CML, що відповідає ставці без ризику rf; b – кут нахилу CML. Кут нахилу визначається як відношення зміни значення функції до зміни аргументу. В нашому випадку (див рис. 7) кут нахилу дорівнює:
Оскільки очікувана доходність (у) є функція ризику (х), то у вже прийнятих термінах доходності і ризику рівняння CML буде мати вигляд:
де: σі – ризик і-го портфеля, для якого визначається рівень очікуваної доходності; E(ri) – очікувана доходність і-го портфеля. Дане рівняння можна записати наступним чином:
Очікувана доходність портфелю дорівнює ставці без ризику плюс добуток відношення ризику портфелю до ризику ринкового портфелю і різниці між очікуваною доходністю ринкового портфелю і ставкою без ризику. Приклад rf = 15 %, E(rm) = 30 %, σi =32 %, σm = 20 %. Визначити очікувану доходність портфеля. Вона дорівнює:
Всі можливі оптимальні (ефективні) портфелі, тобто портфелі, які включають в себе ринковий портфель М, розміщені на лінії rfL. Вона проходить через дві точки – rf і М. Таким чином, лінія ринку капіталу є дотичною до ефективної межі. Всі інші портфелі, в які не входить ринковий портфель, розміщуються нижче лінії rfL. CML піднімається вгору зліва направо і свідчить про те, що якщо портфель має більш високий ризик, то він повинен пропонувати інвестору більш високу очікувану доходність. Якщо вкладник бажає одержати більш високу очікувану доходність, він повинен погодитися на більш високий ризик. Нахил CML потрібно розглядати як винагороду (в одиницях очікуваної доходності) за кожну додаткову одиницю ризику, яку бере на себе вкладник. Коли вкладник купує актив без ризику, він забезпечує собі доходність на рівні ставки без ризику rf. Якщо він намагається одержати більш високу очікувану доходність, то повинен погодитися і на деякий ризик. Ставка без ризику є винагородою за час, тобто гроші в часі мають цінність. Додаткова доходність, що одержується інвестором понад ставки без ризику, є винагородою за ризик. Таким чином, винагорода особи, що інвестувала свої кошти в ринковий портфель, складається із ставки rf, яка є винагородою за час, і премії за ризик в розмірі E(rm) – rf. Іншими словами, на фінансовому ринку його учасники погоджують між собою ціну часу і ціну ризику. CML свідчить про співвідношення ризику і очікуваної доходності тільки для широко диверсифікованих портфелів, тобто портфелів, що включають ринковий портфель, але не відповідає на запитання, якою очікуваною доходністю повинні володіти менш диверсифіковані портфелі або окремі активи. Ринкові і неринкові ризики. Ефект диверсифікації. Як вже згадувалося вище, ризик, з яким пов’язане володіння активом, можна поділити на дві частини. Перша складова – це ринковий ризик. Його також називають системним або недиверсифікованим (неспецифічним). Він пов’язаний із станом кон’юнктури ринку, загальнозначущими подіями (війною, революцією тощо). Друга складова – неринковий, специфічний або диверсифікований ризик. Він пов’язаний з індивідуальними властивостями конкретного активу, а не зі станом ринку в цілому. Наприклад, власник будь-якої акції ризикує зазнати втрат в зв’язку із страйком на підприємстві, що випустило даний цінний папір, некомпетентністю його керівництва тощо. Цей ризик є диверсифікованим, оскільки його можна звести практично до нуля за допомогою диверсифікації портфелю. Як показали дослідження західних вчених, портфель, який складається з добре підібраних 10-20 активів, здатний фактично повністю виключити неринковий ризик (рис. 8).
Рис. 8. Ефект диверсифікації Широко диверсифікований портфель містить в собі тільки ринковий ризик. Недостатньо диверсифікований портфель володіє як ринковим, так і неринковим ризиками. Таким чином, інвестор може знизити свій ризик тільки до рівня ринкового, якщо формує широко диверсифікований портфель. Придбавши актив, вкладник розраховує одержати компенсацію за ризик, на який він йде. Однак ризик складається з двох частин. Яким же чином ринок оцінює компоненти ризику з точки зору очікуваної доходності? В рамках моделі САРМ розраховують на те, що вкладник може вільно купувати і продавати активи без додаткових витрат. Таким чином, без витрат інвестор здатний практично повністю виключити специфічний ризик за рахунок формування широко диверсифікованого. Тому в теорії вважається, що неринковий ризик не підлягає винагороді, оскільки він легко усувається диверсифікацією. Якщо інвестор не диверсифікує належним чином свій портфель, він йде на непотрібний ризик з точки зору тієї вигоди, яку він приносить суспільству. Придбавши, наприклад, акцію, інвестор фінансує виробництво і таким чином приносить суспільству користь. Купівля акції пов’язана з неринковим ризиком, який неможливо усунути. Тому інвестор повинен одержувати винагороду, адекватну тільки даному ризику. В протилежному випадку він не придбає цей папір. Однак суспільство (ринок) не буде винагороджувати його за специфічний ризик, оскільки він легко усувається диверсифікацією. З точки зору фінансування потреб економіки, цей ризик не має змісту. Таким чином, винагороді підлягає тільки системний ризик. Тому вартість активів повинна оцінюватись відносно величини саме цього ризику. Весь ризик активу (портфелю) вимірюється такими показниками, як дисперсія і стандартне відхилення. Для оцінки ринкового ризику застосовується інша величина, яку називають бета-коефіцієнт. Рівень ризику окремих цінних паперів визначається на основі наступних значень β-коефіцієнту: β = 1 – середній ризик; β > 1 – високий ризик; β < 1 – низький ризик. Таким чином, разом із зростанням значень β-коефіцієнту зростає і рівень систематичного ризику. β-коефіцієнт показує залежність між доходністю активу (портфелю) і доходністю ринку. Доходність ринку – це доходність ринкового портфелю. Оскільки неможливо сформувати портфель, в який би входили всі фінансові активи, то в якості нього приймається будь-який індекс з широкою базою. Тому доходність ринку – це доходність портфелю, представленого обраним індексом. Знаючи величину β для кожного з активів, вкладник може легко сформувати портфель необхідного рівня ризику та доходності. β портфелю – це середньозважене значення величин β активів, що входять в портфель, де вагою виступає їх частка в портфелі. Вона розраховується за формулою:
де: βp – бета портфелю; βі – бета і-го активу; θі – питома вага і-го активу. β кожного активу розраховується на підставі доходності активу і ринку за попередні періоди часу. Інформацію про значення β можна одержати від аналітичних компаній, які займаються аналізом фінансового ринку, а також з періодичної преси. β дозволяє оцінити ризик індивідуальної фінансової операції по відношенню до рівня ризику фінансового ринку в цілому. Цей показник використовується, в основному, для аналізу ризикованості вкладень в окремі цінні папери (в порівнянні зі систематичним ризиком всього фондового ринку). Розрахунок цього показника здійснюється за формулою:
де: β – значення бета-коефіцієнту; P – кореляція між доходом від індивідуального виду цінних паперів і середнім рівнем доходності фондових інструментів в цілому; σц – середньоквадратичне відхилення доходності від індивідуального виду цінних паперів; σф – середньоквадратичне відхилення доходності по фондовому ринку в цілому. Величина β активу (портфелю) без ризику дорівнює нулю, тому що нулю дорівнює коваріація доходності активу (портфелю) без ризику з доходністю ринкового портфелю. Величина β активу (портфелю) показує, наскільки його ризик більше або менше ризику ринкового портфелю. Активи з β більше одиниці є більш ризиковими, а з β менше одиниці – менш ризиковими, ніж ринковий портфель. Відносно величини β активи поділяють на агресивні і захисні. β агресивних активів більше одиниці, а захисних – менше одиниці. Якщо β активу дорівнює одиниці, то його ризик дорівнює ризику ринкового портфелю. Величина β може бути як плюсовою, так і від’ємною. Плюсове значення β свідчить про те, що доходності активу (портфелю) і ринку при зміні кон’юнктури змінюються в одному напрямку. Від’ємна β показує, що доходності активу (портфелю) і ринку змінюються в протилежних напрямках. β активу (портфелю) показує, в якій мірі доходність активу (і відповідно його ціна) буде реагувати на дію ринкових сил. Знаючи β конкретного активу (портфелю), можна оцінити, наскільки повинна змінитися його очікувана доходність при зміні очікуваної доходності ринку. Наприклад, β цінного паперу дорівнює +2. Це означає, що при збільшенні очікуваної доходності ринкового портфелю на 1 % доходність цінного паперу зросте на 2 %, і навпаки, при зменшенні доходності ринкового портфелю на 1 % доходність цінного паперу знизиться на 2 %. Оскільки β цінного паперу більше одиниці, то вона є більш ризиковою, ніж ринковий портфель. Якщо β цінного паперу дорівнює 0,5, то при збільшенні очікуваної доходності ринку на 1 % очікувана доходність паперу повинна зрости тільки на 0,5 %. І навпаки, при зниженні доходності ринку на 1 % доходність цінного паперу зменшиться тільки на 0,5 %. Таким чином, ризик даного цінного паперу менше ризику ринку. Якщо β дорівнює -2, то при підвищенні доходності ринкового портфелю на 1 % доходність активу зменшиться на 2 % і, навпаки. Активи з від’ємною β є цінними інструментами для диверсифікації портфелю, оскільки в даному випадку можна побудувати портфель з “нульовою β ”, який не буде ризиковим. Однак потрібно пам’ятати, що такий портфель не аналогічний активу без ризику, так як при нульовому значенні β він не містить тільки систематичного ризику. В той же час даний портфель збереже неринковий ризик. Лінія ринку активу. CML показує співвідношення ризику і доходності для ефективних портфелів, але нічого не говорить про те, як будуть оцінюватися неефективні портфелі або окремі активи. На це питання відповідає лінія ринку активу (Security Market Line – SML) (рис. 9).
Рис. 9. Лінія ринку активу SML є головним підсумком САРМ. Вона говорить про те, що в стані рівноваги очікувана доходність активу дорівнює ставці без ризику плюс винагорода за ринковий ризик, який вимірюється величиною β. Вона представляє собою пряму лінію, що проходить через дві точки, координати яких дорівнюють rf; 0 і E(rm). Таким чином, знаючи ставку без ризику і очікувану доходність ринкового портфелю, можна побудувати SML. В стані рівноваги ринку очікувана доходність кожного активу і портфелю, незалежно від того, ефективний він чи ні, повинна розміщуватися на SML. Необхідно ще раз підкреслити, що якщо на CML знаходяться тільки ефективні портфелі, то на SML розміщуються як широко диверсифіковані, так і неефективні портфелі і окремі активи. Очікувану доходність активу (портфелю) визначають за допомогою рівняння SML
Якщо у інвесторів змінюються очікування відносно ставки без ризику, це призведе до зміщення SML. При збільшенні rf SML зміститься вгору, при зниженні – донизу (див. рис. 10 і 11). Отже, нахил SML визначається ставленням інвесторів до ризику в різноманітних умовах ринкової кон’юнктури. Якщо у вкладників оптимістичні прогнози на майбутнє, то нахил SML буде менш крутий, так як в умовах позитивної кон’юнктури інвестори згодні на більш високі ризики (оскільки вони менш ймовірні) при менших значеннях очікуваної доходності. Навпаки, в умовах несприятливої кон’юнктури SML набуде крутого нахилу, так як в даному випадку інвестори у вигляді компенсації будуть вимагати більш високої очікуваної доходності на активи, які придбають, для тих же значень ризику.
|

 за визначенням, то
за визначенням, то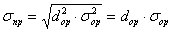 , (6)
, (6) (7)
(7)
 (8)
(8) , (9)
, (9) (10)
(10)

 , (11)
, (11) , (12)
, (12)
 . (13)
. (13)



