Явление конденсации указывает на притяжение молекул друг к другу. Этот факт каким-то образом должен быть отражен в уравнении состояния. Заметим, что силы притяжения молекул препятствуют их разлету. Это должно уменьшать давление газа по сравнению с предсказанием модели идеального газа. Обозначим это уменьшение через DP. Тогда выражение для давления с учетом уже сделанной объемной поправки будет иметь вид
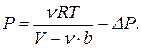 (5)
(5)
Оценим поправку DP имея в виду механизм создания молекулами газа давления на стенку. На подлетающую к стенке молекулу действуют силы притяжения к остальным молекулам газа, направленные вглубь сосуда и уменьшающие скорость молекулы. Приближенно можно считать, что эти силы должны быть пропорциональны плотности газа (чем больше молекул тянет назад, тем больше силы). Эти силы уменьшают передаваемый каждой молекулой импульс стенке. А так как передаваемый стенке импульс также пропорционален концентрации молекул, в итоге получаем
DP~n2 или  (6)
(6)
где a – постоянный для данного газа коэффициент. Таким образом, получаем следующее уравнение для давления
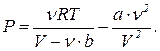 (7)
(7)
Это уравнение обычно записывают в виде
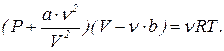 (8)
(8)
| Вещество
| a, H×м4×моль-2
| b, м3×моль-1
|
| Вода H2O
| 0,5464
| 0,305×10-4
|
| Азот N2
| 0,139
| 0,391×10-4
|
| Кислород O2
| 0,137
| 0,318×10-4
|
| Водород H2
| 0,0244
| 0,266×10-4
|
| Углек. газ CO2
| 0,367
| 0,43×10-4
|
Это – знаменитое уравнение Ван-дер-Ваальса, впервые опубликованное в 1873 году, за которое в 1910 году автор получил Нобелевскую премию.
У каждого газа свои поправки в уравнении состояния, то есть свои значения постоянных а и b. Для примера приведена таблица значений этих постоянных.
В отличие от идеального газа уравнение Ван-дер-Ваальса не является универсальным. Уравнение, допустим для одного моля гелия, отличается от уравнения для одного моля азота. Однако для любого газа можно подобрать такие единицы измерения объема – V0, давления – P0 и температуры – T0, что в новых переменных уравнения состояния любого газа будут одинаковыми. Найдем формулы для определения этих единиц
Пусть V=V0u, P=P0p, T=T0t. Подставим эти выражения в уравнение (8) для одного моля газа, разрешенное относительно P. Тогда
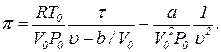 (9)
(9)
Чтобы уравнение приобрело универсальный и, по возможности, простой вид потребуем, чтобы
V0=b, 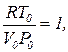
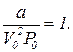 (10)
(10)
Из этих уравнений следует
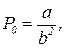 (11)
(11)
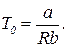 (12)
(12)
Соответственно уравнение Ван-дер-Ваальса принимает вид
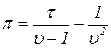
 или
или 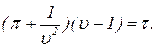 (13)
(13)
 Из уравнения состояния Ван-дер-Ваальса следует, что вид изотерм может значительно отличаться от изотерм идеального газа. В некоторой области температур на изотермах возникает складка. На рисунке изображено семейство изотерм одного моля газа. Участок изотермы AB в области складки имеет положительный наклон. Точки на этом участке изображают состояния, обладающие замечательными свойствами. Предположим, однородный газ находится в одном из таких состояний. Мысленно разделим все количество газа на две половинки. Каждая из половинок действует на соседку с давлением P. Вследствие тепловых
Из уравнения состояния Ван-дер-Ваальса следует, что вид изотерм может значительно отличаться от изотерм идеального газа. В некоторой области температур на изотермах возникает складка. На рисунке изображено семейство изотерм одного моля газа. Участок изотермы AB в области складки имеет положительный наклон. Точки на этом участке изображают состояния, обладающие замечательными свойствами. Предположим, однородный газ находится в одном из таких состояний. Мысленно разделим все количество газа на две половинки. Каждая из половинок действует на соседку с давлением P. Вследствие тепловых
 флуктуаций объемы порций слегка колеблются. В соответствии с уравнением состояния как угодно малое увеличение объема приведет к увеличению давления в этой половинке, а в сжавшейся – к понижению. Так что одна половинка будет неудержимо расширяться, а другая сжиматься. Это означает, что однородное состояние газа на данном участке является неустойчивым. Газ должен расслаиваться на части неравной плотности. Это явление – ничто иное, как конденсация – расслоение на две фазы.
флуктуаций объемы порций слегка колеблются. В соответствии с уравнением состояния как угодно малое увеличение объема приведет к увеличению давления в этой половинке, а в сжавшейся – к понижению. Так что одна половинка будет неудержимо расширяться, а другая сжиматься. Это означает, что однородное состояние газа на данном участке является неустойчивым. Газ должен расслаиваться на части неравной плотности. Это явление – ничто иное, как конденсация – расслоение на две фазы.
Из проведенного рассуждения следует, что уравнение Ван-дер-Ваальса предсказывает конденсацию газа, чего не было в модели идеального газа.
Экспериментальная изотерма в обсуждаемой области имеет не складку, а плато (на рисунке выделено жирным). Уровень, по которому проходит плато разрезает складку так, что площади между уровнем и изотермой Ван-дер-Ваальса, проходящей сверху и снизу уровня, (на рисунке площади заштрихованы) равны.
Заметим, что с повышением температуры изотерм область складки становится уже.Наконец, на некоторой перегиб сливается с точкой экстремума. Складка исчезает. Расслоение на фазы невозможно. Точка перегиба описывает критическое состояние (при температурах ниже критической газ можно сжижить, а при температуре выше критической газ не сжижается).
Определим критическую температуру. Она определится из уравнений
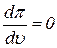 и
и 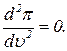 (14)
(14)
Используя уравнение (13), получим
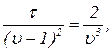 (15)
(15)
 (16)
(16)
Поделив почленно (15) на (16), найдем объем, который занимает моль газа в критическом состоянии:
uк=3 (17)
Подстановка полученного значения в любое из уравнений дает
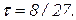 (18)
(18)
Таким образом, при проведении обезразмеривания уравнения Ван-дер-Ваальса более физичным является следующее определение безразмерных параметров состояния:
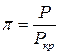 , где
, где 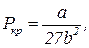 (19)
(19)
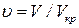 , где Vкр=3b (20)
, где Vкр=3b (20)
 , где
, где  (21)
(21)
В этих переменных уравнение состояния любого газа имеет вид
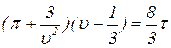 . (22)
. (22)
Это уравнение называется приведенным уравнением Ван-дер-Ваальса.
Изотермы на приведенном выше рисунке изображены именно в этих переменных. При построении кривых обнаруживается, что при безразмерных температурах меньших 0,84 в некотором интервале значений объема давление становится отрицательным, что является нефизичным предсказанием. Поэтому мы должны сделать вывод, что так же как и уравнение состояния идеального газа, уравнение Ван-дер-Ваальса является приближенным и не годится при больших плотностях и низких температурах.

 В заключение отметим еще одно обстоятельство. Наличие притяжения между молекулами не достаточно для конденсации. При потенциальном взаимодействии сближаясь, молекулы ускоряются. Понижение потенциальной идет на увеличение кинетической энергии. Так что связанное состояние двух или более молекул так просто не может возникнуть. Слипание произойдет только в том случае, когда излишек кинетической энергии при сближении молекул будет передан третьей или пойдет на возбуждение внутренних степеней свободы молекулы (см. рисунок 70).
В заключение отметим еще одно обстоятельство. Наличие притяжения между молекулами не достаточно для конденсации. При потенциальном взаимодействии сближаясь, молекулы ускоряются. Понижение потенциальной идет на увеличение кинетической энергии. Так что связанное состояние двух или более молекул так просто не может возникнуть. Слипание произойдет только в том случае, когда излишек кинетической энергии при сближении молекул будет передан третьей или пойдет на возбуждение внутренних степеней свободы молекулы (см. рисунок 70).

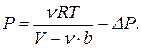 (5)
(5)  (6)
(6) 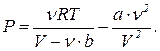 (7)
(7)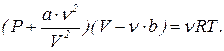 (8)
(8)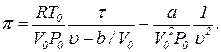 (9)
(9) 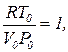
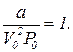 (10)
(10) 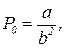 (11)
(11) 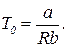 (12)
(12) 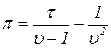
 или
или 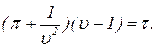 (13)
(13) Из уравнения состояния Ван-дер-Ваальса следует, что вид изотерм может значительно отличаться от изотерм идеального газа. В некоторой области температур на изотермах возникает складка. На рисунке изображено семейство изотерм одного моля газа. Участок изотермы AB в области складки имеет положительный наклон. Точки на этом участке изображают состояния, обладающие замечательными свойствами. Предположим, однородный газ находится в одном из таких состояний. Мысленно разделим все количество газа на две половинки. Каждая из половинок действует на соседку с давлением P. Вследствие тепловых
Из уравнения состояния Ван-дер-Ваальса следует, что вид изотерм может значительно отличаться от изотерм идеального газа. В некоторой области температур на изотермах возникает складка. На рисунке изображено семейство изотерм одного моля газа. Участок изотермы AB в области складки имеет положительный наклон. Точки на этом участке изображают состояния, обладающие замечательными свойствами. Предположим, однородный газ находится в одном из таких состояний. Мысленно разделим все количество газа на две половинки. Каждая из половинок действует на соседку с давлением P. Вследствие тепловых флуктуаций объемы порций слегка колеблются. В соответствии с уравнением состояния как угодно малое увеличение объема приведет к увеличению давления в этой половинке, а в сжавшейся – к понижению. Так что одна половинка будет неудержимо расширяться, а другая сжиматься. Это означает, что однородное состояние газа на данном участке является неустойчивым. Газ должен расслаиваться на части неравной плотности. Это явление – ничто иное, как конденсация – расслоение на две фазы.
флуктуаций объемы порций слегка колеблются. В соответствии с уравнением состояния как угодно малое увеличение объема приведет к увеличению давления в этой половинке, а в сжавшейся – к понижению. Так что одна половинка будет неудержимо расширяться, а другая сжиматься. Это означает, что однородное состояние газа на данном участке является неустойчивым. Газ должен расслаиваться на части неравной плотности. Это явление – ничто иное, как конденсация – расслоение на две фазы.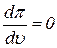 и
и 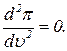 (14)
(14) 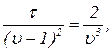 (15)
(15)  (16)
(16) 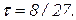 (18)
(18)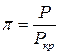 , где
, где 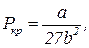 (19)
(19)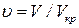 , где Vкр=3b (20)
, где Vкр=3b (20) , где
, где  (21)
(21) 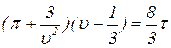 . (22)
. (22) 
 В заключение отметим еще одно обстоятельство. Наличие притяжения между молекулами не достаточно для конденсации. При потенциальном взаимодействии сближаясь, молекулы ускоряются. Понижение потенциальной идет на увеличение кинетической энергии. Так что связанное состояние двух или более молекул так просто не может возникнуть. Слипание произойдет только в том случае, когда излишек кинетической энергии при сближении молекул будет передан третьей или пойдет на возбуждение внутренних степеней свободы молекулы (см. рисунок 70).
В заключение отметим еще одно обстоятельство. Наличие притяжения между молекулами не достаточно для конденсации. При потенциальном взаимодействии сближаясь, молекулы ускоряются. Понижение потенциальной идет на увеличение кинетической энергии. Так что связанное состояние двух или более молекул так просто не может возникнуть. Слипание произойдет только в том случае, когда излишек кинетической энергии при сближении молекул будет передан третьей или пойдет на возбуждение внутренних степеней свободы молекулы (см. рисунок 70).


