Капиллярные явления. Поверхность жидкости, налитой в сосуд, вблизи стенок искривлена
Поверхность жидкости, налитой в сосуд, вблизи стенок искривлена. Это происходит там, где заметную роль играют силы взаимодействия между молекулами жидкости и твердого тела. Если размеры свободной межфазной поверхности сравнимы с радиусом кривизны, то основным фактором, определяющим форму поверхности, является поверхностное натяжение. Явления, происходящие в сосудах или иных вместилищах жидкости с малыми размерами свободной поверхности, называются капиллярными явлениями. Так как для капиллярных сосудов характерна кривизна свободной поверхности, определяющую роль в равновесии жидкости играет лапласовское давление. Одно из явлений подобного рода – капиллярный подъем.
Условие равновесия – Учтем, что если r – радиус капилляра, то
|
На рисунке изображена узкая трубка, опущенная в широкий сосуд с жидкостью. Добавочное давление, обусловленное кривизной поверхности жидкости направлено к центру кривизны мениска и равно 2s23/r*, где r* – радиус кривизны мениска. Под действием этого давления жидкость поднимается вверх по трубке до высоты h, при которой сумма добавочного и гидростатического давлений на уровне свободной поверхности в сосуде не станет равной нулю.
(12) 
Поэтому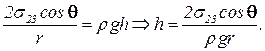 
(13) 
(14)
