Работа различных процессов
Под названием работы объединяются многие энергетические процессы; общим свойством этих процессов является затрата энергии системы на преодоление силы, действующей извне. К таким процессам относится, например, перемещение масс в потенциальном поле. Если движение происходит против градиента силы, то система затрачивает энергию в форме работы; величина работы положительна. При движении по градиенту силы система получает энергию в форме работы извне; величина работы отрицательна. Такова работа поднятия известной массы в поле тяготения. Элементарная работа в этом случае: d W = – mgdH где m – масса тела; H – высота над начальным нулевым уровнем. При расширении системы, на которую действует внешнее давление P, система совершает работу При движении электрического заряда q в электрическом поле против направления падения потенциала j и на участке, где изменение потенциала равно dj, а также при увеличении заряда тела, имеющего потенциал j, на величину dq работа совершается над системой, величина ее равна в первом случае – qdj, а во втором случае – jdq. Аналогичным образом можно выразить работу увеличения поверхности раздела S между однородными частями системы (фазами): d W = -s dS, В общем случае элементарная работа dW является суммой нескольких качественно различных элементарных работ: d W = Pd V – mgdH – s dS – j d q + … (1,12) Здесь P, -mg, - σ, -j – силы в обобщенном смысле (обобщенные силы) или факторы интенсивности; V, H, S, q – обобщенные координаты или факторы емкости. В каждом конкретном случае следует определить, какие виды работы возможны в исследуемой системе, и, составив соответствующие выражения для dW, использовать их в уравнении (I, 2а). Интегрирование уравнения (I, 12) и подсчет работы для конкретного процесса возможны только в тех случаях, когда процесс равновесен и известно уравнение состояния. Для очень многих систем можно ограничить ряд уравнения (I, 12) одним членом – работой расширения. Работа расширения при равновесных процессах выражается различными уравнениями, вытекающими из уравнения состояния. Приведем некоторые из них: 1) Процесс, протекающий при постоянном объёме (изохорный процесс; V = const): W = ∫δW = ∫PdV = 0 (I, 13) 2) Процесс, протекающий при постоянном давлении (изобарный процесс; P = const): W = 3) Процесс, протекающий при постоянной температуре (изотермический процесс, T = const). Работа расширения идеального газа, для которого PV = nRT: W =
|

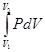 , элементарная работа равна в этом случае PdV (V1 и V2 – начальный и конечный объёмы системы соответственно).
, элементарная работа равна в этом случае PdV (V1 и V2 – начальный и конечный объёмы системы соответственно).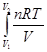 dV = nRT ln
dV = nRT ln 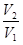 (I, 15)
(I, 15)


