Фазовые переходы. Уравнение Клапейрона-Клаузиуса
В системе, состоящей из нескольких фаз чистого вещества, находящихся в равновесии, возможны переходы вещества из одной фазы в другую. Такие переходы называются фазовыми переходами или превращениями агрегатных состояний. Рассмотрим равновесный переход одного моля вещества из одной фазы (1) в другую (2), совершающийся при постоянных давлении и температуре. Энергии Гиббса (G 1и G 2) моля вещества в фазах 1 и 2 равны (условие равновесия). Следовательно: G 2 = G 1 (III, 14) Напишем уравнения (III, 13б) полных дифференциалов для энергии Гиббса одного моля чистого вещества в двух равновесных фазах 1 и 2: dG1 = V1dP – S1dT dG2 = V2dP – S2dT (III, 15) Вычитая верхнее уравнение из нижнего, получим: dG 2 – dG 1 = (V 2 – V 1) dP – (S 2 – S 1) dT Изменения P и Т здесь были не независимыми, а такими, при которых сохранялось равновесие между фазами 1 и 2. Таким образом, между P и Т сохранялась функциональная связь, соответствующая фазовому равновесию. Поэтому, если G1 = G2 (равновесие при давлении P и температуре Т), то G 1 + dG 1 = G 2 + dG 2(равновесие при давлении P + dP и температуре T + dT), т. е. dG l = dG 2 или dG 2 – dG 1 = 0. Следовательно (V 2 – V 1) dP – (S 2 – S 1) dT = 0 или
Взаимное превращение, фаз рассматривалось здесь как равновесное и изотермическое, поэтому: S2 – S1 = DS = Здесь Из уравнений (III, 16) и (III, 17) получим:
Уравнение (III, 18) называется уравнением Клапейрона - Клаузиуса и является общим термодинамическим уравнением, приложимым ко всем фазовым переходам чистых веществ, т.е. к превращениям агрегатных состояний. При превращении одной фазы в другую такие свойства как удельный или мольный объём, внутренняя энергия и энтропия одного грамма или одного моля вещества изменяются скачкообразно. Однако отсюда не следует, что внутренняя энергия всей двухфазной системы не является в этом случае непрерывной функцией её состояния. В самом деле, система, состоявшая в начале процесса, например, из некоторого количества льда при 0°С и 1 атм, при постоянном давлении и подведении теплоты превращается в двухфазную систему лед-жидкая вода, в которой по мере поглощения теплоты масса льда постепенно и непрерывно убывает, а масса воды растет. Поэтому также постепенно и непрерывно изменяются такие свойства системы в целом как внутренняя энергия, энтальпия, энтропия и др.
|

 (III, 16)
(III, 16)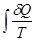 =
=  =
= 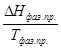 (III, 17)
(III, 17) – теплота фазового превращения, поглощаемая при переходе моля вещества из фазы 1 в фазу 2; V 2 – V 1 – разность мольных объёмов двух фаз.
– теплота фазового превращения, поглощаемая при переходе моля вещества из фазы 1 в фазу 2; V 2 – V 1 – разность мольных объёмов двух фаз. (III, 18)
(III, 18)


