| Объединенная классификация простых категорических суждений по количеству и качеству
| |
|
Формула
суждения
|
Обозна-чение
| Распреде-лённость терминов
| Графическое изображение
|
Словесное
пояснение
| |
|
1-й
вариант
|
2-й
вариант
| |
| |
| S
| P
| |
|
Все S
есть P
|
А
|
+
|
_
+
| 
| 
| Общеутвердительное – общее по количеству и утвердительное по качеству. Предикат приписывается всему субъекту.
| |
|
Ни одно S
не есть P
|
Е
|
+
|
+
| 
|
| Общеотрицательное – общее по количеству и отрицательное по качеству. Предикат отрицается во всём субъекте.
| |
|
Некоторые S
есть P
|
I
|
-
|
_
+
|
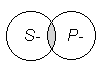
| 
| Частноутвердительное – частное по количеству и утвердительное по качеству. Предикат приписывается части субъекта.
| |
|
Некоторые S
не есть P
|
O
|
-
|
+
| 
| 
| Частноотрицательное – частное по количеству и отрицательное по качеству. Предикат отрицается в части субъекта.
| |
| Примечание: «+» - термин распределён; «-» - термин не распределён
| |
| Таблица5
Непосредственные умозаключения
| |
| Превращение
| Все S есть Р → Ни одно S не есть не Р.
Ни одно S не есть Р → Все S есть не Р.
Некоторые S есть Р → Некоторые S не есть не Р.
Некоторые S не есть Р → Некоторые S есть не Р.
| A→E
E→A
I→O
O→I
| 
| Превращение представляет собой изменение качества суждений. Связка меняется на противоположную, а предикат заменяется противоречащим ему понятием.
| |
| Обращение
без ограничений
| Все S есть Р → Все Р есть S.
Ни одно S не есть Р → Ни одно Р не есть S.
Некоторые S есть Р → Некоторые Р есть S.
| A→A
E→E
I→I
|

| При обращении предикат
посылки становится субъектом вывода, а субъект посылки – предикатом вывода.
Качество суждения при этом
не меняется. Обращение верно, если термин, не распределённый в посылке, не будет распределён и в выводе.
| |
| Обращение с
ограничением
| Все S есть Р → Некоторые Р есть S.
Некоторые S есть Р → Все Р есть S.
| A→I
I→A
| 
| |
| Частноотрицательные суждения не обращаются
| |
| Противопоставление
предикату
| Все S есть Р → Ни одно не Р не есть S.
Ни одно S не есть Р → Некоторые не Р есть S.
Некоторые S не есть Р → Некоторые не Р есть S.
| A→E
E→I
O→I
|

| Противопоставлением предикату называется изменение суждения, в результате которого субъектом становится понятие, противоречащее предикату, а предикатом – субъект исходного суждения.
| |
| Частноутвердительные суждения не противопоставляются предикату
| |
| Таблица 6
Фигуры простого категорического силлогизма
| | |
| M P
S M
S P
| P M
S M
S P
| M P
M S
S P
| P M
M S
S P
| | |
| Первая фигура
| Вторая фигура
| Третья фигура
| Четвёртая фигура
| | |
| Модусы простого категорического силлогизма
| | |
| EIO
EAE
AII
AAA
| EIO
EAE
AEE
AOO
| EIO
EAO
AII
AAI
IAI
OAO
| EIO
EAO
AEE
AAI
IAI
| | |
| Правила фигур
| | |
| 1. Большая посылка – общее суждение
2. Меньшая посылка – утвердительное суждение
| 1. Большая посылка – общее суждение
2. Одна из посылок – отрицательное суждение
| 1. Меньшая посылка – утвердительное суждение
2. Заключение – частное
суждение
|
| | |
| Общие правила простого категорического силлогизма
| | |
| 1. Должно быть только три термина.
2. Средний термин должен быть распределён хотя бы в одной посылке.
3. Термин, не распределённый в посылке, не распределен
и в заключении.
4. Одна посылка должна быть утвердительным суждением.
5. Если одна из посылок – отрицательное суждение, то и заключение – отрицательное суждение.
|
6. Одна из посылок должна быть общим суждением.
7. Если одна из посылок – частное суждение, то и
заключение – частное суждение.
8. Из двух утвердительных посылок нельзя получить
отрицательное заключение.
9. Если большая посылка – частное суждение, а
меньшая – отрицательное суждение, то вывод невозможен.
| | |
| | | | | | | | | | | | | | | | | | | |