Интуитивно-этический экстраверт, Инициатор, Гексли

 

Первый ряд ИЭЭ, который мы видим (401—403), — подтип, который иногда бывает трудно идентифицировать как Гексли. Возможно, это связано с тем, что их лица довольно спокойны, в них нет особой игривости, которая характерна для интуитивного подтипа. Возможно, этот подтип тот же, к которому принадлежит наш известный и всеми любимый кинодраматург и кинорежиссер Э. А. Рязанов. Его склонность к фантазиям настолько очевидна в фильмах, что интуитивность Э. А. Рязанова не вызывает никаких сомнений. И паровозы у него по небу летают, и машины въезжают в метро, и герой встречается сам с собой молодым... Лица этих людей довольно широкие, комплекция, как правило, плотная. Обратите внимание, что у интуитов могут оказаться и полные губы.

 

 

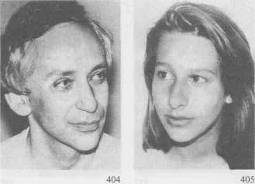
О подтипе пары второго ряда (404—405) мы уже говорили раньше. Этот подтип довольно часто встречается в жизни: удлиненные лица, соответственно лицу удлиненные, слегка выпуклые носы, достаточно явно выраженные скулы, полные губы. Эти люди, несмотря на большую разницу в возрасте, разный пол и разную национальность — похожи так, как будто перед нами отец и дочь.

 

 

Принадлежность следующей пары 406—407 к психотипу ИЭЭ настолько очевидна, что не вызывает никаких затруднений в определении. Достаточно взглянуть на их лукавые, шаловливые улыбки, и все становится сразу ясным.

 

 

Молодые люди (408—409) так похожи, что автору пришлось специально подробно рассматривать детали их лиц. Такое впечатление, что их посадили перед фотокамерой и попросили смотреть в одну точку. А между прочим, эти фотографии разных молодых людей отделяет несколько лет. Автор никогда не ограничивала свои модели определенным положением, просила только повернуться по-разному, чтобы получилось три-пять ракурсов. По-видимому, здесь мы встречаемся с абсолютно идентичными физиологическими проявлениями подтипа. Похоже, что к этому подтипу ИЭЭ принадлежал известный и любимый всеми киноартист А. Миронов.

 

 

Девушки (410—411) также очень типичны для этого психотипа — мягкие улыбки, не очень сильная демонстративность — по-видимому, это слегка интровертный этический подтип Гексли.

 

 

Последняя пара ближе всего по внешнему виду к паре во втором ряду, хотя есть и отличия. Верхняя часть головы у них сужается, эмоциональность, активность и сильная творческая жилка, вместе с некоторой игривостью взгляда — все это характеризует интуитивный подтип ИЭЭ.