СТАТИЧЕСКИЙ РАСЧЕТ БАЛКИ

Расчет балки с волнистой стенкой аналогичен расчету составной балки на податливых связях. Роль податливых связей играет стенка, которая не способна воспринимать нормальные напряжения. Нормальные напряжения воспринимаются поясами. Проверку нормальных напряжений в растянутом поясе производим по формуле:

σ_р = М/W_расч. = М/(k_wW_нт) ≤ R_р/γ_n,

где W_нт= 2I_х/h₀;

I_х = 2[bh³_n/12 + F_n(h₀/2)²];

h₀ = h - h _n;

F_n= b∙ h _n;

h₀ – высота между осями поясов,

h _n- высота пояса,

k_w – коэффициент снижения момента сопротивления поперечного сечения балки, вследствие податливости фанерной стенки, определяемый по формуле: k_w = 1/(1 + (b _n/h)В),

В – коэффициент податливости фанерной стенки, вычисляемый по формуле: В = π²Е_дS/(G_фℓ²δ),

ℓ - пролет балки,

δ – толщина стенки,

Е_д – модуль упругости материала поясов, для древесины ели или сосны Е_д =10000 МПа,

G_ф – модуль сдвига фанеры стенки, определяемый для фанеры марки ФСФ по таблице 11 СНиП II-25-80;

S – статический момент пояса шириной b и высотой h_п относительно нейтральной оси, вычисляемый по формуле: S = b∙h_п∙ h₀/2;

γ_n – коэффициент надежности по назначению, равный для зданий II класса ответственности 0,95.

Расчетный изгибающий момент в середине пролета балки:

М = q_р∙ℓ²/8 = 4,63∙6,3 ²/8 = 22,97 кНм.

Момент инерции поперечного сечения балки без учета фанерной стенки:

I_х = 2[23∙9.9³/12 + 23∙9.9(90.1/2)²] = 927955 см⁴.

W_нт= 2I_х/h₀ = 2∙927955/90,1 = 20598 см³.

S = b∙h_п∙ h₀/2 = 23∙9,9∙90,1/2 = 10258 см³.

В = 3,14²∙10000∙10258/(750∙880²∙1,8) = 0,97.

k_w = 1/(1 + (9,9/100)0,97) = 0,912.

σ_р = 10^-2∙2297000/(0,912∙20598) = 0,12 < R_р/γ_n,= 9/0,95 = 9,47 МПа.

Условие прочности выполняется.

Прогиб балки с волнистой стенкой определяем по формуле (50) СНиП II-25-80:

,

где f _о – прогиб балки постоянного сечения высотой h без учета деформаций сдвига;

h – высота сечения;

l – пролет балки;

k – коэффициент, учитывающий влияние переменности высоты сечения, принимаемый равным 1 для балок постоянного сечения;

с – коэффициент, учитывающий влияние деформаций сдвига от поперечной силы.

Значения коэффициентов k и с для основных расчетных схем балок определяем по табл. 3 прил. 4 СНиП II-25-80.

Прогиб балки f _о без учета деформаций сдвига определим по формуле:

,

Где k_ж – коэффициент снижения момента инерции поперечного сечения балки (определяемого без учета фанерной стенки), вследствие податливости фанерной стенки и вычисляемый по формуле:

k_ж = 1/(1 + В);

0,7 – поправочный коэффициент к жесткости ЕI_х поперечного сечения клеефанерной балки с волнистой стенкой, вводимый в расчет согласно п. 3.34 [7].

k_ж = 1/(1 + 0,97) = 0,51;

 

с = (45,3 - 6,9β)γ,

где β =1, табл. 3 прил. 4, СНиП II-25-80,

γ – отношение площади поясов к площади стенки (высотой h₀) клеефанерной балки.

γ = 2∙9,9∙23,0/(1,8∙90,1) = 2,81,

с = (45,3 – 6,9∙1) ∙2,81 = 107,90,

 

 

 

Жесткость клеефанерной балки со стенкой 18 мм не обеспечена.

Увеличим толщину стенки до 24 мм.

В = 3,14²∙10000∙10258/(750∙880²∙2,4) = 0,73.

k_ж = 1/(1 + 0,73) = 0,58;

γ = 2∙9,9∙23,0/(2,4∙90,1) = 2,11,

с = (45,3 – 6,9∙1) ∙2,11 = 81,02,

Жесткость клеефанерной балки со стенкой 24 мм обеспечена.

Проверку устойчивости фанерной стенки производим по формуле:

τ_ср= (Q_max∙S)/(I_x∙δ) ≤ φ_в.ст.R_ф.ср/γ_n,

где Q_max – расчетная поперечная сила,

R_ф.ср – сопротивление фанеры стенки срезу, определяем по табл. 10 СНиП II-25-80,

φ_в.ст = k₁∙ k₂/λ²_в.ст

коэффициент k₁ вычисляем по формуле: ,

где Е_ф90 – модуль упругости фанерной стенки в направлении поперек оси балки.

Коэффициент k₂ зависит от отношения h_в/ℓ_в:

при h_в/ℓ_в =80/880 = 1/11 k₂ = 0.45.

λ_в.ст – гибкость волнистой стенки, определяемая по формуле:

Поперечная сила в опорном сечении балки составляет:

Q_max= q_pℓ/2 = 4,63∙6,3/2 = 14,58 кН,

ℓ_в = 88 см, h _в = 8 см, δ = 24 см,

k₂ = 0,45

k₁ ∙ k₂ = 1166,73∙0,45 = 525,028,

λ² _в.ст =(100 - 2∙9,9)²/(2,4∙8) = 335,0,

φ_в.ст = 525,028/335,0 = 1,57.

τ_ср= 10^-2 (14580∙3,57)/(927955∙2,4) = 0,02 МПа ≤ φ_в.ст.R_ф.ср/γ_n = 1,57∙6/0,95 = 9,92 МПа,

Условие устойчивости выполняется.

 

Прочность на сдвиг (скалывание) клеевого соединения стенки с поясом проверяем исходя из предположения, что расчетная ширина клеевого шва равна двум глубинам заделки в паз:

h_ш =2,5δ = 2.5∙24 = 60 мм.

τ_ср= (Q∙S)/(0,6∙I_x∙2∙h_ш) ≤ R_ск./γ_n,

где 0,6 – коэффициент, учитывающий возможность некачественного склеивания пояса со стенкой.

τ_ср= 10^-2 (14580*3,57)/(0,6∙927955∙2∙6,0) = 0,007 МПа ≤ R_ск./γ_n = 1,6/0,95 = 1,68 МПа,

условие прочности выполняется.

Из условия смятия древесины нижнего пояса поперек волокон в опорной части балки находим ширину обвязочного бруса:

b = R_Б/(b_п · R_см90) = 1458/(23·24) = 2,64 см.

Принимаем брус сечением 230х230 мм.

Проверим высоту бруса, служащего распоркой вертикальных связей между стойками:

λ = В/(0,289h^тр_об) => h^тр_об = В/(0,289 λ),

где В – шаг поперечных рам здания,

λ = 1/200,

h^тр_об = 440/(0,289·200) = 7,61 см < h_об = 23 см.

Расчет производим по формуле:

σ_n = M_max/(φ_mW_бр) ≤ R_u/γ_n,

где М_max – максимальный изгибающий момент,

М_max = 4,63·6,3²/8 = 22,97 кНм.

W_бр – максимальный момент сопротивления брутто

φ_m = 140(b²/(l_расчh))k_ф,

где k_ф – коэффициент, зависящий от формы эпюры изгибающих моментов, определяемый по табл. 2 прил. 4 [7]. K_ф = 1,13.

R_u – расчетное сопротивление изгибу.

L_расч – расстояние между опорными сечениями элемента.

φ_m = 140(0,23²/(1,41·1,0))1,13 = 5,94,

σ_n = 22,97·10 ^-3/[5,94·0,1856] = 0,04 МПа < 15/0,95 = 15,79 МПа

Условие устойчивости плоской формы деформирования выполняется.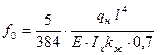
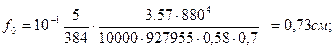