СМО с отказами
В СМО с отказами заявка, потупившая в момент, когда каналы заняты, получает «отказ», покидает СМО и в дальнейшем процессе не участвует. Если свободен хотя бы один канал, то заявка принимается к обслуживанию любым свободным каналом и обслуживается до конца.
Основные расчетные формулы 1. Вероятность того, что все каналы свободны (k=0)
где λ – интенсивность входящих требований; μ – интенсивность обслуживаемых требований;
n – число каналов обслуживания; k – число занятых каналов; τ- частота поступления заявок в единицу времени. 2. Вероятность того, что вес каналы полностью загружены (k=n), т.е. вероятность отказа в обслуживании:
а вероятность обслуживания (относительная пропускная способность системы) равна:
абсолютная пропускная способность будет:
3. Среднее число занятых обслуживанием каналов:
3. Коэффициент занятости каналов:
4. Среднее время простоя канала:
5. Среднее время простоя канала:
6. Вероятность занятости одного из каналов:
Пример. На АЗС работают 3 ТРК. Если клиент прибывает на АЗС, когда все ТРК заняты обслуживанием ранее прибывших клиентов, то он уезжает, не ожидая обслуживания. Среде число клиентов, заезжающих на АЗС в течение часа, ровно 24; среднее время обслуживания, которое тратит клиент на обслуживание ровно 5 минутам. С помощью моделей СМО с отказом определить следующие показатели: 1) вероятность того, что посетитель не будет обслужен; 2) среднюю занятость топливораздаточной колонки. Решение. По условию задачи интенсивность входящих потоков λ=24 автомобиля в час, а интенсивность обслуживаемых требований По формуле (1.1) находим вероятность отказа:
Значение 0,21 показывает, что из 100 посетителей в среднем 79 будут обслужены, а 21 – нет. Определим среднюю занятость топливораздаточной колонки по формуле (1.5.):
Это означает, что каждая топливораздаточная колонка будет занята:
рабочего дня.
|

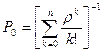 , (1.1)
, (1.1)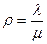 ;
; 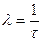 ;
; 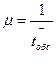 ,
,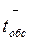 - среднее время обслуживания заявок;
- среднее время обслуживания заявок;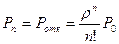 , (1.2.)
, (1.2.)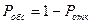 , (1.3.)
, (1.3.) . (1.4.)
. (1.4.) . (1.5.)
. (1.5.)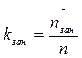 (1.6.)
(1.6.) . (1.7.)
. (1.7.) (1.8.)
(1.8.)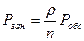 . (1.9.)
. (1.9.)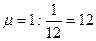 , так как 5 минут равны 1/12 часа, а
, так как 5 минут равны 1/12 часа, а 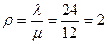 .
.
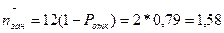 .
.



