Невооруженным глазом заметно, что данное изображение имеет блочную структуру, т.е. содержит артефакты блочности. Поскольку артефакты блочности, возникающие в горизонтальных и вертикальных направлениях, ничем не отличаются друг от друга, предложенный алгоритм будет описан только для измерения горизонтальных артефактов блочности.
Каждый блок можно представить как сумму постоянной составляющей и независимого равномерно распределенного белого шума с нулевым математическим ожиданием и неизвестной дисперсией.
Рассмотрим два соседних блока 8 × 8 пикселей  и
и  со средними значениями
со средними значениями  и
и  соответственно, где
соответственно, где  . Таким образом, эти блоки можно описать следующими формулами [5]:
. Таким образом, эти блоки можно описать следующими формулами [5]:
 ,
, 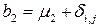 , (6)
, (6)
где  и
и  - слагаемые, являющиеся независимым равномерно распределенным белым шумом с нулевым математическим ожиданием. Когда коэффициенты ДКП соответствующих блоков
- слагаемые, являющиеся независимым равномерно распределенным белым шумом с нулевым математическим ожиданием. Когда коэффициенты ДКП соответствующих блоков  и
и  квантуются с большим шагом квантования, большинство квантованных коэффициентов равны нулю, что снижает переменные составляющие
квантуются с большим шагом квантования, большинство квантованных коэффициентов равны нулю, что снижает переменные составляющие  и
и  . В результате ступенчатая двумерная функция между
. В результате ступенчатая двумерная функция между  и
и  может стать видимой (из-за того, что
может стать видимой (из-за того, что  ), создавая артефакт блочности, как показано на рис. 1. Основываясь на этом наблюдении, мы формируем новый смещенный блок
), создавая артефакт блочности, как показано на рис. 1. Основываясь на этом наблюдении, мы формируем новый смещенный блок 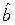 , составленный из правой половины
, составленный из правой половины  и левой половины
и левой половины  , как показано на рис. 2.
, как показано на рис. 2.

|
Рис. 2. Иллюстрация формирования нового смещенного блока 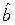
|
Артефакт блочности между блоками  и
и  может быть смоделирован как ступенчатая двумерная функция в блоке
может быть смоделирован как ступенчатая двумерная функция в блоке 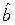 . Определим ступенчатый двумерный блок
. Определим ступенчатый двумерный блок  в новом смещенном блоке
в новом смещенном блоке 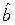 как [5]:
как [5]:
 (7)
(7)
Таким образом, смещенный блок можно представить в виде следующего выражения:
 (8)
(8)
где  – это амплитуда ступенчатой двумерной функции
– это амплитуда ступенчатой двумерной функции  ,
,  – это среднее значение блока
– это среднее значение блока 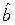 , показывающее локальную яркость фона, а
, показывающее локальную яркость фона, а  – это остаточный блок, который описывает локальную детализацию на границе исходных блоков
– это остаточный блок, который описывает локальную детализацию на границе исходных блоков  и
и  . Чем больше значение величины
. Чем больше значение величины  , тем больше артефакты блочности при неизменных яркости фона и локальной детализации. Далее применяется эффективный алгоритм на базе пространства ДКП, с помощью которого находятся коэффициенты ДКП блока
, тем больше артефакты блочности при неизменных яркости фона и локальной детализации. Далее применяется эффективный алгоритм на базе пространства ДКП, с помощью которого находятся коэффициенты ДКП блока 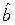 и величины параметров
и величины параметров  ,
,  и
и  .
.

 и
и  со средними значениями
со средними значениями  и
и  соответственно, где
соответственно, где  . Таким образом, эти блоки можно описать следующими формулами [5]:
. Таким образом, эти блоки можно описать следующими формулами [5]: ,
, 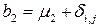 , (6)
, (6) и
и  - слагаемые, являющиеся независимым равномерно распределенным белым шумом с нулевым математическим ожиданием. Когда коэффициенты ДКП соответствующих блоков
- слагаемые, являющиеся независимым равномерно распределенным белым шумом с нулевым математическим ожиданием. Когда коэффициенты ДКП соответствующих блоков 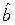 , составленный из правой половины
, составленный из правой половины 
 в новом смещенном блоке
в новом смещенном блоке  (7)
(7) (8)
(8) – это амплитуда ступенчатой двумерной функции
– это амплитуда ступенчатой двумерной функции  – это среднее значение блока
– это среднее значение блока  – это остаточный блок, который описывает локальную детализацию на границе исходных блоков
– это остаточный блок, который описывает локальную детализацию на границе исходных блоков  и
и 


