1.5.1. Алгоритм уменьшения артефактов блочности
Рассмотрим границу между двумя соседними блоками. С помощью индекса НИБ, описанного выше, вычислим значение блочности на границе двух соседних блоков. Если значение блочности  для этой границы меньше определенного порога
для этой границы меньше определенного порога  , то преобразование этой границы не требуется. Если же порог превышен:
, то преобразование этой границы не требуется. Если же порог превышен:  , то уменьшение артефактов блочности необходимо. Порог
, то уменьшение артефактов блочности необходимо. Порог  определяется эмпирически. Для того чтобы предотвратить размытие краев объектов на исходном изображении, формируется инвариантное изображение, состоящее из блоков, в которых все ДКП-коэффициенты приравниваются нулю, кроме первого коэффициента. Это изображение используется для нахождения краев объектов на исходном изображении. Блоки, которые соприкасаются с найденными краями объектов, будем называть краевыми блоками. Далее, исходя из измеренной ранее локальной видимости артефактов блочности на каждой границе каждого блока и информации о краях объектов, все границы блоков исходного изображения делятся на три следующих типа [5]:
определяется эмпирически. Для того чтобы предотвратить размытие краев объектов на исходном изображении, формируется инвариантное изображение, состоящее из блоков, в которых все ДКП-коэффициенты приравниваются нулю, кроме первого коэффициента. Это изображение используется для нахождения краев объектов на исходном изображении. Блоки, которые соприкасаются с найденными краями объектов, будем называть краевыми блоками. Далее, исходя из измеренной ранее локальной видимости артефактов блочности на каждой границе каждого блока и информации о краях объектов, все границы блоков исходного изображения делятся на три следующих типа [5]:
- Тип 1:  , дальнейшее преобразование не требуется.
, дальнейшее преобразование не требуется.
- Тип 2:  , и ни один из двух блоков, составляющих данную границу, не является краевым.
, и ни один из двух блоков, составляющих данную границу, не является краевым.
- Тип 3: 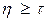 , и хотя бы один из двух блоков, составляющих данную границу, является краевым блоком.
, и хотя бы один из двух блоков, составляющих данную границу, является краевым блоком.
Для того чтобы уменьшить артефакты блочности и при этом минимально исказить исходное изображение, для трех типов границ блоков применяются разные методы обработки. Общая схема алгоритма приведена на рис. 4.

|
| Рис. 4. Общая схема алгоритма удаления блочности.
|
Ниже приведено подробное описание предложенного алгоритма уменьшения артефактов блочности.
1.5.2. Нахождение краев объектов на изображении
Поскольку все ДКП-коэффициенты изображения при декодировании доступны, инвариантное изображение может быть легко сформировано из первых коэффициентов каждого блока. При этом размер инвариантного изображения составляет 1/64 от размера исходного изображения. Далее для каждого пикселя этого изображения находится величина градиента  по следующей формуле [3]:
по следующей формуле [3]:
 (26)
(26)
Пиксель считается краевым, если  , где
, где  – это некоторый порог. Информация о краевых пикселях записывается в двоичной форме в виде матрицы. Бинарная морфологическая фильтрация [28] применяется для удаления изолированных краевых пикселей, которые могут привести к ошибкам при нахождении краев. Поскольку каждый пиксель в инвариантном изображении соответствует блоку 8 × 8 в исходном изображении, каждый блок, соответствующий краевому пикселю в инвариантном изображении, объявляется краевым блоком в исходном изображении. На рис. 5 показан пример работы алгоритма нахождения краев объектов на изображениях «Лена», «Бабуин» и «Перцы», закодированных алгоритмом JPEG с одинаковыми коэффициентами сжатия
– это некоторый порог. Информация о краевых пикселях записывается в двоичной форме в виде матрицы. Бинарная морфологическая фильтрация [28] применяется для удаления изолированных краевых пикселей, которые могут привести к ошибкам при нахождении краев. Поскольку каждый пиксель в инвариантном изображении соответствует блоку 8 × 8 в исходном изображении, каждый блок, соответствующий краевому пикселю в инвариантном изображении, объявляется краевым блоком в исходном изображении. На рис. 5 показан пример работы алгоритма нахождения краев объектов на изображениях «Лена», «Бабуин» и «Перцы», закодированных алгоритмом JPEG с одинаковыми коэффициентами сжатия  , при различных порогах
, при различных порогах  . Краевые блоки выделены черным цветом.
. Краевые блоки выделены черным цветом.
Из рис. 5 видно, что основные границы были успешно обнаружены. При этом вычислительная сложность подобного алгоритма сравнительно невысока, поскольку он работает с инвариантным изображением, и формула для вычисления  является тривиальной.
является тривиальной.
1.5.3. Алгоритм постобработки для границ второго типа
Если граница  между блоками
между блоками  и
и  принадлежит к типу 2, то это означает, что ни один из двух блоков, составляющих данную границу, не является краевым. В этом случае можно заменить в смещенном блоке
принадлежит к типу 2, то это означает, что ни один из двух блоков, составляющих данную границу, не является краевым. В этом случае можно заменить в смещенном блоке  ступенчатую двумерную функцию
ступенчатую двумерную функцию  , используемую для построения модели смещенного блока, на линейную двумерную функцию. На рис. 6 показан одномерный случай замены ступенчатой функции
, используемую для построения модели смещенного блока, на линейную двумерную функцию. На рис. 6 показан одномерный случай замены ступенчатой функции  на линейную функцию
на линейную функцию  .
.

|
| Рис. 6. Иллюстрация замены ступенчатой функции на линейную функцию
|
Используя параметры рис. 6, находим, что
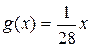 .
.
Таким образом, можно получить восемь значений пикселей линейной функции [5]:
 (27)
(27)
Линейная двумерная функция  может быть составлена из восьми строк, каждая из которых – это вектор
может быть составлена из восьми строк, каждая из которых – это вектор 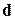 .
.
 (28)
(28)
Отметим, что матрица  является асимметричной в горизонтальном направлении и постоянной в вертикальном направлении. Поэтому ДКП линейной двумерной функции
является асимметричной в горизонтальном направлении и постоянной в вертикальном направлении. Поэтому ДКП линейной двумерной функции  , как и ДКП ступенчатой двумерной функции
, как и ДКП ступенчатой двумерной функции  , имеет лишь четыре ненулевых элемента в первой строке. Пусть вектор
, имеет лишь четыре ненулевых элемента в первой строке. Пусть вектор  – это первая строка матрицы коэффициентов ДКП линейной двумерной функции
– это первая строка матрицы коэффициентов ДКП линейной двумерной функции  . Тогда из свойства асимметрии
. Тогда из свойства асимметрии  в горизонтальном направлении следует, что
в горизонтальном направлении следует, что 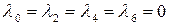 .
.
Пусть вектор  , где
, где  – первая строка матрицы коэффициентов ДКП ступенчатой двумерной функции
– первая строка матрицы коэффициентов ДКП ступенчатой двумерной функции  . Пусть блок
. Пусть блок 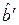 – обновленный блок после замены в блоке
– обновленный блок после замены в блоке  ступенчатой двумерной функции
ступенчатой двумерной функции  на линейную двумерную функцию
на линейную двумерную функцию  , тогда:
, тогда:
 (29)
(29)
где  определяется из выражения (15). ДКП как
определяется из выражения (15). ДКП как  , так и
, так и  имеют только четыре ненулевых элемента в своих первых строках, которые представлены векторами
имеют только четыре ненулевых элемента в своих первых строках, которые представлены векторами  и
и  соответственно. Применение формулы (29) в пространстве ДКП выглядит следующим образом:
соответственно. Применение формулы (29) в пространстве ДКП выглядит следующим образом:

 (30)
(30)
где  – это матрица коэффициентов ДКП для блока
– это матрица коэффициентов ДКП для блока 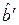 .
.
Блок  затем используется для преобразования обоих блоков
затем используется для преобразования обоих блоков  и
и  (рис. 2.2) посредством перемножения матриц, похожего на преобразование (11). Но в связи с тем, что только элементы первой строки матрицы
(рис. 2.2) посредством перемножения матриц, похожего на преобразование (11). Но в связи с тем, что только элементы первой строки матрицы  изменяются для получения матрицы
изменяются для получения матрицы  , в матрицах
, в матрицах  и
и  подвергнутся изменению также только элементы первой строки, что видно из формулы (11). Поэтому можно использовать следующий простой алгоритм преобразования блоков
подвергнутся изменению также только элементы первой строки, что видно из формулы (11). Поэтому можно использовать следующий простой алгоритм преобразования блоков  и
и  . Пусть
. Пусть  и
и  – это дельта вектора для матриц
– это дельта вектора для матриц  и
и  соответственно. Тогда
соответственно. Тогда

где  и
и  – матрицы из (11). Окончательно блоки
– матрицы из (11). Окончательно блоки  и
и  преобразуются по следующему алгоритму:
преобразуются по следующему алгоритму:
 (31)
(31)
Отметим, что  и
и  – это постоянные вектора, которые могут быть вычислены заранее и сохранены.
– это постоянные вектора, которые могут быть вычислены заранее и сохранены.
1.5.4. Алгоритм постфильтрации в пространстве ДКП
границ второго и третьего типа
После применения к блокам  и
и 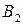 преобразования (31) новые артефакты, хотя и менее заметные, могут возникать на границе между блоками
преобразования (31) новые артефакты, хотя и менее заметные, могут возникать на границе между блоками  и
и  . Чтобы подавить вновь созданные искажения, к обоим измененным блокам
. Чтобы подавить вновь созданные искажения, к обоим измененным блокам  и
и 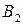 применяется метод постфильтрации в пространстве ДКП. Этот же метод применяется и для границ третьего типа с целью уменьшения артефактов блочности [5].
применяется метод постфильтрации в пространстве ДКП. Этот же метод применяется и для границ третьего типа с целью уменьшения артефактов блочности [5].
Пусть  – это блок 8 × 8 m -той строки и n -того столбца изображения, а блок
– это блок 8 × 8 m -той строки и n -того столбца изображения, а блок 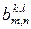 – это блок, сдвинутый относительно блока
– это блок, сдвинутый относительно блока  на
на  пикселей по оси
пикселей по оси  и на
и на  пикселей по оси
пикселей по оси  , как показано на рис. 4.4.
, как показано на рис. 4.4.

|
Рис. 7. Иллюстрация смещенного блока при  и и 
|
Из рис. 7 видно, что при  и
и  блоки
блоки  и
и 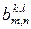 будут частично перекрываться. Пусть
будут частично перекрываться. Пусть  и
и  – матрицы коэффициентов ДКП блоков
– матрицы коэффициентов ДКП блоков  и
и 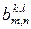 соответственно. Тогда постфильтрация в пространстве ДКП для преобразования
соответственно. Тогда постфильтрация в пространстве ДКП для преобразования  выглядит следующим образом:
выглядит следующим образом:
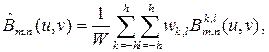 (32)
(32)
где  – это отфильтрованный блок в пространстве ДКП,
– это отфильтрованный блок в пространстве ДКП,  – максимальное смещение по осям
– максимальное смещение по осям  и
и  ,
,  – весовые коэффициенты блоков
– весовые коэффициенты блоков  , а
, а  – это сумма всех весовых коэффициентов, определяемая по формуле:
– это сумма всех весовых коэффициентов, определяемая по формуле:
 (33)
(33)
Блоки в пространстве ДКП  могут быть найдены непосредственно из четырех соседних блоков, с которыми они перекрываются [29] по формуле:
могут быть найдены непосредственно из четырех соседних блоков, с которыми они перекрываются [29] по формуле:
 (34)
(34)
где  и
и  – это матрицы коэффициентов ДКП от матриц
– это матрицы коэффициентов ДКП от матриц  и
и  соответственно. Матрицы
соответственно. Матрицы  и
и  определены в [30]. Непосредственное применение формулы (34) приводит к большому увеличению вычислительной сложности алгоритма постобработки. Разработано несколько быстрых алгоритмов [31, 32-33], которые уменьшают вычислительную сложность (34).
определены в [30]. Непосредственное применение формулы (34) приводит к большому увеличению вычислительной сложности алгоритма постобработки. Разработано несколько быстрых алгоритмов [31, 32-33], которые уменьшают вычислительную сложность (34).
1.5.5. Ограничение коэффициентов ДКП после процедуры постфильтрации
После процедуры постфильтрации, описанной выше, к каждому коэффициенту ДКП обрабатываемых блоков применяется операция ограничения [34, 35], с тем, чтобы все коэффициенты оставались в рамках своих исходных интервалов. Поскольку параметры квантования известны на приемной стороне, соответствующие интервалы квантования [  ] для исходного коэффициента
] для исходного коэффициента 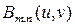 находятся по формулам:
находятся по формулам:
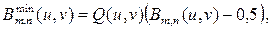 (35)
(35)
 (36)
(36)
где  – это шаг квантования для коэффициента
– это шаг квантования для коэффициента 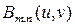 . Преобразованный коэффициент
. Преобразованный коэффициент  заключается в рамках [
заключается в рамках [  ] с помощью следующего алгоритма:
] с помощью следующего алгоритма:

(37)
1.5.6. Алгоритм модифицированной
билатеральной фильтрации
Модифицированный билатеральный фильтр отличается от классического билатерального фильтра способностью различать границы блоков с границами объектов самого изображения. Это позволяет осуществлять более мягкую фильтрацию без размытия границ объектов.
Рассмотрим подробнее алгоритм модифицированной билатеральной фильтрации, схема которого представлена на рис. 8. В структурную схему модифицированного билатерального фильтра включены дополнительные модули, такие как выделение краевых блоков и построение карты блочности.

|
| Рис. 8. Схема алгоритма модифицированного билатерального фильтра
|
Модуль выделения краевых блоков позволяет разделить границы блоков и границы (края) объектов в исходном сжатом изображении (рис. 9). Выделение краевых блоков происходит на основе инвариантного изображения  . Оно формируется из первых коэффициентов ДКП всех блоков исходного изображения, и каждый его элемент, таким образом, отвечает за целый блок исходного изображения.
. Оно формируется из первых коэффициентов ДКП всех блоков исходного изображения, и каждый его элемент, таким образом, отвечает за целый блок исходного изображения.
 В полученном инвариантном изображении находятся краевые пиксели, т. е. пиксели, соприкасающиеся с границами объектов изображения. Для того, чтобы определить, является ли данный пиксель краевым, величина градиента
В полученном инвариантном изображении находятся краевые пиксели, т. е. пиксели, соприкасающиеся с границами объектов изображения. Для того, чтобы определить, является ли данный пиксель краевым, величина градиента  для него сравнивается с порогом T, определяемым из опыта:
для него сравнивается с порогом T, определяемым из опыта:
 где
где
(38)
Такое выделение границ на изображении осуществляется с применением масок 3×3, отвечающих оператору Собела (рис. 10) [3]:


Рис. 10. Маски оператора Собела
Блок исходного изображения считается краевым, если соответствующий ему пиксель инвариантного изображения - краевой. На рис. 11 представлен результат выделения краевых пикселей для сжатого изображения «Барбара» (CR = 0,2 bpp)
Вычисляется коэффициент блочности η на границе смежных блоков:
(39)
Значения коэффициента блочности, вычисленные для каждой из границ блоков, сохраняются в виде матрицы чисел  , где
, где  . Назовем эту матрицу картой блочности. На рис. 12 (а) приведен фрагмент карты блочности. Однако на основе карты блочности, полученной таким образом, не возможно эффективно устранить эффект блочности. Искажение, сосредоточенное на границе смежных блоков, при последующей билатеральной фильтрации будет сдвигаться внутрь блока.
. Назовем эту матрицу картой блочности. На рис. 12 (а) приведен фрагмент карты блочности. Однако на основе карты блочности, полученной таким образом, не возможно эффективно устранить эффект блочности. Искажение, сосредоточенное на границе смежных блоков, при последующей билатеральной фильтрации будет сдвигаться внутрь блока.
Для устранения данного отрицательного эффекта вводится матрица масштабирующих коэффициентов  , где
, где  . Она позволяет получить значения блочности вдали от границы блоков. Матрица масштабирующих коэффициентов показана на рис. 12 (б).
. Она позволяет получить значения блочности вдали от границы блоков. Матрица масштабирующих коэффициентов показана на рис. 12 (б).
Искомая карта блочности 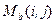 будет получена поэлементным перемножением локальной области исходной карты блочности на матрицу масштабирующих коэффициентов последовательно по всей карте блочности.
будет получена поэлементным перемножением локальной области исходной карты блочности на матрицу масштабирующих коэффициентов последовательно по всей карте блочности.
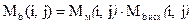 (40)
(40)
Фрагмент искомой карты блочности приведен на рис. 12 (в).
|
(а) (б) (в)
|
| Рис. 12. Пример преобразования карты блочности: (а) исходная карта блочности, (б) матрица масштабирующих коэффициентов, (в) искомая карта блочности.
|
На рис. 13 приведен пример карты блочности (б), полученный для сжатого изображения Барбара (а). Чем темнее участки карты, тем параметры фильтрации будут грубее. Светлые же участки соответствуют областям изображения с высокой детализацией и границами объектов. К ним необходимо применять фильтрацию с мягкими параметрами, чтобы избежать размытия и искажений.
В исходном изображении выделяется локальная область, над которой будет производиться фильтрация. В зависимости от характеристик пикселей, принадлежащих этой области, и ранее построенной карты блочности происходит вычисление оптимальных параметров билатерального фильтра и осуществляется фильтрация выбранной области.

Затем в исходном изображении выделяется следующий блок, вычисляются параметры фильтра, осуществляется фильтрация и т. д. Процесс заканчивается после того, как будет обработана последняя область, на выходе получаем обработанное изображение с уменьшенными артефактами блочности.

 для этой границы меньше определенного порога
для этой границы меньше определенного порога  , то преобразование этой границы не требуется. Если же порог превышен:
, то преобразование этой границы не требуется. Если же порог превышен:  , то уменьшение артефактов блочности необходимо. Порог
, то уменьшение артефактов блочности необходимо. Порог  определяется эмпирически. Для того чтобы предотвратить размытие краев объектов на исходном изображении, формируется инвариантное изображение, состоящее из блоков, в которых все ДКП-коэффициенты приравниваются нулю, кроме первого коэффициента. Это изображение используется для нахождения краев объектов на исходном изображении. Блоки, которые соприкасаются с найденными краями объектов, будем называть краевыми блоками. Далее, исходя из измеренной ранее локальной видимости артефактов блочности на каждой границе каждого блока и информации о краях объектов, все границы блоков исходного изображения делятся на три следующих типа [5]:
определяется эмпирически. Для того чтобы предотвратить размытие краев объектов на исходном изображении, формируется инвариантное изображение, состоящее из блоков, в которых все ДКП-коэффициенты приравниваются нулю, кроме первого коэффициента. Это изображение используется для нахождения краев объектов на исходном изображении. Блоки, которые соприкасаются с найденными краями объектов, будем называть краевыми блоками. Далее, исходя из измеренной ранее локальной видимости артефактов блочности на каждой границе каждого блока и информации о краях объектов, все границы блоков исходного изображения делятся на три следующих типа [5]: , дальнейшее преобразование не требуется.
, дальнейшее преобразование не требуется.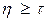 , и хотя бы один из двух блоков, составляющих данную границу, является краевым блоком.
, и хотя бы один из двух блоков, составляющих данную границу, является краевым блоком.
 по следующей формуле [3]:
по следующей формуле [3]: (26)
(26) , где
, где  – это некоторый порог. Информация о краевых пикселях записывается в двоичной форме в виде матрицы. Бинарная морфологическая фильтрация [28] применяется для удаления изолированных краевых пикселей, которые могут привести к ошибкам при нахождении краев. Поскольку каждый пиксель в инвариантном изображении соответствует блоку 8 × 8 в исходном изображении, каждый блок, соответствующий краевому пикселю в инвариантном изображении, объявляется краевым блоком в исходном изображении. На рис. 5 показан пример работы алгоритма нахождения краев объектов на изображениях «Лена», «Бабуин» и «Перцы», закодированных алгоритмом JPEG с одинаковыми коэффициентами сжатия
– это некоторый порог. Информация о краевых пикселях записывается в двоичной форме в виде матрицы. Бинарная морфологическая фильтрация [28] применяется для удаления изолированных краевых пикселей, которые могут привести к ошибкам при нахождении краев. Поскольку каждый пиксель в инвариантном изображении соответствует блоку 8 × 8 в исходном изображении, каждый блок, соответствующий краевому пикселю в инвариантном изображении, объявляется краевым блоком в исходном изображении. На рис. 5 показан пример работы алгоритма нахождения краев объектов на изображениях «Лена», «Бабуин» и «Перцы», закодированных алгоритмом JPEG с одинаковыми коэффициентами сжатия  , при различных порогах
, при различных порогах  и
и  принадлежит к типу 2, то это означает, что ни один из двух блоков, составляющих данную границу, не является краевым. В этом случае можно заменить в смещенном блоке
принадлежит к типу 2, то это означает, что ни один из двух блоков, составляющих данную границу, не является краевым. В этом случае можно заменить в смещенном блоке  ступенчатую двумерную функцию
ступенчатую двумерную функцию  , используемую для построения модели смещенного блока, на линейную двумерную функцию. На рис. 6 показан одномерный случай замены ступенчатой функции
, используемую для построения модели смещенного блока, на линейную двумерную функцию. На рис. 6 показан одномерный случай замены ступенчатой функции  на линейную функцию
на линейную функцию  .
.
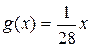 .
. (27)
(27) может быть составлена из восьми строк, каждая из которых – это вектор
может быть составлена из восьми строк, каждая из которых – это вектор 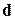 .
. (28)
(28) – это первая строка матрицы коэффициентов ДКП линейной двумерной функции
– это первая строка матрицы коэффициентов ДКП линейной двумерной функции 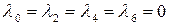 .
. , где
, где  – первая строка матрицы коэффициентов ДКП ступенчатой двумерной функции
– первая строка матрицы коэффициентов ДКП ступенчатой двумерной функции  . Пусть блок
. Пусть блок 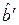 – обновленный блок после замены в блоке
– обновленный блок после замены в блоке  ступенчатой двумерной функции
ступенчатой двумерной функции  (29)
(29) определяется из выражения (15). ДКП как
определяется из выражения (15). ДКП как  соответственно. Применение формулы (29) в пространстве ДКП выглядит следующим образом:
соответственно. Применение формулы (29) в пространстве ДКП выглядит следующим образом:
 (30)
(30) – это матрица коэффициентов ДКП для блока
– это матрица коэффициентов ДКП для блока  и
и  (рис. 2.2) посредством перемножения матриц, похожего на преобразование (11). Но в связи с тем, что только элементы первой строки матрицы
(рис. 2.2) посредством перемножения матриц, похожего на преобразование (11). Но в связи с тем, что только элементы первой строки матрицы  изменяются для получения матрицы
изменяются для получения матрицы  и
и  – это дельта вектора для матриц
– это дельта вектора для матриц 
 и
и  – матрицы из (11). Окончательно блоки
– матрицы из (11). Окончательно блоки  (31)
(31) и
и 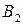 преобразования (31) новые артефакты, хотя и менее заметные, могут возникать на границе между блоками
преобразования (31) новые артефакты, хотя и менее заметные, могут возникать на границе между блоками  . Чтобы подавить вновь созданные искажения, к обоим измененным блокам
. Чтобы подавить вновь созданные искажения, к обоим измененным блокам  – это блок 8 × 8 m -той строки и n -того столбца изображения, а блок
– это блок 8 × 8 m -той строки и n -того столбца изображения, а блок 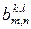 – это блок, сдвинутый относительно блока
– это блок, сдвинутый относительно блока  пикселей по оси
пикселей по оси  и на
и на  , как показано на рис. 4.4.
, как показано на рис. 4.4.
 и
и 
 и
и  блоки
блоки  и
и  – матрицы коэффициентов ДКП блоков
– матрицы коэффициентов ДКП блоков 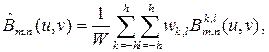 (32)
(32) – это отфильтрованный блок в пространстве ДКП,
– это отфильтрованный блок в пространстве ДКП,  – максимальное смещение по осям
– максимальное смещение по осям  – весовые коэффициенты блоков
– весовые коэффициенты блоков  , а
, а  – это сумма всех весовых коэффициентов, определяемая по формуле:
– это сумма всех весовых коэффициентов, определяемая по формуле: (33)
(33) (34)
(34) и
и  – это матрицы коэффициентов ДКП от матриц
– это матрицы коэффициентов ДКП от матриц  и
и  соответственно. Матрицы
соответственно. Матрицы  ] для исходного коэффициента
] для исходного коэффициента 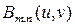 находятся по формулам:
находятся по формулам: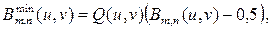 (35)
(35) (36)
(36) – это шаг квантования для коэффициента
– это шаг квантования для коэффициента  заключается в рамках [
заключается в рамках [ 

 . Оно формируется из первых коэффициентов ДКП всех блоков исходного изображения, и каждый его элемент, таким образом, отвечает за целый блок исходного изображения.
. Оно формируется из первых коэффициентов ДКП всех блоков исходного изображения, и каждый его элемент, таким образом, отвечает за целый блок исходного изображения. В полученном инвариантном изображении находятся краевые пиксели, т. е. пиксели, соприкасающиеся с границами объектов изображения. Для того, чтобы определить, является ли данный пиксель краевым, величина градиента
В полученном инвариантном изображении находятся краевые пиксели, т. е. пиксели, соприкасающиеся с границами объектов изображения. Для того, чтобы определить, является ли данный пиксель краевым, величина градиента  для него сравнивается с порогом T, определяемым из опыта:
для него сравнивается с порогом T, определяемым из опыта: где
где






 , где
, где  . Назовем эту матрицу картой блочности. На рис. 12 (а) приведен фрагмент карты блочности. Однако на основе карты блочности, полученной таким образом, не возможно эффективно устранить эффект блочности. Искажение, сосредоточенное на границе смежных блоков, при последующей билатеральной фильтрации будет сдвигаться внутрь блока.
. Назовем эту матрицу картой блочности. На рис. 12 (а) приведен фрагмент карты блочности. Однако на основе карты блочности, полученной таким образом, не возможно эффективно устранить эффект блочности. Искажение, сосредоточенное на границе смежных блоков, при последующей билатеральной фильтрации будет сдвигаться внутрь блока. . Она позволяет получить значения блочности вдали от границы блоков. Матрица масштабирующих коэффициентов показана на рис. 12 (б).
. Она позволяет получить значения блочности вдали от границы блоков. Матрица масштабирующих коэффициентов показана на рис. 12 (б).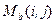 будет получена поэлементным перемножением локальной области исходной карты блочности на матрицу масштабирующих коэффициентов последовательно по всей карте блочности.
будет получена поэлементным перемножением локальной области исходной карты блочности на матрицу масштабирующих коэффициентов последовательно по всей карте блочности.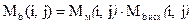 (40)
(40)




