Представление модели блочности в пространстве ДКП
Для перехода в область ДКП-коэффициентов определим две матрицы
где
Используя свойства линейности и дистрибутивности ДКП, легко получить отображение (9) в пространстве ДКП.
где
где
Таким образом, параметры из (8) могут быть посчитаны по формулам:
Пусть
Благодаря разреженности коэффициентов ДКП, предложенный алгоритм гораздо более эффективен, чем традиционные методы, такие как [6-11], даже если используются быстрые алгоритмы ДКП [12, 13-21]. Измерение артефактов блочности с учетом В большинстве случаев человек является конечным получателем визуальной информации. Поэтому измерение артефактов блочности с учетом известных характеристик ЗСЧ является целесообразным для оценки видимости артефактов блочности [22, 23-24]. Структурная маскировка, возникающая на изображениях с большим количеством мелких деталей, и яркостная маскировка – это две хорошо изученные характеристики ЗСЧ, которые в значительной степени влияют на восприятие артефактов блочности [24]. Рассмотрим сначала структурную маскировку. Для того чтобы использовать эту характеристику человеческой зрительной системы, предположим, что общая детализированность каждого блока – это просто сумма детализированностей по всем пространственным частотам, причем амплитуда каждой составляющей этой суммы равна соответствующему коэффициенту ДКП. Эффект маскировки также зависит от относительной ориентации сигнала маскировки [3,25,26]. Поскольку артефакты блочности возникают только в двух конкретных направлениях (вертикальном и горизонтальном), определим две по-разному ориентированные детализированности (вертикальную
Для вертикальных артефактов блочности преобладает эффект маскировки за счет горизонтальной детализированности, поэтому общая детализированность определяется по формуле
Общая детализированность для горизонтальных артефактов блочности определяется аналогично:
где Также необходимо учитывать яркостную маскировку: видимость артефактов блочности зависит от локальной яркости фона. С учетом обоих эффектов маскировки итоговое значение видимости артефактов блочности на границе двух соседних блоков
где Для вертикальных артефактов блочности может быть применен аналогичный метод. Результатом работы описанного выше алгоритма является вычисление видимости артефактов блочности на границе двух соседних блоков Локальные значения блочности могут быть объединены для получения численного значения блочности для всего изображения с целью оценки его качества.
где
|

 и
и 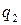 следующим образом [5]:
следующим образом [5]:
 (9)
(9)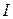 – это тождественная (единичная) матрица, а
– это тождественная (единичная) матрица, а  – нулевая матрица. Представим смещенный блок
– нулевая матрица. Представим смещенный блок 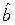 в виде
в виде (10)
(10) (11)
(11) ,
,  ,
,  ,
, 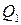 и
и  – это матрицы коэффициентов ДКП для блоков
– это матрицы коэффициентов ДКП для блоков  ,
,  ,
,  не разрежены. Это означает, что для получения
не разрежены. Это означает, что для получения  и матрица разности
и матрица разности 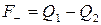 содержат много нулей (более 50% от всех элементов), поэтому значительная экономия в вычислительных операциях может быть достигнута с помощью следующего уравнения:
содержат много нулей (более 50% от всех элементов), поэтому значительная экономия в вычислительных операциях может быть достигнута с помощью следующего уравнения: (12)
(12) , а
, а  . Отметим, что ДКП ступенчатой двумерной функции
. Отметим, что ДКП ступенчатой двумерной функции  имеет лишь четыре ненулевых элемента в первой строке, поскольку
имеет лишь четыре ненулевых элемента в первой строке, поскольку  – первая строка матрицы коэффициентов ДКП ступенчатой двумерной функции
– первая строка матрицы коэффициентов ДКП ступенчатой двумерной функции  . Из свойства унитарности ДКП получаем, что
. Из свойства унитарности ДКП получаем, что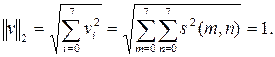 (13)
(13) (14)
(14) (15)
(15) – это матрица коэффициентов ДКП остаточного блока
– это матрица коэффициентов ДКП остаточного блока  . Тогда
. Тогда 

 (16)
(16) и горизонтальную
и горизонтальную  ) следующим образом:
) следующим образом:
 (17)
(17) (18)
(18) (19)
(19)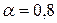 .
. определяется следующим образом [27, 5]:
определяется следующим образом [27, 5]: (20)
(20) и
и  определяются из выражений (14) и (15) соответственно,
определяются из выражений (14) и (15) соответственно, 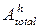 – это общая горизонтальная детализированность блока
– это общая горизонтальная детализированность блока  и
и 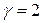 .
. (21)
(21) – это общее число границ между всеми блоками изображения,
– это общее число границ между всеми блоками изображения,  – это глобальное значение блочности всего изображения, а показатель степени
– это глобальное значение блочности всего изображения, а показатель степени 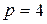 .
.


