Пример 2. Решение. Оператор A линеен
Решение. Оператор A линеен. Докажем неравенство ограниченности:
Значит, оператор А ограничен, причем В отличие от предыдущих примеров, здесь не существует ненулевого вектора, при котором неравенство (3) превращается в равенство (подумайте, почему). Поэтому будем подбирать ненулевые векторы х так, чтобы обе части (3) сколь угодно мало отличались друг от друга. Возьмём вектор
в) Оператор взвешенного сдвига.
Пример 1. Решение. Oчевидно, что оператор A линеен. Докажем его ограниченность:
поскольку, как легко проверить,
Пример 2.
Решение. Oчевидно, что оператор A линеен. Докажем его ограни-ченность. Имеем
(мы воспользовались тем, что Как и в примере 2 пункта б), не существует ненулевого вектора, при котором неравенство (5) превращается в равенство (подумайте, почему). Поэтому будем подбирать ненулевые векторы х так, чтобы обе части (5) сколь угодно мало отличались друг от друга. Возьмём последовательность
Значит,
Из полученных неравенств следует, что
г) Интегральный оператор, действующий из X в Y.
Пример 1. Решение. Из свойства линейности интеграла следует, что А – линейный оператор. Далее,
Значит, оператор А ограничен, причем
Легко видеть, что Вычислим
Следовательно, Окончательно получаем, что
3. Для данных нормированных пространств X, Y,последовательности операторов
Пример 1. Решение. 1) Заметим, что при всех
(остаток сходящегося ряда стремится к 0). Значит, последовательность 2) Возьмем вектор
Следовательно,
|

 ,
, 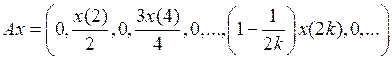 .
. . (3)
. (3) .
. (единица стоит на 2 k -м месте). Тогда имеем
(единица стоит на 2 k -м месте). Тогда имеем  , откуда
, откуда 
 (см. решение примера 1). Ввиду произвольности k отсюда следует, что
(см. решение примера 1). Ввиду произвольности k отсюда следует, что  (почему?). Окончательно получаем
(почему?). Окончательно получаем  .
. .
.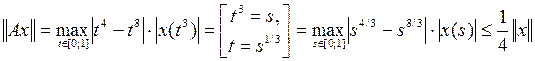 , (4)
, (4) . Следовательно,
. Следовательно,  . Так как при
. Так как при  неравенство (4) превращается в равенство, то
неравенство (4) превращается в равенство, то  (см. решения предыдущих примеров). Итак,
(см. решения предыдущих примеров). Итак, 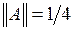 .
.
 .
.


 ). Значит,
). Значит,  .
. , состоящую из функций, сосредоточенных в окрестности точки
, состоящую из функций, сосредоточенных в окрестности точки  и таких, что
и таких, что  . Тогда
. Тогда .
.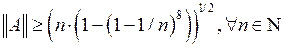 . Перейдем в последнем неравенстве к пределу при
. Перейдем в последнем неравенстве к пределу при  . Воспользовавшись тем, что
. Воспользовавшись тем, что  при
при  , получим, что
, получим, что .
. .
. .
.
 . (6)
. (6) , но эта функция не принадлежит
, но эта функция не принадлежит 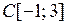 . Возьмем следующую последовательность функций из
. Возьмем следующую последовательность функций из  при больших n (сделайте чертеж):
при больших n (сделайте чертеж):
 в
в  в
в  . Так как функция
. Так как функция 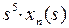 четная, то
четная, то
 .
. , а потому
, а потому  и оператора
и оператора  установить: 1) сходится ли
установить: 1) сходится ли 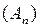 поточечно (сильно) к оператору А; 2) сходится ли
поточечно (сильно) к оператору А; 2) сходится ли  .
.
 при
при 
 из l 1. Так как
из l 1. Так как  , то
, то
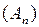 не сходится по норме к оператору А.
не сходится по норме к оператору А.


