1. При каких значениях параметра 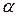 обратим данный оператор
обратим данный оператор  ? Найдите обратный оператор
? Найдите обратный оператор  , когда он существует.
, когда он существует.
Пример 1. 
 .
.
Решение. В соответствии с определением обратного оператора рассмотрим уравнение  . В нашем случае оно равносильно следующей системе линейных уравнений с параметром:
. В нашем случае оно равносильно следующей системе линейных уравнений с параметром:

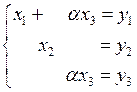 (1)
(1)
Обратный оператор  существует тогда и только тогда, когда эта система имеет единственное решение при любом у из
существует тогда и только тогда, когда эта система имеет единственное решение при любом у из 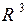 . По правилу Крамера это произойдет тогда и только тогда, когда главный определитель
. По правилу Крамера это произойдет тогда и только тогда, когда главный определитель 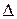 этой системы отличен от нуля. Но легко подсчитать, что
этой системы отличен от нуля. Но легко подсчитать, что
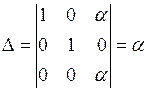 .
.
Таким образом, обратный оператор существует тогда и только тогда, когда 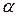
 . Решая при этих значениях параметра систему (1), получим
. Решая при этих значениях параметра систему (1), получим  Следовательно,
Следовательно,
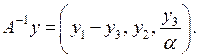
2. Пусть  Доказать, что существует непрерывный обратный оператор
Доказать, что существует непрерывный обратный оператор  , и построить его.
, и построить его.
Пример 1. 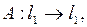

Решение. Очевидно, что А – линейный оператор. Докажем, что А является биекцией. Рассмотрим уравнение  , которое равно-сильно системе уравнений
, которое равно-сильно системе уравнений
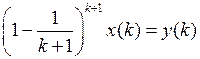 ,
, 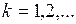 .
.
Отсюда
 . (2)
. (2)
Но последовательность  ограничена сверху, поскольку является сходящейся:
ограничена сверху, поскольку является сходящейся: 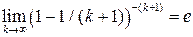 . Если С – одна из ее верхних границ, то
. Если С – одна из ее верхних границ, то
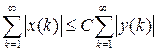
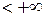 , (3)
, (3)
а потому  . Мы получили, что для любого
. Мы получили, что для любого  уравнение
уравнение  имеет единственное решение х из пространства
имеет единственное решение х из пространства  . Значит, А – биекция. Более того, из (2) следует, что обратный оператор
. Значит, А – биекция. Более того, из (2) следует, что обратный оператор  задается формулой
задается формулой
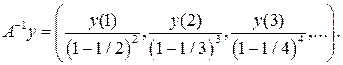
Ограниченность этого оператора следует из оценки (см. (3))
 .
.
Пример 2. 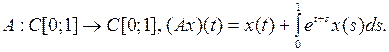
Решение. Очевидно, что А – линейный оператор. Запишем его в виде
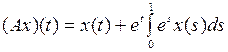 ,
,
и рассмотрим уравнение  , то есть
, то есть
 . (4)
. (4)
Пусть
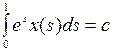 . (5)
. (5)
Тогда (4) примет вид  , откуда
, откуда 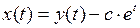 . Мы получили общий вид решения уравнения (4) с неопределенным коэффициентом с. Подставив это выражение в (5), без труда находим, что
. Мы получили общий вид решения уравнения (4) с неопределенным коэффициентом с. Подставив это выражение в (5), без труда находим, что
 .
.
Таким образом,
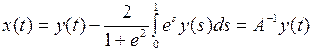 . (6)
. (6)
Итак, для любого  уравнение (4) имеет единственное решение из
уравнение (4) имеет единственное решение из 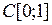 . Значит, оператор А обратим, причем обратный оператор вычисляется по формуле (6).
. Значит, оператор А обратим, причем обратный оператор вычисляется по формуле (6).
Непрерывность обратного оператора вытекает из теоремы об оценке интеграла. Действительно, по этой теореме при всех t имеем

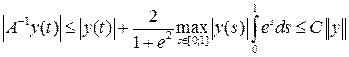 ,
,
а потому выполняется неравенство ограниченности  (другое доказательство непрерывности получается из (6) с помощью теоремы о предельном переходе под знаком интеграла Римана).
(другое доказательство непрерывности получается из (6) с помощью теоремы о предельном переходе под знаком интеграла Римана).
3. Пусть 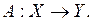
1) Что представляет собой множество значений 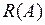 оператора А?
оператора А?
2) Существует ли на 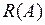 левый обратный оператор
левый обратный оператор  ?
?
3) Является ли оператор 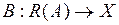 ограниченным (в случае, если он существует)?
ограниченным (в случае, если он существует)?
4) Существует ли обратный оператор  ?
?
Пример 1. 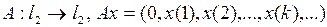 .
.
Решение. Очевидно, что
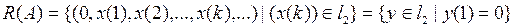 –
–
множество всех точек из пространства 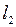 , первая координата которых равна нулю. Заметим, что
, первая координата которых равна нулю. Заметим, что 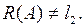
Так как уравнение 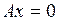 очевидно имеет только нулевое решение, то
очевидно имеет только нулевое решение, то 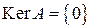 . А это, как известно, равносильно тому, что левый обратный оператор
. А это, как известно, равносильно тому, что левый обратный оператор  существует. Решая уравнение
существует. Решая уравнение  , находим, что
, находим, что
 .
.
Оператор 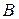 ограничен, так как
ограничен, так как 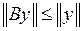 .
.
Поскольку 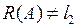 , то оператор А не является сюрьекцией. Следовательно, А необратим.
, то оператор А не является сюрьекцией. Следовательно, А необратим.
Пример 2.  .
.
Решение. По теореме о дифференцировании интеграла с перемен-ным верхним пределом (теореме Барроу) функция 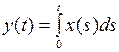 дифференцируема, причем
дифференцируема, причем 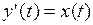 . Значит,
. Значит, 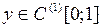 . Кроме того, очевидно, что
. Кроме того, очевидно, что 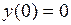 .
.
Обратно, если 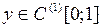 и
и 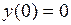 , то по формуле Ньютона-Лейбница имеем
, то по формуле Ньютона-Лейбница имеем  . Поэтому
. Поэтому
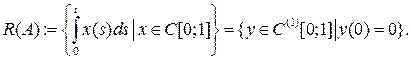
Рассмотрим оператор дифференцирования 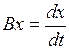 . Поскольку (снова по теореме Барроу)
. Поскольку (снова по теореме Барроу)
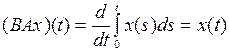
при всех 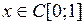 , то
, то  – левый обратный для оператора А.
– левый обратный для оператора А.
Покажем, что  не является ограниченным оператором. Допустим противное, т. е.
не является ограниченным оператором. Допустим противное, т. е.
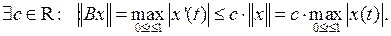
Полагая здесь 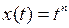
 , получаем
, получаем 
 . Противоречие.
. Противоречие.
Поскольку  , оператор А не является сюръекцией. Следовательно, не существует
, оператор А не является сюръекцией. Следовательно, не существует  .
.
4. Пусть 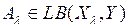 , где
, где 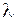 – числовой параметр,
– числовой параметр, 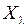 , Y − банаховы пространства. Выяснить, при каких значениях
, Y − банаховы пространства. Выяснить, при каких значениях 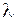 существует обратный оператор к оператору
существует обратный оператор к оператору 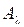 , и построить его. При каких значениях
, и построить его. При каких значениях 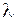 оператор
оператор 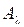 непрерывно обратим?
непрерывно обратим?

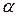 обратим данный оператор
обратим данный оператор  ? Найдите обратный оператор
? Найдите обратный оператор  , когда он существует.
, когда он существует.
 .
. . В нашем случае оно равносильно следующей системе линейных уравнений с параметром:
. В нашем случае оно равносильно следующей системе линейных уравнений с параметром: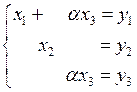 (1)
(1)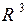 . По правилу Крамера это произойдет тогда и только тогда, когда главный определитель
. По правилу Крамера это произойдет тогда и только тогда, когда главный определитель 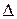 этой системы отличен от нуля. Но легко подсчитать, что
этой системы отличен от нуля. Но легко подсчитать, что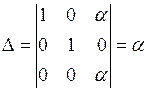 .
. . Решая при этих значениях параметра систему (1), получим
. Решая при этих значениях параметра систему (1), получим  Следовательно,
Следовательно,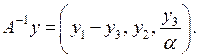
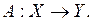 Доказать, что существует непрерывный обратный оператор
Доказать, что существует непрерывный обратный оператор 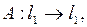

 , которое равно-сильно системе уравнений
, которое равно-сильно системе уравнений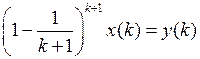 ,
, 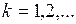 .
. . (2)
. (2) ограничена сверху, поскольку является сходящейся:
ограничена сверху, поскольку является сходящейся: 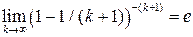 . Если С – одна из ее верхних границ, то
. Если С – одна из ее верхних границ, то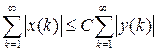
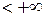 , (3)
, (3) . Мы получили, что для любого
. Мы получили, что для любого  уравнение
уравнение  . Значит, А – биекция. Более того, из (2) следует, что обратный оператор
. Значит, А – биекция. Более того, из (2) следует, что обратный оператор 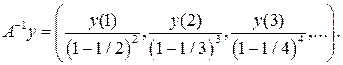
 .
.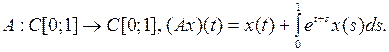
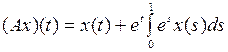 ,
, . (4)
. (4)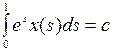 . (5)
. (5) , откуда
, откуда 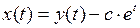 . Мы получили общий вид решения уравнения (4) с неопределенным коэффициентом с. Подставив это выражение в (5), без труда находим, что
. Мы получили общий вид решения уравнения (4) с неопределенным коэффициентом с. Подставив это выражение в (5), без труда находим, что .
.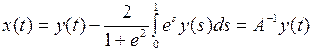 . (6)
. (6) уравнение (4) имеет единственное решение из
уравнение (4) имеет единственное решение из 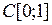 . Значит, оператор А обратим, причем обратный оператор вычисляется по формуле (6).
. Значит, оператор А обратим, причем обратный оператор вычисляется по формуле (6).
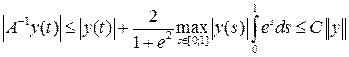 ,
, (другое доказательство непрерывности получается из (6) с помощью теоремы о предельном переходе под знаком интеграла Римана).
(другое доказательство непрерывности получается из (6) с помощью теоремы о предельном переходе под знаком интеграла Римана).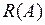 оператора А?
оператора А? ?
?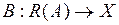 ограниченным (в случае, если он существует)?
ограниченным (в случае, если он существует)?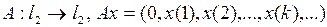 .
.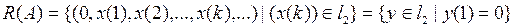 –
–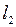 , первая координата которых равна нулю. Заметим, что
, первая координата которых равна нулю. Заметим, что 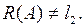
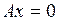 очевидно имеет только нулевое решение, то
очевидно имеет только нулевое решение, то 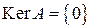 . А это, как известно, равносильно тому, что левый обратный оператор
. А это, как известно, равносильно тому, что левый обратный оператор  , находим, что
, находим, что .
.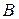 ограничен, так как
ограничен, так как 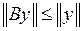 .
.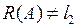 , то оператор А не является сюрьекцией. Следовательно, А необратим.
, то оператор А не является сюрьекцией. Следовательно, А необратим. .
.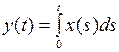 дифференцируема, причем
дифференцируема, причем 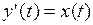 . Значит,
. Значит, 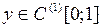 . Кроме того, очевидно, что
. Кроме того, очевидно, что 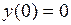 .
. . Поэтому
. Поэтому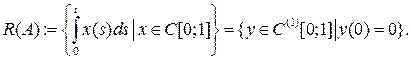
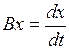 . Поскольку (снова по теореме Барроу)
. Поскольку (снова по теореме Барроу)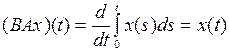
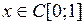 , то
, то 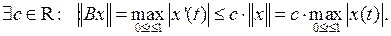
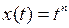
 , получаем
, получаем 
 . Противоречие.
. Противоречие. , оператор А не является сюръекцией. Следовательно, не существует
, оператор А не является сюръекцией. Следовательно, не существует 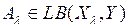 , где
, где 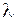 – числовой параметр,
– числовой параметр, 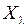 , Y − банаховы пространства. Выяснить, при каких значениях
, Y − банаховы пространства. Выяснить, при каких значениях 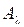 , и построить его. При каких значениях
, и построить его. При каких значениях 


