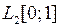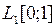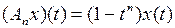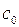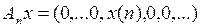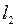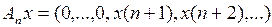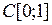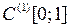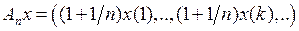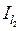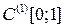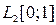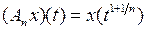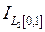Тема 3.2
Линейные ограниченные операторы в банаховых пространствах Ниже X, Y – векторные пространства над полем К (К Определение. Отображение . Определение. Пусть X, Y – нормированные пространства над полем К. Линейный оператор . При этом число С называется константой ограниченности оператора А. Определение. Пусть X, Y – нормированные пространства над полем К, Теорема. Пусть X, Y –нормированные пространства над полем К,
Теорема. Пусть X, Y – нормированные пространства над полем К, 1) оператор А непрерывен; 2) оператор А непрерывен в точке 0; 3) оператор А ограничен. Определение. Пусть X, Y – нормированные пространства над полем К. Говорят, что последовательность Сходимость по норме влечет сильную, но обратное утверждение, вообще говоря, неверно.
3.2.1. Пусть X, Y – векторные пространства. Выяснить, совпадет ли область определения Таблица 3.2.1
3.2.2. Доказать, что данный оператор А:Х Таблица 3.2.2
3.2.3. Доказать, что данный оператор А, действующий из Х в Y, является линейным ограниченным, и найти его норму (таблица 3.2.3).
Таблица 3.2.3
3.2.4. Доказать, что данный оператор взвешенного сдвига А, действующий из Х в Y, является линейным ограниченным, и найти его норму (таблица 3.2.4).
Таблица 3.2.4
3.2.5. Доказать, что данный интегральный оператор А, действующий из X в Y, является линейным ограниченным, и найти его норму (таблица 3.2.5). Таблица 3.2.5
Окончание таблицы 3.2.5
3.2.6. Для данных нормированных пространств X, Y,последовательности операторов 2) сходится ли Таблица 3.2.6
|

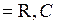 ).
). называется линейным оператором, если оно обладает следующим свойством:
называется линейным оператором, если оно обладает следующим свойством: ), если существует такое число С, что при всех х из Х выполняется неравенство ограниченности:
), если существует такое число С, что при всех х из Х выполняется неравенство ограниченности: .
. .
.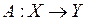 линейным оператор. Следующие утверждения равносильны:
линейным оператор. Следующие утверждения равносильны:
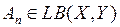 сходится по норме (сильно) к ограниченному оператору
сходится по норме (сильно) к ограниченному оператору 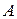 , если
, если 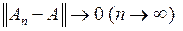 (соответственно
(соответственно 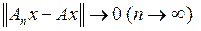 при всех х из Х).
при всех х из Х). оператора А с пространством Х. Является ли оператор А линейным оператором из
оператора А с пространством Х. Является ли оператор А линейным оператором из  в Y (таблица 3.2.1)?
в Y (таблица 3.2.1)?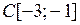
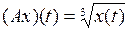
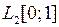

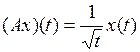

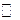
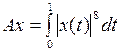
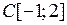

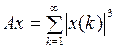




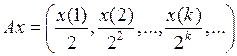

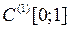
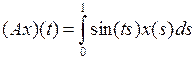
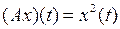
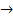 Y умножения на функциюявляется линейным ограниченным, и найти его норму (таблица 3.2.2).
Y умножения на функциюявляется линейным ограниченным, и найти его норму (таблица 3.2.2).

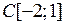
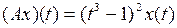
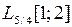
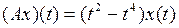

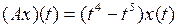
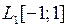
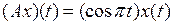
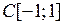

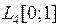
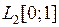
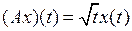
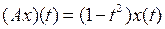
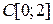
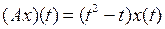

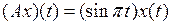

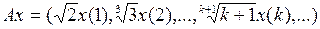
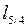
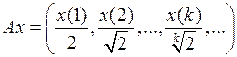

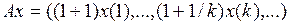

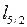
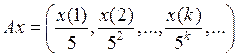
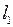
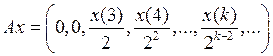

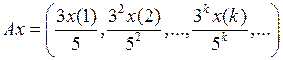
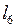


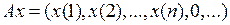


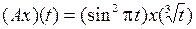
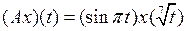


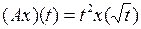
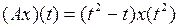
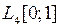

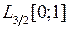
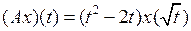
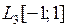
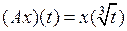
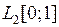

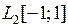

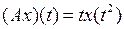

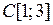
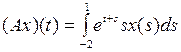

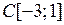
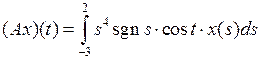
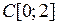
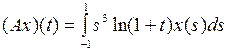
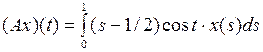
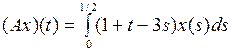

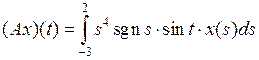

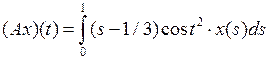
 и оператора
и оператора  поточечно (т. е. сильно) к оператору А;
поточечно (т. е. сильно) к оператору А;