Примеры решения типовых задач. 1. Является ли множество А выпуклым в пространстве Х?
1. Является ли множество А выпуклым в пространстве Х?
Пример 1.
Решение. Воспользуемся определением выпуклости. Возьмем
Значит, множество А является выпуклым.
2. Проверить, является ли заданная система векторов
Пример 1.
Решение. Покажем сначала, что для любого натурального n система
является линейно независимой. Пусть
Подставив в это равенство
Сокращая на
(Возможно другое решение: алгебраическое уравнение (2) не может иметь более n корней, если не все его коэффициенты равны нулю). Наконец, так как любая конечная подсистема нашей системы содержится в системе вида (1) при достаточно большом n, то данная бесконечная система тоже линейно независима.
Пример 2.
Решение. Заметим, что
Тогда
а значит, данные функции линейно зависимы.
3. Привести пример последовательности
Пример 1.
Решение. Рассмотрим последовательность
Допустим, что
то
Пример 2.
Решение. Рассмотрим в пространстве
Тогда в
то есть Допустим, что
Отсюда следует, что если
Пример 3.
Решение. Рассмотрим последовательность В пространстве
не стремится к нулю при
и рассуждая, как в предыдущих примерах, получим, что
4. Выяснить, являются ли нормы p и q эквивалентными в данном пространстве X.
Пример 1.
Решение. Очевидно, что
то есть
При
Полученное противоречие показывает, что нормы p и q не эквива-лентны.
Пример 2.
Решение. Заметим, что
Допустим теперь, что
Возьмем здесь
Пример 3.
Решение. Так как при всех
то С другой стороны, так как
то Итак, мы доказали, что p и q – эквивалентные нормы.
Пример 4.
Решение. В силу неравенства Коши-Буняковского
Допустим, что
Так как
что невозможно ни при каком a. Значит, нормы p и q не эквивалентны.
5. Построить изоморфизм между факторпространством L/M и одним из стандартных линейных пространств.
Пример 1.
Решение. Возьмем произвольный элемент
Это равенство показывает, что отображение
|

 .
. ,
,  и покажем, что
и покажем, что  . Действительно, так как
. Действительно, так как 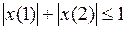 и
и  , то
, то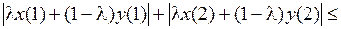

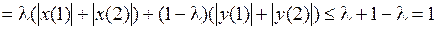 .
.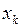 в пространстве Х линейно независимой.
в пространстве Х линейно независимой. .
. (1)
(1)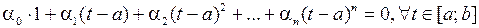 (2)
(2)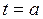 , получим
, получим  , а потому
, а потому .
.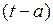 и снова полагая
и снова полагая 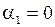 . Продолжая этот процесс, окончательно будем иметь
. Продолжая этот процесс, окончательно будем иметь .
.

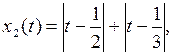
 .
. ,
,  .
. ,
,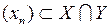 , сходящейся в Х, но не сходящейся в Y, если пространства Х и Y наделены естественными нормами.
, сходящейся в Х, но не сходящейся в Y, если пространства Х и Y наделены естественными нормами. .
. , принадлежащуюпространству
, принадлежащуюпространству 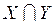 . В пространстве
. В пространстве 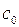 она сходится к вектору
она сходится к вектору  , так как
, так как при
при 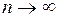 .
. . Поскольку
. Поскольку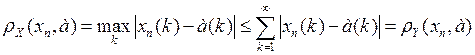 ,
,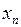 сходится к а и в пространстве
сходится к а и в пространстве  . В силу единственности предела отсюда следует, что
. В силу единственности предела отсюда следует, что  . Но этот вектор не принадлежит
. Но этот вектор не принадлежит 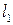 (почему?). Полученное противоречие показывает, что в
(почему?). Полученное противоречие показывает, что в 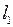 данная последовательность не сходится.
данная последовательность не сходится.
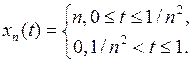
 имеем
имеем при
при  в
в  сходится в
сходится в  к некоторой точке а. В силу неравенства Коши-Буняковского имеем
к некоторой точке а. В силу неравенства Коши-Буняковского имеем .
. в
в  . Следовательно, в силу единственности предела
. Следовательно, в силу единственности предела  . С другой стороны, легко проверить, что
. С другой стороны, легко проверить, что 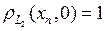 . Получили противоречие. Таким образом, в
. Получили противоречие. Таким образом, в 

 .
. имеем
имеем 
 последовательность
последовательность 
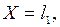



 . Допустим теперь, что
. Допустим теперь, что
 ,
,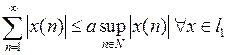 .
. последнее неравенство примет вид
последнее неравенство примет вид .
.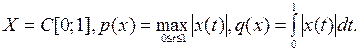

 .
.
 , то есть
, то есть .
. . Тогда последнее неравенство примет вид
. Тогда последнее неравенство примет вид  , то есть
, то есть 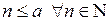 . Полученное противоречие показывает, что нормы p и q не эквивалентны.
. Полученное противоречие показывает, что нормы p и q не эквивалентны.

 .
. справедливо неравенство
справедливо неравенство ,
,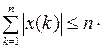
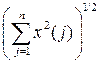 , то есть
, то есть  .
. ,
, , т.е.
, т.е.  .
.

 .
. .
.


 , то это неравенство примет вид
, то это неравенство примет вид
 ,
,
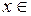 с. Его класс эквивалентности есть
с. Его класс эквивалентности есть
 .
. задаваемое формулой
задаваемое формулой  , определено корректно и является инъективным (почему?). Кроме того, оно линейно и сюръективно (проверьте это). Значит,
, определено корректно и является инъективным (почему?). Кроме того, оно линейно и сюръективно (проверьте это). Значит,  – изоморфизм линейных пространств
– изоморфизм линейных пространств  и
и  .
.


