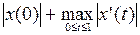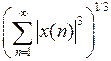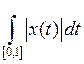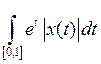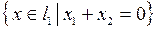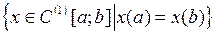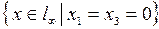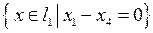Линейные нормированные пространства
Линейные нормированные пространства и
Всюду ниже Х – векторное пространство над полем К (К = Определение. Пусть
называется линейной комбинацией векторов Определение. Конечная система
возможно лишь при Определение. Бесконечная система Определение. Пусть 1) биективно; 2) линейно, т.е. удовлетворяет тождеству
Определение. Пусть
Определение. Подмножество Теорема-определение. Пусть
является векторным пространством относительно операций
Оно называется факторпространством пространства Х по подпространству М.
1) 2) 3) Часто вместо Определение. Если в предыдущем определении заменить аксиому 1) более слабой:
то получим определение полунормы. Определение. Векторное пространство Х, наделенное норомой, называется нормированным. Каждое нормированное пространство
Таким образом, к нормированным пространствам применимы все понятия и результаты теории метрических пространств. Определение. Две нормы p и q в векторном пространстве Х называются эквивалентными, если существуют такие положительные числа a и b, что при всез х из Х выполняются неравенства
3.1.1. Проверить, является ли функция p полуноромой, нормой в пространстве X (таблица 3.1.1).
Таблица 3.1.1
Окончание таблицы 3.1.1
3.1.2. Является ли множество А выпуклым в пространстве X (таблица 3.1.2)?
Таблица 3.1.2
Окончание таблицы 3.1.2
3.1.3. Проверить, является ли последовательность векторов
Таблица 3.1.3
3.1.4. Привести пример последовательности
Таблица 3.1.4
3.1.5. Являются ли нормы p и q эквивалентными в пространстве E (таблица 3.1.5)?
Таблица 3.1.5
3.1.6. Построить изоморфизм между факторпространством L/M и одним из стандартных линейных пространств (таблица 3.1.6). Таблица 3.1.6
|

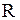 ,
,  ).
).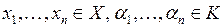 . Выражение
. Выражение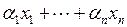
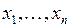 с коэффициентами
с коэффициентами 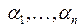 .
.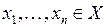 называется линейно независимой, если равенство
называется линейно независимой, если равенство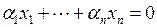
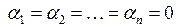 . В противном случае она называется линейно зависимой.
. В противном случае она называется линейно зависимой.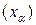 векторов из
векторов из 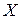 называется линейно независимой, если каждая ее конечная подсистема линейно независима.
называется линейно независимой, если каждая ее конечная подсистема линейно независима. – векторные пространства над полем К. Отображение
– векторные пространства над полем К. Отображение  называется изоморфизмом векторных пространств, если оно
называется изоморфизмом векторных пространств, если оно
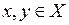 . Отрезком в Х с концами х и у называется множество
. Отрезком в Х с концами х и у называется множество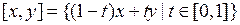 .
.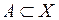 называется выпуклым, если вместе с любыми своими точками х и у оно содержит и весь отрезок [ x,y ].
называется выпуклым, если вместе с любыми своими точками х и у оно содержит и весь отрезок [ x,y ].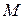 - подпространство пространства
- подпространство пространства  , состоящее из множеств вида
, состоящее из множеств вида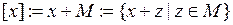 ,
,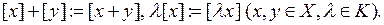
 Определение. Отображение
Определение. Отображение  называется нормой, если она обладает следующими свойствами:
называется нормой, если она обладает следующими свойствами: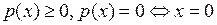 ;
;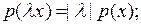
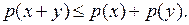
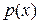 пишут
пишут 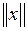 .
.
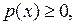
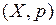 становится метрическим при наделении его естественной метрикой
становится метрическим при наделении его естественной метрикой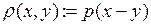 .
.







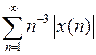
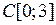
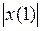
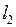

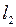
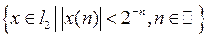
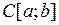
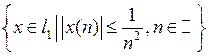
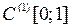
 k
k
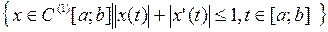
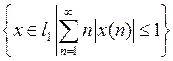

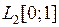
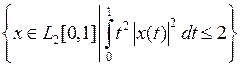
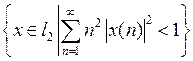
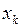 в пространстве X линейно независимой (таблица 3.1.3).
в пространстве X линейно независимой (таблица 3.1.3).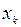
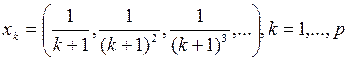
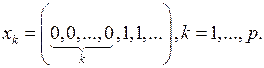


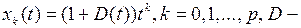 функция Дирихле
функция Дирихле


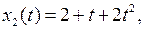
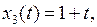
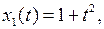

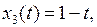
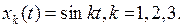
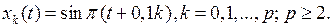
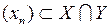 , которая сходится в X, но не сходится в Y, если пространства X и Y наделены естественными нормами (таблица 3.1.4).
, которая сходится в X, но не сходится в Y, если пространства X и Y наделены естественными нормами (таблица 3.1.4).