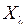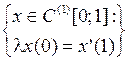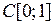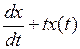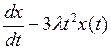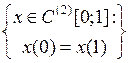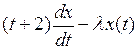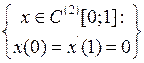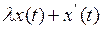Определение. Пусть X, Y – векторные пространства над полем К,  - линейный оператор. Оператор А называется обратимым, если уравнение
- линейный оператор. Оператор А называется обратимым, если уравнение
 (1)
(1)
при любом у из 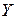 имеет единственное решение х из Х.
имеет единственное решение х из Х.
При этом отображение  , ставящее в соответствие каждому у из
, ставящее в соответствие каждому у из 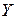 решение х уравнения (1), называется оператором, обратным к А.
решение х уравнения (1), называется оператором, обратным к А.
Оператор  имеет обратный
имеет обратный  тогда и только тогда, когда он биективен.
тогда и только тогда, когда он биективен.
Ниже 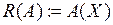 - множество значений (образ) оператора А, Ker A:=
- множество значений (образ) оператора А, Ker A:=  – ядро (множество нулей) оператора А.
– ядро (множество нулей) оператора А.
Определение. Оператор 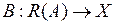 , удовлетворяющий условию ВА=IX, называется левым обратным к А.
, удовлетворяющий условию ВА=IX, называется левым обратным к А.
Лемма. ПустьX, Y – векторные пространства над К,  - линейный оператор. Следующие утверждения равносильны:
- линейный оператор. Следующие утверждения равносильны:
1) оператор А имеет левый обратный;
2) оператор А инъективен;
3)Ker A={0}.
Для нахождения левого обратного решают уравнение (1) с 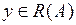
Теорема (Банаха об обратном операторе). ПустьX, Y – банаховы пространства над полем 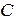 ,
,  - ограниченный линейный оператор. Если оператор А обратим, то его обратный тоже ограничен.
- ограниченный линейный оператор. Если оператор А обратим, то его обратный тоже ограничен.
3.3.1. При каких значениях параметра 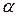 обратим данный оператор
обратим данный оператор  ? Найдите обратный оператор
? Найдите обратный оператор  , когда он существует (таблица 3.3.1).
, когда он существует (таблица 3.3.1).
Таблица 3.3.1
Окончание таблицы 3.3.1
3.3.2. Пусть 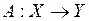 . Доказать, что существует непрерывный обратный оператор
. Доказать, что существует непрерывный обратный оператор  , и построить его (таблица 3.3.2).
, и построить его (таблица 3.3.2).
Таблица 3.3.2
Окончание таблицы 3.3.2
3.3.3. Пусть 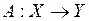 .
.
1) Что представляет собой множество значений 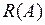 оператора А?
оператора А?
2) Существует ли на 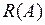 левый обратный оператор
левый обратный оператор  ?
?
3) Является ли оператор 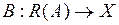 ограниченным, если он существует?
ограниченным, если он существует?
4) Существует ли обратный оператор 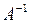 (таблица 3.3.3)?
(таблица 3.3.3)?
Таблица 3.3.3
Окончание таблицы 3.3.3
3.3.4 Пусть 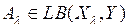 , где
, где 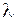 – числовой параметр,
– числовой параметр, 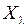 , Y − банаховы пространства. Выяснить, при каких значениях
, Y − банаховы пространства. Выяснить, при каких значениях 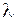 существует обратный оператор к оператору
существует обратный оператор к оператору 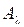 , и построить его. При каких значениях
, и построить его. При каких значениях 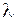 оператор
оператор 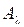 непрерывно обратим? (таблица 3.3.4)?
непрерывно обратим? (таблица 3.3.4)?
Таблица 3.3.4
Окончание таблицы 3.3.4

 - линейный оператор. Оператор А называется обратимым, если уравнение
- линейный оператор. Оператор А называется обратимым, если уравнение (1)
(1)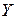 имеет единственное решение х из Х.
имеет единственное решение х из Х. , ставящее в соответствие каждому у из
, ставящее в соответствие каждому у из 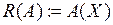 - множество значений (образ) оператора А, Ker A:=
- множество значений (образ) оператора А, Ker A:=  – ядро (множество нулей) оператора А.
– ядро (множество нулей) оператора А.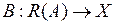 , удовлетворяющий условию ВА=IX, называется левым обратным к А.
, удовлетворяющий условию ВА=IX, называется левым обратным к А.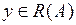
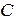 ,
, 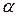 обратим данный оператор
обратим данный оператор  ? Найдите обратный оператор
? Найдите обратный оператор  , когда он существует (таблица 3.3.1).
, когда он существует (таблица 3.3.1).


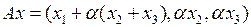
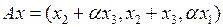
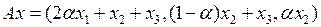
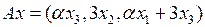

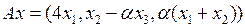

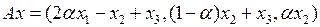
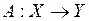 . Доказать, что существует непрерывный обратный оператор
. Доказать, что существует непрерывный обратный оператор 
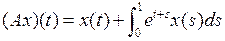
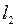
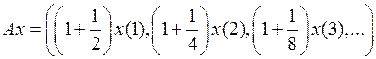



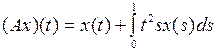
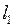
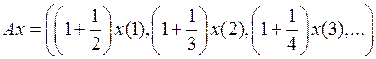
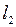
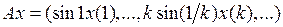
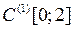

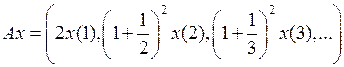
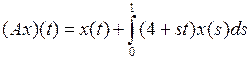
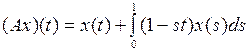
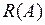 оператора А?
оператора А? ?
?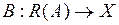 ограниченным, если он существует?
ограниченным, если он существует?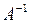 (таблица 3.3.3)?
(таблица 3.3.3)?
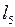
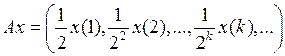
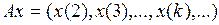
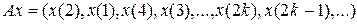

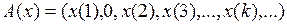

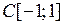
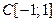

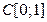


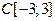

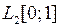
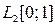
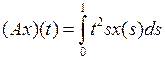

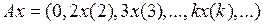
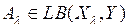 , где
, где 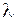 – числовой параметр,
– числовой параметр, 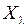 , Y − банаховы пространства. Выяснить, при каких значениях
, Y − банаховы пространства. Выяснить, при каких значениях 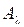 , и построить его. При каких значениях
, и построить его. При каких значениях