Примеры решения типовых задач. 1.Пусть X, Y – векторные пространства
1. Пусть X, Y – векторные пространства. Выяснить, совпадет ли область определения Пример 1.
Решение. Если
Отсюда следует, что Оператор А не является линейным (рассмотрите, например, Хотя это и не требуется по условию задачи, исследуем оператор А на непрерывность. Для любой точки
(мы воспользовались числовым неравенством Пример 2.
Решение. В этом примере Очевидно, A является линейным оператором (проверьте). Хотя это и не требуется по условию задачи, исследуем оператор А на непрерывность, что равносильно исследованию его ограниченности. Докажем, что A не является ограниченным. Допустим противное, т.е. что
Поскольку частичные суммы гармонического ряда
Пример 3.
Решение. Пусть
показывает, что Легко проверить, что А линеен (проверьте). Докажем, что А ограничен. Используя предыдущее неравенство, получаем
Наконец, как известно, из ограниченности оператора А следуетего непрерывность.
Пример 4.
Решение. Здесь
Тогда
В то же время,
Таким образом, из того, что
Пример 5.
Решение. Очевидно, что
То есть из того, что
2. Доказать, что оператор
а) Оператор умножения на функцию, действующий из X в Y.
Пример 1.
Решение. Ясно, что A − линейный оператор (проверьте). Далее, так как
то A ограничен с константой ограниченности Докажем теперь противоположное неравенство, т. е. что
Теперь из формулы Сопоставляя полученные неравенства, заключаем, что
б) Оператор, действующий из
Пример 1.
Решение. Ясно, что A − линейный оператор. Так как
то оператор A ограничен, причем С другой стороны, для точки Из полученных неравенств следует, что
|

 оператора А с пространством Х. Является ли оператор А линейным оператором из
оператора А с пространством Х. Является ли оператор А линейным оператором из  в Y?
в Y? .
. , то
, то  =
= 
 . Поэтому в силу неравенства Коши-Буняковского
. Поэтому в силу неравенства Коши-Буняковского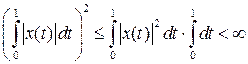 . (1)
. (1) . Таким образом,
. Таким образом,  .
. ).
). оценим расстояние
оценим расстояние

 , а затем неравенством (1)). Поэтому для любого
, а затем неравенством (1)). Поэтому для любого  получаем при
получаем при  что для любого
что для любого  из неравенства
из неравенства  следует неравенство
следует неравенство  . Стало быть, оператор A непрерывен на
. Стало быть, оператор A непрерывен на 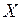 .
. .
.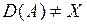 , так как, например,
, так как, например,  , но
, но  (в обоих случаях сходимость соответствующего ряда исследуется с помощью интегрального признака; докажите это).
(в обоих случаях сходимость соответствующего ряда исследуется с помощью интегрального признака; докажите это).
 . Полагая в последнем неравенстве
. Полагая в последнем неравенстве  , получаем
, получаем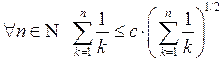 , т.е.
, т.е. 
 .
. не являются ограниченными, мы пришли к противоречию. Значит, оператор A не является непрерывным.
не являются ограниченными, мы пришли к противоречию. Значит, оператор A не является непрерывным. .
. (тогда
(тогда  ). Оценка
). Оценка
 ,
, . Значит,
. Значит, 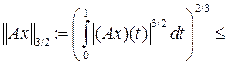
 .
.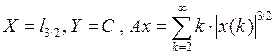 .
. принадлежит Х, но
принадлежит Х, но  . Далее, оператор A не является линейным (как в примере 1). Докажем, что он не является непрерывным. Действительно, возьмём следующую последовательность
. Далее, оператор A не является линейным (как в примере 1). Докажем, что он не является непрерывным. Действительно, возьмём следующую последовательность  точек из
точек из  :
: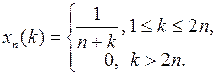
 в
в  при
при  .
.
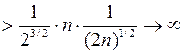 .
. , не следует, что
, не следует, что  . Мы показали, что А не является непрерывным в нуле, значит, A не является непрерывным на
. Мы показали, что А не является непрерывным в нуле, значит, A не является непрерывным на  .
. точек пространства
точек пространства  . Она сходится к 0, так как
. Она сходится к 0, так как 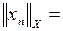
 при
при  при
при  . Таким образом, оператор A не является непрерывным на
. Таким образом, оператор A не является непрерывным на  является линейным ограниченным, и найти его норму.
является линейным ограниченным, и найти его норму. .
.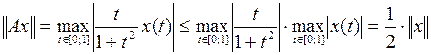 , (2)
, (2) . А поскольку норма оператора есть наименьшая из констант ограниченности, то
. А поскольку норма оператора есть наименьшая из констант ограниченности, то  .
.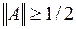 . Для этого постараемся подобрать такой ненулевой вектор
. Для этого постараемся подобрать такой ненулевой вектор  , для которого неравенство (2) превращается в равенство.Возьмём
, для которого неравенство (2) превращается в равенство.Возьмём 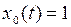 . Тогда, как легко подсчитать,
. Тогда, как легко подсчитать, .
. следует, что
следует, что  .
. .
. в
в  .
. ,
, имеем
имеем  . Значит,
. Значит, 


