Виды дисперсионного анализа
ствах массовой информации и др.) на число посетителей в кинотеатре? Пример постановки вопроса двухфакторного дисперсионного анализа (см. табл. 1.3): влияет ли регион и тип упаковки на объем продаж определенного товара? Пример постановки вопроса многомерного дисперсионного анализа: влияют ли регион и тип упаковки на объем продаж и число жалоб потребителей определенного товара? В основе техники проведения дисперсионного анализа лежит сравнение средних величин в разных группах. Например, для того чтобы определить, влияет ли пол студента на успеваемость, необходимо сравнить среднюю успеваемость юношей и девушек. Если средняя успеваемость девушек отличается от средней успеваемости юношей, то можно утверждать, что пол студента влияет на успеваемость, и наоборот. Приведенный пример сравнения средних величин в двух группах (юношей и девушек) осуществляется при помощи Т-теста. Т-тест является частным случаем дисперсионного анализа, в ходе которого осуществляется сравнение средних величин в нескольких группах. Свое название дисперсионный анализ получил благодаря одному из условий сравнения средних величин в разных группах: дисперсии исследуемых величин в разных группах должны быть равны. Дисперсия — показатель, характеризующий рассеяние значений количественного признака вокруг своего среднего значения. Подробно техника сравнения средних величин будет рассмотрена в главе 3 «Сравнение средних величин в SPSS». КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Чем обусловливается необходимость использования статистической выборки при проведении масштабных маркетинговых исследований? 2. В чем заключается основное требование, предъявляемое к статистической выборке? 3. Назовите основные методы формирования статистической выборки, их достоинства и недостатки. 4. Какие виды статистической выборки отличаются наиболее высокой степенью репрезентативности и почему? 5. Назовите основные задачи, решаемые в ходе формирования статистической выборки. 6. Назовите основные методы статистического анализа, применяемые в маркетинговых исследованиях, и их виды. 7. Назовите методы статистического анализа, при помощи которых можно найти ответы на следующие вопросы: а) влияет ли цвет упаковки товара и место его расположения в торговом зале на объем продаж; б) возможно ли разделить постоянных клиентов магазина на группы, используя в качестве критериев разделения объемы совершаемых покупок и частоту посещения магазина; в) насколько увеличится объем продаж товара при увеличении расходов на рекламу на 10% при условии постоянства цены на данный товар; г) по каким социально-демографическим признакам отличаются люди, приобретающие и не приобретающие товар X. 2. ФОРМИРОВАНИЕ ИСХОДНОЙ БАЗЫ ДАННЫХ В SPSS 2.1. СТРУКТУРА РЕДАКТОРА ДАННЫХ Файл исходной базы данных для проведения статистического анализа в SPSS формируется в редакторе данных (Data Editor). Редактор данных имеет две вкладки: «Свойства переменных» (Variable View) и «Значения переменных» (Date View). Данные вкладки представляют собой таблицы, содержащие информацию о данных, собранных для проведения анализа. Во вкладке «Variable View» представлена таблица с данными, описывающими свойства переменных. Каждая строка отображает переменную (вопрос анкеты), каждый столбец — ее свойства (рис. 2.1). В столбце «Name» таблицы «Свойства переменных» указывается имя переменной — как правило, это номер вопроса в анкете. Например, в базе данных, представленной в табл. 2.1, переменная «пол» имеет название «s_l», поскольку в разделе анкеты «социально-демографические признаки» вопрос о поле респондента находился на первом месте. Имена переменных могут содержать буквы латинского алфавита и цифры, а также некоторые символы: $, #. В сумме число знаков не должно превышать «8». Не допускаются пробелы и буквы других алфавитов. Имя переменной должно начинаться с буквы и не может заканчиваться знаком подчеркивания «__». В столбце «Туре» таблицы «Свойства переменных» указывается тип переменной; новые, созданные, переменные по умолчанию являются числовыми (Numeric). Если требуется изменить тип переменной, следует подвести курсор в соответствующую ячейку таблицы, и при нажатии кнопки мыши на экране появится диалоговое окно «Тип переменной» (Van ible Type) (рис. 2.2).
В диалоговом окне «Тип переменной» возможен выбор формата записи значений переменной: Comma (например: 43,675.67); Dot (например: 43.675,67); Scientific notation (например: 43Е+0,4); Dollar (например: $43,675). Аналогичным образом можно выбрать текстовую переменную (Stri ig). Однако применение текстовых переменных в SPSS практически невозможно, поскольку с ними нельзя производить никаких арифметических операций и рассчитывать какие-либо статистические показатели. В поле «Width» диалогового окна «Тип переменной» (см. рис. 2.2) указывается число знаков, используемых для кодировки переменной. Например, для кодировки переменной «пол» используется только один знак («1» — «мужчины» или «2» — «женщины»). Число знаков, используемых для кодировки переменной, можно также указать в столбце «Width» («Формат столбца») таблицы «Свойства переменных» (см. табл. 2.1). В поле «Decimal Places» диалогового окна «Тип переменной» указывается число знаков после запятой при записи значений переменной. Например, для переменной «пол» в поле «Decimal Places» указывается значение 0. Ответы респондентов в данном случае заносятся в базу данных в виде целых чисел («1» — «мужчины» или «2» — «женщины»). Число знаков после запятой при записи значений переменной можно также указать в столбце «Decimals» («Десятичные разряды») таблицы «Свойства переменных». В столбце «Label» таблицы «Свойства переменных» указываются метки переменных. Метка — название, позволяющее описать переменную более подробно, чем имя переменной, она может содержать до 256 символов. В качестве этих символов могут выступагь также буквы русского алфавита. При задании меток переменных часто используются формулировки вопросов, содержащихся в анкете. Например, в качестве метки переменной «пол» в редакторе данных может быть введена фраза: «Укажите, пожалуйста, свой пол». Однако следует помнить, что метка переменной будет отображаться во всех графиках и таблицах, представляющих результаты статистического анализа. Поэтому рекомендуется использовать более лаконичные метки для наглядности представления результатов анализа. В столбце «Values» таблицы «Свойства переменных» (см. рис. 2.1) отображаются значения меток переменных. Если в поле «Label» указывается вопрос анкеты, то в поле «Values» указываются коды возможных вариантов ответа на этот вопрос. Для заполнения поля «Values» необходимо произвести кодировку вариантов отьета. При подведении курсора к соответствующей ячейке таблицы и нажатии клавиши мыши на экране компьютера появляется диалоговое окно «Значение меток переменных» (Value Labels) (рис. 2.3). В диалоговом окне «Значение меток переменных» в поле «Value» указываются числовые коды вариантов ответа, а в поле «Value Label» — их вербальные форму- лировки. При задании вербальных формулировок следует учитывать, что они будут фигурировать впоследствии в графиках и анапити-
ческих таблицах. Например, ответ на вопрос о половой принадлежности респондента должен быть не «мужской» («женский»), а «мужчины» («женщины»). Процедура кодировки производится поэтапно по каждому варианту ответа. В рассматриваемом примере кодировки переменной «пол», сначала в поле «Value» указывается числовой код «1», а в поле «Value Label» — вербальный вариант ответа «мужчины». После нажатия кнопки «Ada» эти данные переносятся в большое поле диалогового окна «Значение меток переменных». Затем подобным образом кодируется вариант ответа «женщины». После нажатия кнопки «ОК» диалоговое окно «Значение меток переменных» закрывается, а указанные в нем данные заносятся в столбец «Values» таблицы «Свойства переменных». В столбце «Missing»(«Пропущенные значения») рис. 2.1 «Свойства переменных» следует указать, какие коды вариантов ответов следует исключить из анализа. В SPSS допускаются два вида пропущенных значений: • Пропущенные значения, определяемые системой (System- defined m»ssirig values). Если в матрице данных есть незаполненные ячейки, система SPSS самостоятельно идент ифицирует их как пропущенные значения. Отсутствие ответа отражается в исходном файле данных в виде запятой. • Пропущенные ответы, задаваемые пользователем (User-defined missing values). Например, среди вариантов ответа на поставленный вопрос можно закодировать отсутствие определенного ответа («98» — «не знаю», «99» — «нет данных») и затем в поле «Ми и ig» указать эти коды, чтобы исключить соответствующие варианты ответа из анализируемых данных. При подведении курсора к соответствующей ячейке столбца «Мissing» и нажатии кнопки мыши открывается диалоговое окно «Пропущенные значения» (рис. 2.4). По умолчанию в диалоговом окне «Пропущенные значения» отмечается команда «No missing values». Это означает, что пропущенных значений нет, а все варианты ответа на вопрос рассматриваются как допустимые. Если бы нужно было указать коды вариантов ответа, исключаемых из процедуры анализа, то следовало бы выбрать команду «Discrete missing values» и в соответствующих ячейках указать коды «98» и «99» («98» — «не знаю», «99» — «нет данных»). Для одной переменной можно задать до трех пропущенных значений.
Существует еще один вариант задания пропущенных значений: «Range plus one optional discrete missing value» («Диапазон плюс единичное пропущенное значение»). Эта команда применялась бы в случае, если бы, например, при заданных значениях переменной «возраст» нужно было бы исключить из исследований респондентов от 20 до 40 лет, а также лиц в возрасте 55 лет. В рассматриваемом примере описания свойств переменной «пол» достаточно сложно представить, чтобы кто-то из респондентов затруднился ответить или не захотел отвечать на вопрос о своей половой принадлежности. Поэтому в поле «Missing» таблицы «Свойства переменных» отсутствуют какие-либо коды вариантов ответа. В столбце «Columns»(«Столбцы») таблицы «Свойства переменных» указывается ширина столбца, содержащего значения соответствующей переменной в таблице другой вкладки редактора данных: «Значения переменных» (Date View) (рис. 2.5). По умолчанию ширина столбца задается «8». В столбце «Alignment» («Выравнивание») таблицы «Свойства переменных» задается положение кодов ответов в таблице «Значения переменных» во вкладке редактора данных «Date View». Они могут быть выровнены по правому краю (Right), по левому краю (Left) или по центру (Center). По умолчанию задается выравнивание по правому краю. Если нужно изменить порядок выравнивания, то следует подвести курсор к соответствующей ячейке столбца «Alignment», и при нажатии клавиши мыши на экране появится меню, содержащее три вышеперечисленных варианта выравнивания данных, из которых следует выбрать желаемый.
В столбце «Measure» («Шкала измерения») таблицы «Свойства переменных» указывается тип шкалы, по которой измеряется переменная. По умолчанию задается метрическая шкала (Scale). В случае необходимости тип шкалы можно изменить. Для этого следует подвести курсор в соответствующую ячейку столбца «Measure» и нажать клавишу мыши, после чего на экране появится меню из трех типов шкалы измерения (рис. 2.6).
В зависимости от вида переменной следует выбрать один из трех типов шкалы измерения: метрическую (Scale), порядковую (Ordinal) или номинальную (Nominal). Поскольку переменная «пол» измеряется по номинальной шкале, то при заполнении таблицы «Свойства переменных» в строке этой переменной в столбце «Measure» выбирается тип шкалы измерения «Nominal». (Более подробно этот вопрос будет рассмотрен в подразделе 2.3 «Типы шкал измерения переменных».) После того как заполнена таблица «Свойства переменных» во вкладке редактора данных «Variable View», следует открыть другую вкладку редактора данных — «Date View». Во вкладке редактора данных «Date View» представлена таблица с данными, описывающими значения переменных. Каждый столбец отображает переменную (вопрос анкеты), каждая строка — отдельное наблюдение (объект сбора информации) (см. рис. 2.5). В качестве объектов сбора информации могут выступать люди, предприятия, продукты, бренды и т.д. На рис. 2.5 представлен фрагмент таблицы, содержащей значения переменных, описанных в таблице «Свойства переменных». Из данных таблицы «Свойства переменных» (см. табл. 2.1) известно, что переменная с именем «s_l» имеет метку «Пол». Метка переменной «пол» имеет два значения: «мужчины» (код «1») и женщины (код «2»). В столбце «s _1» таблицы «Значения переменных» (см. рис. 2.5) содержатся закодированные ответы респондентов на вопрос об их половой принадлежности: «1» или «2». Так, по данным этой таблицы известно, что респондент в строке 1143 — мужчина, а респондент в строке 1144 — женщина. Из данных таблицы «Свойства переменных» также известно, что переменная с именем «s _1а» имеет метку «Возраст». Эта переменная не имеет кодировки (в столбце «Values» отсутствуют значения меток переменных). В столбце «s,1а» таблицы «Значения переменных» содержатся незакодированные ответы респондентов на вопрос об их возрасте. Так, по данным этой таблицы известно, что респондент в строке 1143 — мужчина в возрасте 31 года, а респондент в строке 1144 — женщина в возрасте 33 лет. 2.2. ВИДЫ КОДИРОВКИ В SPSS существует два основных вида кодировки данных: категориальная и дихотомическая. Категориальная кодировка предполагает несколько вариантов ответа на поставленный вопрос, т.е. метка переменной может принимать несколько значений. Дихотомическая кодировка предполагает только два варианта ответа на поставленный вопрос, т.е. метка переменной может принимать только два значения («да» или «нет»). Вид кодировки переменных определяется типом вопроса анкеты. Вопросы бывают открытые (без заданных вариантов ответа) и закрытые (с заданными вариантами ответа). Закрытые вопросы, в свою очередь, бывают одновариантные (альтернативные) и многовариантные (безальтернативные). Одновариантные (альтернативные) вопросы предполагают возможность выбора только одного из предложенных вариантов ответа. Многовариантные (безальтернативные) вопросы предоставляют возможность выбрать несколько из предложенных вариантов ответа. Основное правило создания исходного файла данных в SPSS состоит в том, что создаваемые переменные должны быть однова- риантными, т.е. одна переменная должна иметь одну метку. В этой связи при занесении в файл SPSS данных по ответам на один многовариантный вопрос создается несколько однояариантных переменных. При занесении в файл SPSS данных по одновариантному вопросу создается одна пепеменная, имеющая одну метку. Метка создаваемой переменной может иметь несколько значений. В этом случае применяется категориальная кодировка данных (табл. 2.1).
При использовании категориальной кодировки данных все респонденты, участвующие в исследовании, могут быть поделены на категории относительно выбранного ими варианта ответа. Например, относительно приобретаемого продукта все респонденты могут быть поделены на три категории: «приобретающие продукт Л», «приобретающие продукт В» и «приобретающие продукт С». При занесении в файл UPSS данных по многовариантному вопросу создается несколько переменных, каждая переменная имеет свою метку. Метки создаваемых переменных могут иметь только два значения. В этом случае применяется дихотомическая кодировка данных (табл. 2.2).
В рис. 2.7 и 2.8 представлены фрагменты вкладок редактора данных «Variable View» и «Data V iew», которые иллюстрируют представление в исходном файле данных SPSS одного многовариантного вопроса в виде нескольких одновариантных переменных.
В рассматриваемом примере (см. рис. 2.7,2.8) представлены данные о туристах, отдыхающих в курортной зоне Восточной Баварии «Баварский лес». Эти данные содержат ответы на вопрос анкеты № 33: «Каким спортом Вы занимаетесь на отдыхе?» В качестве возможных вариантов ответа на этот вопрос предлагаются 14 видов спортивных занятий, наиболее популярных в Восточной Баварии: «туристические походы», «велосипедный спорт», «плавание в природных водоемах», «плавание в бассейне» и т.д. Респонденты могут выбрать несколько из предлагаемых вариантов ответов. Как видно из данных, представленных в табл. 2.S, вопрос анкеты № 33 представлен в файле данных SPSS в виде 14 одновари- антных переменных с именами «q_33_l», «q_33 2»... «q_33_14». Каждая переменная имеет собственную метку, обозначающую вид спортивного занятия: «Походы», «Велосипедный спорт»... «Ролики». Все 14 переменных имеют дихотомическую кодировку ответов. Каждая мегха переменной имеет четыре значения (см. рис. 2.7). два их которых («98» — «не знаю», «99» — «нет данных») исключа
ются. Коды этих значений меток переменных указаны в столбце «Missing» как пропущенные данные. Значимыми для проведения исследования являются только два варианта ответа: «да» и «нет», которые указывают на то, занимается ли респондент соответствующим видом спорта. По данным фрагмента вкладки редактора данных «Data View», представленного на рис. 2.8, респондент в строке 793 совершает туристические походы, плавает только в бассейне и делает пробежки, поскольку переменные «q_33__l», «q_334» и «q_33_8» имеют положительный ответ («1» — «да»). Среди закодированных вариантов ответов встречаются цифры «98» и «99». Они обозначают, что респондент затруднился или не захотел отвечать на поставленный вопрос (см. рис. 2.8). Этим данным присваивается значение «user missing». Они исключаются из исследований по заданным условиям (столбец «Missing», рис. 2.7). Некоторые ячейки таблицы, представленной на рис. 2.8, оказались пустыми. Данным вариантам ответа присваивается значение «system missing». Это данные, которые должны были присутствовать, но их не оказалось в базе данных в связи с причинами случайного характера. Такие данные автоматически исключаются из исследований. Обобщая вышеизложенное, следует еще раз отметить, что многовариантные вопросы представляются в файле данных SPSS в виде нескольких переменных, каждая из которых представляет собой возможный вариант ответа. Однако возможны случаи, когда одновариантный вопрос представляется в виде двух переменных в файле данных SPSS. Такое возможно в случае применения так называемой двойной записи. Применение двойной записи проиллюстрировано на рис. 2.9 и 2.10. В этих таблицах представлены фрагменты файла данных SPSS, содержащего информацию о туристах, отдыхающих в курортной зоне Восточной Баварии «Баварский лес». Ряд вопросов анкеты представлен в файле данных в виде двух переменных: • Вопрос № 45: «Какую сумму Вы тратите в целом на отдых?» • Вопрос № 46: «Какую сумму Вы тратите на крупные покупки одежда, обувь, спортивный инвентарь и т.п.) во время отдыха?» • Вопрос № 47: «Какую сумму Вы тратите на проживание в гостинице/пансионе (включая обслуживание) во время отдыха?» • Вопрос № 48: «Какую сумму Вы тратите на питание (посещение кафе и ресторанов, покупки продуктов в магазине) во время отдыха?» Вопрос анкеты № 45 представлен в файле данных в виде двух переменных с именами «q_45_l» и «q_45_2» (см. рис. 2.9). Обе переменные имеют одинаковую метку «Общие расходы на отдых». Переменная с именем «q_4f _1» имеет три значения метки
переменной: «1» — «сумма в евро», «98» — «не знаю», «99» — нет данных. Переменная с именем «q_45_2» не имеет значений метки переменной (в столбце «Label» стоит отметка «None») (см. рис. 2.7). На рис. 2.10 представлен фрагмент файла данных SPSS во вкладке редакгора данных «Data View». В столбцах таблицы «Значения переменных» (Data View) представлены ответы респондентов на вопросы анкеты № 45, 46, 47 и 48. Например, если в определенной строке в столбце «q_45_1» стоит числовой код «1», это означает, что респондент назвал определенную сумму, которую он тратит на проведение отдыха. В этой же строке в столбце «q_45_2» указывается названная сумма. Двойная запись данных применяется в том случае, если необходима обработка очень большого объема информации. В рассматриваемом примере исходный файл данных SPSS был создан на базе проведения опроса туристов, отдыхающих в курортной зоне «Баварский лес», в ходе которого было опрошено 6396 респондентов. Каждый из респондентов в качестве ответа о размерах своих расходов во время проведения отпуска мог назвать шестизначное число (см рис. 2.9: в столбце «Width» отметка «6»). Порядок кодировки переменных определяется типом шкалы их измерения. Типы шкал измерения переменных подробно рассматриваются в следующем разделе. 2.3. ТИПЫ ШКАЛ ИЗМЕРЕНИЯ ПЕРЕМЕННЫХ Для работы с данными в SPSS важно знать, по шкале какого типа измеряются исследуемые переменные. Это необходимо для выбора метода анализа данных и определения возможности расчета статистических показателей (табл. 2.3). Существует четыре типа шкал измерения переменных: 1. Номинальная шкала. 2. Порядковая шкала. 3. Интервальная шкала.
4. Относительная шкала.
Номинальная шкала характеризуется самым низким уровнем измерения переменных. Все значения переменной, измеряемой по номинальной шкале, находятся на одном уровне. По этой шкале измеряются, как правило, качественные характеристики объекта исследования. Между значениями переменной, измеряемой по номинальной шкале, не существует логического порядка. Например, в качестве ответа на вопрос анкеты: «Какого производителя продукта «X» вы предпочитаете?» — может быть предложено несколько вариантов: «Производитель А», «Производитель В», «Производитель С» и т.д. В этом случае, с точки зрения исследователей, все предложенные производители являются равнозначными. Числовые коды («1», «2», «3»...) могут присваиваться значениям метки переменной в любом порядке. Переменные, измеряемые по номинальной шкале и имеющие всего два значения (например, «мужчины» и «женщины»), называются дихотомическими. Порядковая шкала является второй по уровню измерения переменных. Значения переменной, измеряемой по порядковой шкале, не являются равнозначными, они находятся на равных уровнях по отношению друг к другу и подчиняются логическому числовому порядку. Порядковая шкала характеризуется низким уровнем измерения переменных, поскольку является шкалой с неравными интервальными отрезками. Совершенно четко можно утверждать, что уровень обслуживания авиапассажиров первого класса выше, чем бизнес-класса, но насколько именно, неизвестно. Также разница в обслуживании между первым и бизнес-клас- сом, между бизнес- и эконом-классом может быть различной (см. табл. 2.3). Низкий уровень измерения переменных по порядковой шкале можно проиллюстрировать на примере переменной «Категории потребителей по уровню дохода». Потребители примерно с одинаковым уровнем дохода (например, 950 и 1050 евро) оказываются в разных категориях, а потребители с существенной разницей по уровню дохода (например, 1050 и 2950 евро) оказываются в одной категории. Интервальная шкала является третьей по уровню измерения переменных. В отличие от порядковой шкалы она является шкалой с равными интервальными отрезками. Это позволяет осуществлять количественное сравнение значений переменной, т.е. можно определить, насколько одно значение больше или меньше (лучше или хуже, длиннее или короче и т.д.) другого. Характерной чертой интервальной шкалы является отсутствие «естественного нуля», т.е. исходная точка измерения является относительной. Примерами интервальной шкалы являются шкала Цельсия и календарь. По шкале Цельсия за «0» принята температура замерзания воды, однако за «0» можно было принять любую другую температуру. Существуют также различные календари с одинаковым количеством дней в году, но разным временем начала года. В маркетинговых исследованиях очень часто используется рейтинговая шкала, когда респондентам предлагается оценить по балльной шкале (например, от 1 до 7 баллов) утверждение, продукт, бренд и т.п. Строго говоря, рейтинговая шкала является порядковой, поскольку балльные оценки субъективны. Одинаковые балльные оценки в действительности отображают разный уровень измеряемой переменной. Например, студенты, получившие одинаковые оценки на экзамене, в действительности могут иметь разный уровень знаний. Очень часто при проведении исследований шкала бапльных оценок рассматривается как интервальная. В основе этого лежит предположение, что интервальные отрезки шкалы балльных оценок одинаковы. Это дает возможность рассчитать соеднее значение переменной (например, средний балл успеваемости студентов). Расчет средней величины (среднеарифметической) для показателя, измеряемого по порядковой шкале, невозможен. Например, не существует показателя «средний класс» полета (см. табл. 2.3). Относительная шкала характеризуется самым высоким уровнем измерения переменных. Ее основное отличие от интервальной шкалы заключается в существовании «естественного нуля», который можно интерпретировать как отсутствие значения переменной. Например, если заработная плата равна нулю, это значит, что ее не выплачивают. По относительной шкале измеряются количественные характеристики. Это могут быть как физические характеристики (объем, вес, скорость и пр.), так и экономические характеристики (доход, издержки, цена и пр.). Относительная шкала получила свое название благодаря возможности сравнения значений переменной по отношению друг к другу, что невозможно при использовании интервальной шкалы измерения. Например, нельзя сказать, что человек, у которого коэффициент интеллекта (iQ) равен 160, в два раза умнее человека у которого этот показатель составляет 80. Но можно сказать, что заработная плата 1000 евро в два раза больше заработной платы 2000 евро. При выборе типа шкалы измерения переменных в SPSS (столбец «Measure» во вкладке редактора данных «Variable View») интервальная шкала и шкала отношений объединяются в один вид — метрическую шкалу (Scale). При построении в SPSS интерактивных графиков номинальная (Nominal) и порядковая (Ordinal) шкалы объединяются в «категориальный» тип (табл. 2.4).
Чем выше уровень измерения переменной, тем богаче ее информационная содержательность и тем больше возможностей осуществления расчетов и определения статистических показателей. Числовые коды («1», «2», «3»...) значений метки переменной, измеряемой по номинальной или порядковой шкале, не могут рассматриваться как числа, они представляют собой лишь некие числовые символы. Поскольку они не являются числами, с ними нельзя производить никаких арифметических операций (сложение, вычитание, деление, умножение). Что касается статистических показателей, характеризующих распределение величины, измеряемой по номинальной шкале, можно провести частотный анализ (Frequencies) и определить моду (Mode). Частоты показывают, например, сколько респондентов предпочитают того или иного производителя продукта «Л». Мода обозначает самую многочисленную группу респондентов, предпочитающих определенного производителя продукта «Л». Для переменных, измеряемых по порядковой шкале, кроме вышеуказанных статистических показателей можно определить медиану и средневзвешенное. Значения меток переменной, измеряемой по интервальной шкале, рассматриваются как числа. С ними можно производить такие арифметические операции, как сложение и вычитание. Что касается возможности расчета статистических показателей, характеризующих распределение переменной, измеряемой по интервальной шкале, кроме моды и медианы можно также определить стандартное отклонение (Std. deviation) и среднеарифметическое (Mean). (Средневзвешенное значение переменных с интервальной шкалой равно среднему арифметическому.) При расчете статистических показателей, характеризующих распределение переменной, измеряемой по интервальной шкале, не рассчитывается такой показатель, как сумма (Sum). Например, не рассчитывается «суммарный коэффициент интеллекта» для группы студентов, такого показателя не существует. Значения меток переменной, измеряемой по шкале отношений, выражаются в числах, с ними можно производить любые арифметические операции. Также можно определять любые статистические показатели, характеризующие распределение переменной. Возможна трансформация имеющихся данных, измеряемых по шкале более высокого уровня, в данные, измеряемые по шкале более низкого уровня, но не наоборот. Например, значения переменной «Уровень дохода», измеряемой по относительной шкале, можно трансформировать в значения переменной «Категории потребителей по уровню дохода», измеряемой по порядковой шкале (см. табл. 2.3). Подобная трансформация данных, производимая в целях упрощения процедуры анализа и наглядности представления результатов, неизбежно связана с частичной потерей информации и снижением точности расчетов. На практике, в том числе при применении SPSS, различие между переменными, измеряемыми по интервальной и относительной шкалам, обычно несущественно. Во многих учебниках по SPSS метрические переменные (Scale) определяются как интервальные. ип шкалы измерения переменных определяет возможность применения того или иного метода анализа данных. Все методы статистического анализа делятся на две группы: 1) методы оценки связи между переменными; 2) методы выявления структуры данных. Методы выявления структуры данных характеризуются тем, что исходные данные для проведения анализа не содержат информации (предположений) о существовании взаимосвязей между исследуемыми переменными. К таким методам относятся, например, кластерный и факторный анализ. Методы оценки связи между переменными устанавливают влияние одной или нескольких независимых переменных на одну или несколько зависимых переменных. С точки зрения теории статистики существуют правила применения того или иного метода оценки связи между переменными в зависимости от типа шкалы их измерения (табл. 2.5).
Применение некоторых основных методов статистического анализа в SPSS будет более подробно рассмотрено в следующих подразделах. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что представляют собой таблицы, содержащиеся во вкладках редактора данных SPSS «Свойства переменных» (Variable View) и «Значения переменных» (Data View)? 2. Каким образом осуществляется процедура занесения в исходный файл данных SPSS меток переменных? 3. Чем отличаются пропущенные значения, определяемые системой (system-defined truss, ig values) от пропущенных значений, задаваемых пользователем программы {user-defined missing values)! 4. Какие три типа шкал измерения переменных используются в SPSS и каким образом задается тип шкалы измерения переменной при формировании исходного файла данных? 5. Чем отличаются дихотомическая и категориальная кодировка данных? 6. Почему при занесении в исходный файл данных SPSS ответов ка многовариантные (безальтернативные) вопросы необходимо использовать дихотомическую кодировку данных? 7. С какой целью и в каких случаях применяется двойная запись данных при создании исходного файла SPSS? 8. По шкале какого типа измеряются следующие переменные: а) частота приобретения товара «A» • реже 1-го раза в неделю; • 1—3 раза в неделю; • чаще 3-х раз в неделю; б) семейное положение • замужем/женат; • не замужем/ холост; • разведена/разведен; в) оценка уровня сервисного обслуживания • очень высокая; • высокая; • средняя; • низкая; • очень низкая; г) возраст (23 года, 24 года, 32 года, 57 лет)? 1. Как отличаются друг от друга переменные, измеряемые по разным типам шкал, относительно возможности произведения арифметических операций и расчета статистических показателей? 3. СРАВНЕНИЕ СРЕДНИХ ВЕЛИЧИН В SPSS Методы сравнения средних величин часто используются в маркетинговых исследованиях для выявления взаимосвязи между исследуемыми переменными. К таким методам относятся T-тесты и дисперсионный анализ. В ходе проведения Т-теста или дисперсионного анализа проверяется исходная (нулевая) гипотеза о равенстве сравниваемых средних величин, которая представляет собой утверждение: «Взаимосвязи между исследуемыми величинами не существует». Например, исходная (нулевая) гипотеза предполагает равенство среднего балла успеваемости студентов — юношей и девушек, что свидетельствует о том, что пол студента не влияет на его успеваемость. По результатам проведения анализа данная гипотеза должна быть подтверждена или опровергнута. Основным результатом T-теста или дисперсионного анализа, выдаваемого SPSS, является величина «Significance» («Значимость»). Она характеризует вероятность ошибки, с которой может быть отклонена исходная (нулевая) гипотеза. Если вероятность ошибки мала, исходная гипотеза может быгь отклонена, т.е. ее можно считать неверной (рис. 3.1). Результаты проверки исходной (нулевой) гипотезы определяются доверительным интервалом (Confidence Interval), который задается при формировании задания на проведение Г-теста или дисперсионного анализа в SPSS. По умолчанию устанавливается доверительный интервал 95%. SPSS предоставляет возмож
|

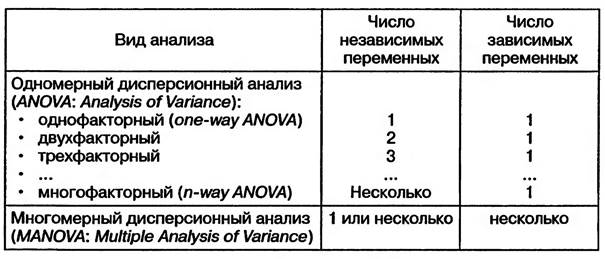
 Рис. 2.1. Редактор данных: вкладка «Свойства переменных» (Variable View)
Рис. 2.1. Редактор данных: вкладка «Свойства переменных» (Variable View)
 Рис. 2.2. Диалоговое окно «Тип переменной»
Рис. 2.2. Диалоговое окно «Тип переменной»


 Рис. 2.5. Редактор данных: вкладка ^Значения переменных» (Data View)
Рис. 2.5. Редактор данных: вкладка ^Значения переменных» (Data View)










