Понятие математического моделирования.
Построение модели начинается с определения параметров и переменных, определяющих процесс функционирования системы. Параметры системы Переменные различают на: зависимые и независимые. Независимые: это входные воздействия (в т.ч. управляющие):
воздействия внешней среды (контролируемые – неконтролируемые, наблюдаемые – ненаблюдаемые и детерминированные – случайные):
состояния системы
Отличаются от θ тем, что характеризуют свойства системы, изменяющиеся во времени. X – пространство состояний или фазовое пространство. Последовательность: x для t1<t2<…<tN называется фазовой траекторией системы. А последовательность y – выходной траекторией. Зависимые: – выходные характеристики (сигналы)
Общая схема функционирования ММ (ММ - математическая модель) системы:
Множество переменных
Если t непрерывно, то модель называется непрерывной, иначе – дискретной (t = i*Δ, i = 1,2,…). Если модель не содержит случайных элементов, то она называется детерминированной, в противном случае – вероятностной (стохастической). Если математическое описание модели слишком сложное и частично или полностью неопределенно, то в этом случае используются агрегативные модели. Сущность агрегативной модели заключается в разбиении системы на конечное число взаимосвязанных частей (подсистем), каждая из которых допускает стандартное математическое описание. Эти подсистемы называются агрегатами.
|
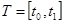- временной интервал моделирования системы S (интервал модельного времени).
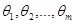- характеристики системы, остающиеся постоянными на всем интервале времени T. Если 
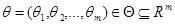, то говорят, что имеется параметрическое семейство систем.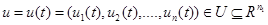
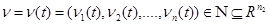
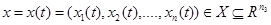
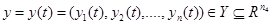
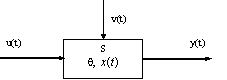
вместе с законами функционирования
и называется математической моделью системы.
